不确定度评价方法在高纯锗探测器参数修正中的应用

李自维，白立新，张一云

(四川大学物理学院，成都 610065)

1 引 言

使用Monte Carlo方法模拟高纯锗探测器对γ光子的探测效率相比传统的物理实验方法能够大大地节约时间和费用[1]，在高纯锗探测器参数标定和修正中有着广泛的应用. 探测器生产厂家给出探测器参数为标称值，而冷指尺寸、真空层厚度等亦未给出，且探测器老化后探测器参数也会变化. 因此根据厂家给出的探测器参数，进行探测效率模拟，得到的结果往往与实验值存在较大的偏差[2]. 为了得到准确模拟结果需要对计算模型的输入参数进行调整. 探测效率由探测器的多个参数共同影响，目前文献中对探测器参数的调整方法还处于人工试探、穷举法等，没有一种理论性强、简便、通用的方法. 本文以计算模型的统计性不确定度评价方法为基础，通过对探测效率的蒙特卡洛计算模型进行敏感性分析和不确定度分析，实现对高纯锗探测器重要参数的修正，在方法上具有通用性和一致性.

2 原理及实验

2.1 高纯锗探测器原理

高纯锗探测器是一种具有高分辨率的半导体核辐射探测器，其用于探测射线的灵敏区域是PN结(又称耗尽层). 当γ射线进入结区时，因γ光子与结区物质发生光电效应，康普顿散射或电子对效应从而损失能量，在结区产生电子-空穴对，在外加反偏电场的作用下，在输出回路中形成能代表入射γ射线能量的输出电信号. 探测器结构如图1所示，高纯锗探测器需要工作在85～100 K的低温环境，来保证锗晶体的禁带宽度.

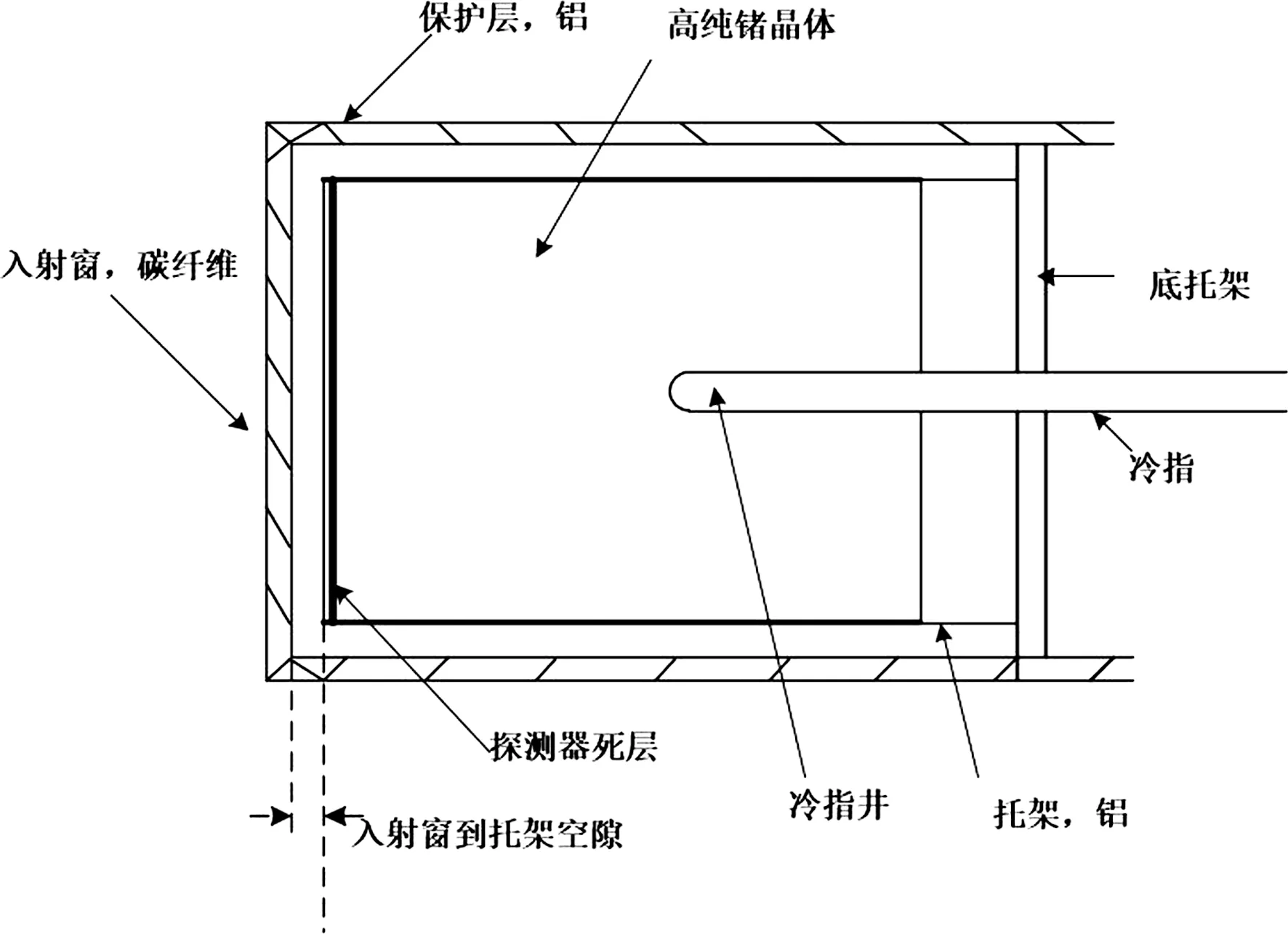
图1 探测器结构示意图Fig.1 Sketch map of HPGe detector

2.2 与探测效率有关的探测器参数

探测效率是探测器的重要指标之一，由多参数共同影响，其准确性直接影响到放射源活度等物理测量结果的准确度[3].

对于特定的放射源和确定的高纯锗探测器，探测效率主要与以下几个探测器参数相关：(1)探测器晶体尺寸，包括晶体半径和晶体高度，探测器灵敏区域的大小主要由晶体的尺寸决定；(2)死层厚度，死层的厚度直接影响探测器晶体的有效体积；(3)冷指尺寸，包括冷指长和冷指半径，入射粒子进入到冷指井中不产生空穴-电子对，冷指的大小也直接影响到探测器晶体的有效体积；(4)空隙高度，入射窗到探测器托架之间的距离称为空隙高度，空隙高度的偏差影响放射源到探测器的距离.

2.3 计算模型的不确定度评价方法

对计算模型的不确定度评价，一般指对计算模型的输出结果与实际值之间的差异进行评价. 包括分析输入参数对输出结果的不确定度贡献和输出参数对输入参数的敏感性.

2.3.1 不确定度评价方法分类和选择 不确定度评价分析方法根据输入不确定度到输出不确定度的传递方向，分为基于输入参数的不确定度传递和基于输出的不确定度传递的不确定度评价分析.

根据对计算模型的输出结果的不确定度计算方法不同，不确定度评价方法分为统计性方法和确定性方法. 目前，基于输入参数不确定度传递的统计性方法的研究和应用相对更为成熟和广泛.

统计性不确定度评价方法首先确定输入参数的分布类型和分布参数，然后对各输入参数抽样生成N个输入样本，用此样本集进行模拟计算得到N个输出集，最后分析输出与输入的关系. 统计性不确定度评价方法是不确定度评价的一种通用方法，示意图如图2所示.

图2 统计性不确定度评价方法Fig.2 Statistical uncertainty evaluation method

探测器效率模拟的模型是一个多输入参数的复杂模型，输出的结果与各输入参数并非简单的线性关系，因此需采用基于输入参数不确定度传递的统计性不确定度评价方法，来分析评价探测器真实效率与模拟效率的关系.

2.3.2 敏感性分析方法 敏感性分析是指分析计算模型的每个输入变量和参数在模型输出变量中的相对重要性[4]. 敏感性分析可用于输入变量和输入参数筛选，输出变量的不确定度分析，减少输出变量不确定度的方法等，其广泛应用于机械、交道运输网络建模、热工水力、电力系统分析和控制以及市场营销、运筹学等领域[5].

敏感性分析分为局部敏感性分析和全局敏感性分析[6]. 局部敏感性分析法关注单个因子对模型输出结果的影响，优点在于简单快捷，可操作性强，但是由于未考虑整个参数空间内的响应，当模型是非线性的或者影响输入变量的不确定度处于不同数量级时，局部技术可能不能够提供有效的分析结果.

全局敏感性分析法分析各因素的概率密度函数的分布和形状的影响，在计算分析时，所有因素都可同时变化[7-8]. 所以，本文采用简相关系数、全局敏感性分析方法Sobol′一阶和总敏感性分析方法对模型输入参数进行敏感性分析.

2.4 不确定评价方法修正参数的原理

在高纯锗探测器对放射源的探测效率模拟中，不确定度的传递示意图如图3所示.探测器的参数是模拟模型的输入参数，探测器参数的不确定度直接反映到模拟的结果中，即模拟效率的不确定度来源于Monte Carlo N-Particle Transport Code，Version 5(MCNP5)程序的模型输入参数(探测器参数)的不确定度.

图3 探测效率模拟中的不确定度传递Fig.3 Uncertainty transfer in detection efficiency simulation process

用模拟程序模拟高纯锗探测器的探测效率，模拟结果与实验效率存在一定偏差，其主要原因是建模的输入参数值与探测器真实参数值的存在偏差. 而输入参数值与真实参数值的偏差程度决定了模拟探测效率与实验效率的偏差程度. 所以，我们认为当模拟探测效率与实验效率偏差最小时，此模型的输入参数与真实参数偏差最小.

本文提出一种不确定度分析法，即对有代表性的多个空间点(对输入参数敏感性高的点)的点源探测效率，采用简单蒙卡抽样方法对重要输入参数的每个参数同时进行N次均匀抽样，使抽样值覆盖探测器真实参数值，由抽样数据生成模拟程序的N个输入卡. 再由探测器效率模拟程序进行N次模拟计算，求出模拟计算结果与真实探测效率的偏差，找出偏差最小值所对应的探测器效率模拟程序输入卡，即可知此最小偏差对应的模拟模型的输入参数，完成探测器参数修正.

2.5 方法验证实验

2.5.1 实验假设和实验目的 本实验合理地假设一组高纯锗探测器参数，作为模拟实验的高纯锗探测器的真实参数. 实验中由这些假设的真实探测器参数作为模型参数模拟计算出的探测效率即认为是真实效率或称为实验效率. 假设另一组高纯锗探测器参数，作为模拟实验的高纯锗探测器的标称值. 由标称值作为模型参数模拟计算出的探测效率称为标称值探测效率.

实验选用137Cs，241Am，60Co做标准γ源，选取9个空间点做为放射源所在位置，这9个点与探测器位置关系如同4所示，第1～9个点位置分别记为位置1，位置2 ,直到位置9.

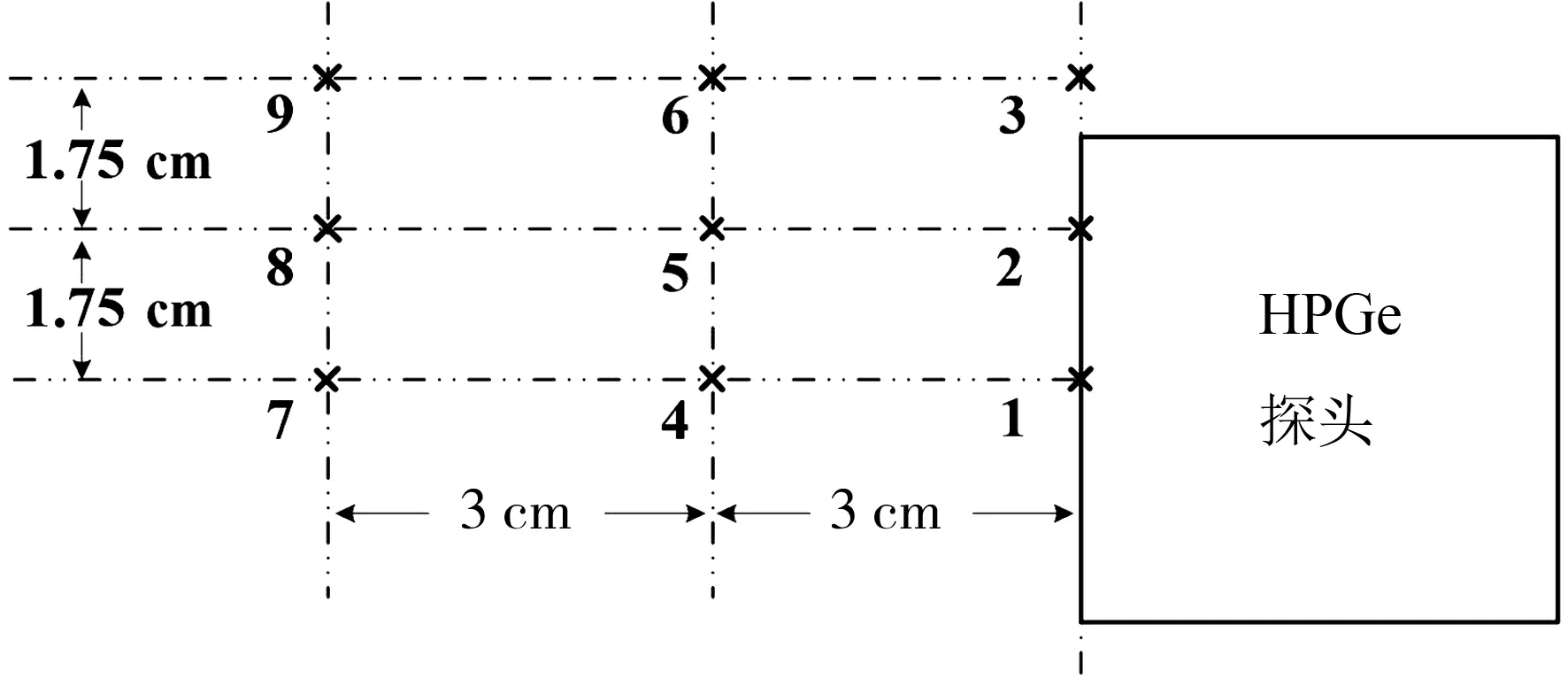
图4 实验选取的空间点Fig.4 Space points in the experiment

实验中，用MCNP5程序模拟高纯锗探测器探测效率，应用前文提出的不确定度评价方法来修正高纯锗探测器参数，最终比较修正的探测器参数与实验假设的探测器真实参数的误差，并验证此不确定度评价方法的正确性.

2.5.2 参数修正 根据前文所提出的不确定度评价方法，对探测器参数进行修正. 第一步，分析高纯锗探测器参数，选取目标参数，分析探测效率对各目标参数的敏感性，确定重要参数.

第二步，对各重要输入参数同时进行N次简单蒙卡抽样，得到N组模型输入参数，根据敏感性分析结果，选取n个标定点，对不同放射源在这n个标定点，用MCNP5程序进行同时的探测器效率模拟，得到模拟计算结果.

第三步，计算探测器对各空间点对应放射源的真实探测效率与模拟效率的偏差的平方之和，表示为ΔEff.

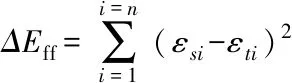
其中，εsi表示模拟效率，εti表示真实效率.找到最小ΔEff，这个ΔEff对应的那组模型参数值即可认为是最佳参数值，也就是探测器参数的修正值.

本实验采用针对多个有代表性的空间点，对不同的放射源进行同时的探测器效率模拟，是因为探测器探测效率是由多参数共同影响的，在进行探测器对确定位置的单一放射源进行探测效率模拟时，容易出现多个模型输入参数均与真实值偏移较大，而模拟效率却接近真实效率的情况. 而采用多空间点多放射源进行同时模拟，能很好地避免这种情况.

2.5.3 参数验证 根据修正的高纯锗探测器参数，令137Cs，241Am，60Co这3个γ放射位于除标定点外的其他m个点，用MCNP5程序模拟探测器对其探测效率，并与用实验假设的探测器真实参数模拟计算的探测效率进行对比，以此检验探测器参数的修正结果.

2.6 探测效率的MCNP程序模拟[9]

本文采用Monte Carlo光子和电子耦合输运程序MCNP5对高纯锗探测器探测效率进行模拟.MCNP程序是一款应用广泛[10]，由Los Alamos国家实验室研发的基于蒙特卡罗方法的大型的多功能Monte Carlo粒子输运程序. 该程序目前可用于计算与中子、光子和电子或耦合中子、 光子、 电子相关的物理输运问题[11].

在光子和电子的耦合输运过程中，模拟计算的光子能量为1 keV～100 MeV，适合于γ射线的模拟计算[12]. 在探测效率模拟中，用脉冲幅度卡F8计算γ射线在HPGe晶体中的脉冲高度能谱分布，联合使用E8计数卡，即可求得探测器的模拟效率.

2.7 敏感性分析

2.7.1 确定输入参数及参数抽样 分析影响探测效率的模型参数，选取探测器晶体半径，空隙高度，死层厚度，冷指半径，冷指长度，晶体高度共6个输入参数作为进行敏感性分析的目标参数.

各输入参数的相对偏差并无严格的统计数据指导. 一般由标称值模拟的探测效率与真实效率相对误差在20%以上，因此可由MCNP5程序模拟计算出探测器参数的最大偏移量. 结合实验室经验数据，假设各输入参数的分布均服从正态分布，得到各参数的标准差，如表1所示.

采用拉丁超立方抽样方法对输入参数进行N次同时抽样产生N个输入样本，并保存抽样结果.

表1 输入参数分布Tab.1 The distribution of input parameters

2.7.2 模型计算及敏感性计算 由抽样数据编写N个MCNP5程序的输入卡，由自编程序调用MCNP5程序进行模拟计算，保存目标参数. 这里目标参数只有一个，即模型计算的结果模拟探测效率.

根据抽样时保存的输入参数抽样结果和模拟计算得到的探测器效率，先后计算各输入参数的简相关系数、Sobol′一阶敏感系数和Sobol′总敏感系数.

3 敏感性分析及参数修正

3.1 敏感性分析结果

选取位置2，位置4，位置5，位置8，位置9放置不同放射源做敏感性分析. 首先，对6个输入参数分别抽样500、1 000、2 000、3 000次，令137Cs放射源处于位置4，用MCNP5程序进行探测效率模拟，计算出简相关系数，Sobol′一阶敏感系数和Sobol′总敏感系数. 当抽样数是2 000次时，各个参数的敏感性计算结果与1 000次抽样的计算结果偏差在5%之内，3 000次抽样计算结果与2 000次抽样的计算结果偏差在2%之内，故此认为当抽样数为3 000时，敏感性分析结果收敛. 下文敏感性分析结果均为抽样3 000次时的数据.

这里列出137Cs源位于位置3、241Am源位于位置5，60Co源位于位置6的敏感性分析结果，如表2所示.

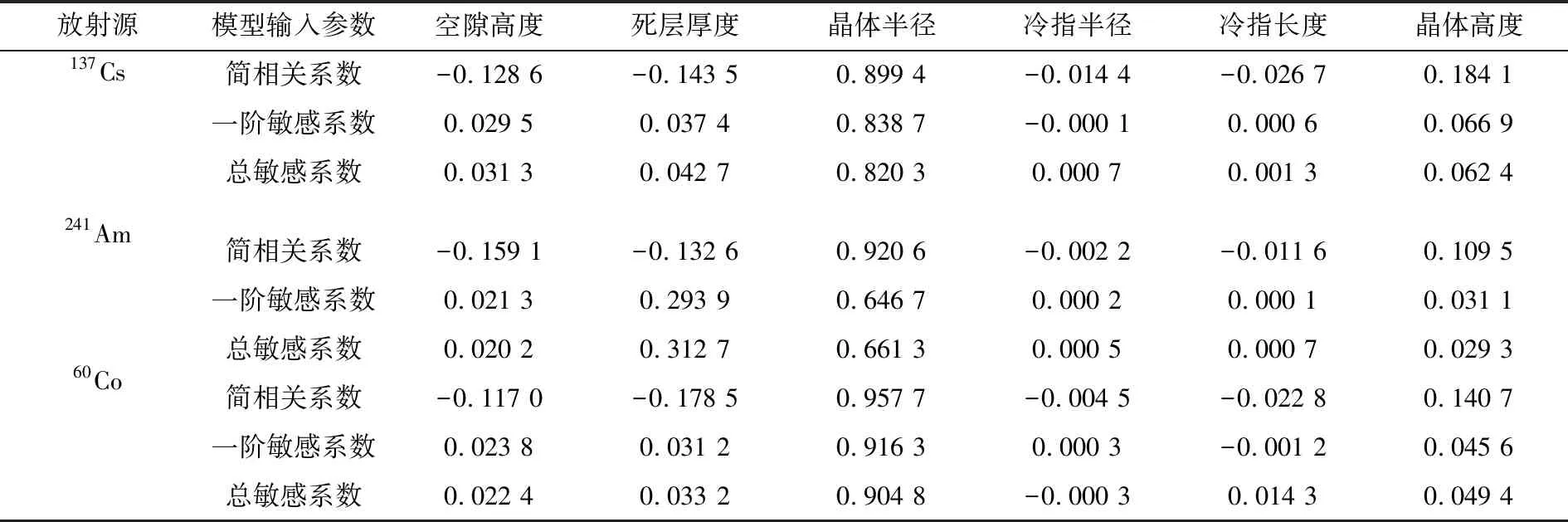
表2 敏感性分析结果Tab.2 The results of sensitivity analysis

由结果可见相关系数和Sobol′敏感系数具有一致性，这证明了在MCNP5程序模拟探测器效率中应用Sobol′敏感性分析的正确性. 结果表明，模拟探测效率对探测器参数的敏感度与放射源位置和入射γ光子能量均有关系：当入射粒子能量低时，探测效率对死层厚度较为敏感，而入射粒子能量高，且放射源位置不在探测器晶体轴向时，探测效率对晶体半径、高度敏感度比较大.

综合分析不同放射源在其他位置的敏感性研究结果，高纯锗探测器探测效率对死层厚度、晶体半径、晶体高度这3个探测器参数的敏感性始终大于对冷指半径、冷指长和空隙高度这3个参数的敏感性，且当放射源偏离轴心时，探测效率对晶体高度更敏感. 因此，晶体的半径和死层厚度应该作为探测器重要参数. 高纯锗探测器探测效率对冷指长度和冷指半径敏感性很小，所以冷指长度和冷指半径不作为重要参数.

3.2 模型参数修正

3.2.1 寻找最佳模型参数 根据敏感性分析的结果，选取晶体高度、晶体半径，死层厚度这三个重要参数进行修正，用于参数修正的标定点应该选偏离轴心的点.

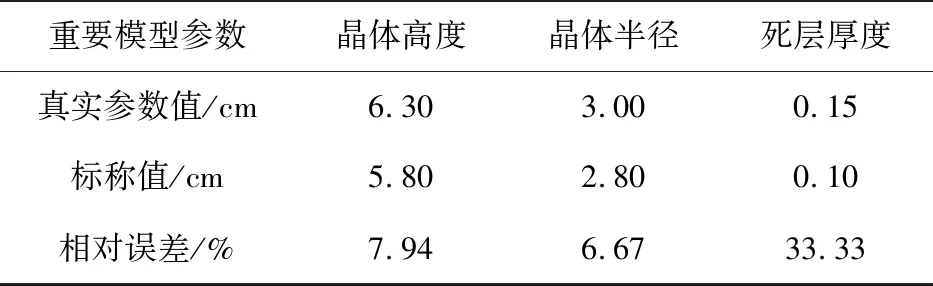
表3 重要模型参数值Tab.3 Important model parameter values

选取位置3，位置5，位置6作为标定点，修正参数所用γ放射源仍为241Am，60Co，137Cs.241Am源在位置3，137Cs源在位置5，60Co源在位置6. 对这三个位置的点源，用MCNP5程序模拟高纯锗探测器对他们的探测效率. 实验所假设的探测器重要参数真实值与标称值如表3所示.

经MCNP5程序模拟计算的探测器对各放射源的真实探测效率和使用标称值计算的模拟效率结果如表4所示.

表4 不同γ源在不同位置的探测器探测效率Tab.4 The detection efficiencies for different γ sources located at different spatial points

采用简单蒙卡抽样方法对晶体高度、晶体半径死层厚度共3个输入参数，同时进行均匀抽样3 000次，生成3 000张MCNP5程序输入卡并进行模拟计算.

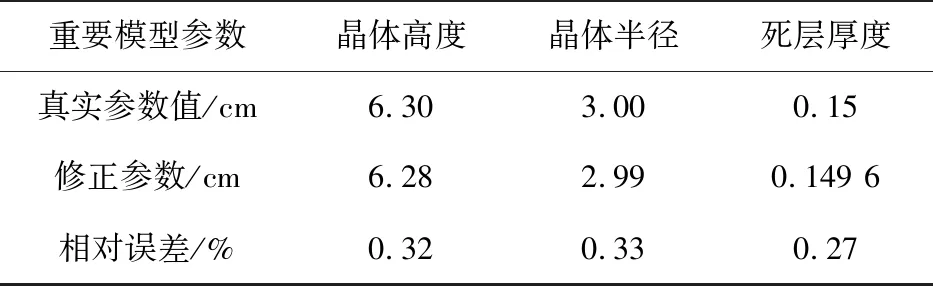
表5 探测器参数修正结果Tab.5 The results of corrected important detector parameter values

求出3个γ源在3个不同位置的模拟探测效率与真实探测效率的偏差的平方和ΔEff，并找出最小值，得出对应输入参数的值. 这些参数值即视为探测器参数的修正值，修正值如表5所示. 结果表明，修正的探测器参数非常接近真实值，各个参数与真实值的相对误差均在0.5%内. 采用修正后的探测器参数建模计算高纯锗探测器对不同γ点源在3个标定位置的探测效率，结果如表6所示，模拟探测效率与真实的探测效率相对误差均在0.5%之内.

表6 参数修正后的探测器探测效率Tab.6 The detection efficiencies after parameters corrected

重复上述参数修正步骤12次，共有11次修正得到重要参数的修正值与真实值相对误差均未超过2%. 有1次探测器参数修正值与真实值相对误差在10%左右，而模拟效率与真实效率相对误差在1%内. 这是前文所提到的修正的偶然性. 对于这种修正结果直接舍弃.

3.2.2 修正参数验证 选取位置2，4，8作为验证点，采用修正后的探测器参数，使用MCNP5程序建模分别计算137Cs，60Co，241Am放射源处在验证点的探测器探测效率，以此验证探测器重要参数修正是否正确. 对各源，高纯锗探测器的探测效率真实值与模拟的探测效率结果如表7所示.

结果表明，使用修正后的探测器参数对不同点源在验证点进行探测效率模拟，结果与真实效率相对误差均在0.5%之内，这远好于传统修正方法修正的结果(传统修正方法的修正结果一般相对误差在2%～5%之内).这很好地说明了应用此方法修正探测器重要参数的正确性和准确性.

表7 探测器对验证源的探测效率Tab.7 The detection efficiencies for verification sources

4 结 论

使用MCNP5程序能快速地模拟高纯锗探测器的探测效率，节约实验成本，缩短实验时间. 应用本文提出的不确定度分析方法来辅助标定或修正探测器参数，修正后的探测器参数与真实探测器参数相对误差在2%以内.此方法具有良好的重复性，参数修正效果好于传统的高纯锗探测器参数修正方法. 此方法同样也适用于其他类型的核探测的探测器参数标定与修正.

不确定评价方法在具有多输入参数且复杂的模型计算的热工水力、机械结构、电力输运等工程领域已经有广泛的应用和研究[13].在实验室领域，对于较为简单的计算模型，应用不确定度分析的思想，应用统计性不确定度评价方法来分析输入参数或模型参数与输出目标参数的关系也是实用且便捷的.