含阻尼项的SRLW方程的一个去耦合线性化差分格式

魏 杰，何 丽，胡劲松

(西华大学理学院，成都 610039)

1 引 言

本文考虑如下带有阻尼项的耗散SRLW方程的初边值问题：

uxxt-ut+υuxx=ρx+uux，

(x,t)∈(xL,xR)×(0,T]

(1)

ρt+ux+γρ=0，

(x,t)∈(xL,xR)×(0,T]

(2)

u(x,0)=u0(x)，ρ(x,0)=ρ0(x)，

x∈[xL,xR]

(3)

u(xL,t)=u(xR,t)=0，

ρ(xL,t)=ρ(xR,t)=0，t∈[0,T]

(4)

其中υ>0是耗散系数，γ>0是阻尼系数；u0(x)、ρ0(x)是已知函数.当考虑耗散时，方程组(1)-(2)是反映非线性离子声波运动本质现象的合理模型[1].

文献[2-5]分别讨论了方程组(1)-(2)周期边值问题和初边值问题的解的适定性、整体存在唯一性及其解的长时间性态等.文献[6]用有限元方法对问题(1)～(4)进行了数值研究.文献[7-8]对问题(1)～(4)进行了有限差分方法研究.文献[9-11]又进一步对带有阻尼项的广义SRLW方程进行了有限差分方法研究，但所提出的都是耦合差分格式，计算量一般都比较大.

本文利用外推技巧，在保持二阶理论精度的前提下对初边值问题(1)～(4)提出一个非耦合的三层线性差分格式.该格式在数值求解时只需对函数u和ρ分别单独求解，其中对函数u的数值求解为线性化差分算法，对函数ρ的数值求解为显式差分算法，大大提高了数值求解效率.当不能得到其差分解的最大模估计时，本文综合运用数学归纳法和离散泛函分析方法直接证明了格式的收敛性和稳定性，并给出数值算例.

2 差分格式及截断误差

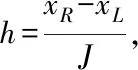
j=0，1,…,J-1,J}.

对初边值问题(1)～(4)考虑如下有限差分格式：

j=1,2,…,J-1；n=1,2,…,N-1

(5)

j=1,2,…,J-1；n=1,2,…,N-1

(6)

(7)

(8)

差分格式(5)～(8)的截断误差定义如下：

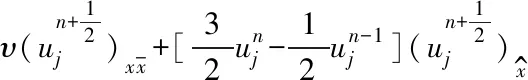
(9)

(10)

由Taylor展开可知，当h,τ→0时

(11)

3 差分格式的收敛性和稳定性

引理3.1[7-8]设u0∈H1，ρ0∈L2.初边值问题(1)～(4)的解满足

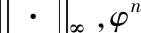
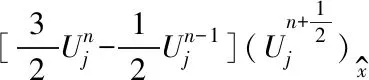
(12)

(13)

由引理3.1以及(11)式知，存在与τ和h无关的常数Cu，Cr和Cs，使得

Cs(τ2+h2)，n=1,2,…,N

(14)

由初始条件(7)式可得到估计式

(15)

再由两层二阶差分格式[8]计算出U1和φ1即可得到以下估计式：

(16)

这里C1为与τ和h无关的常数.现在假设

l=2,3,…,n，n≤N-1

(17)

其中Cl(l=2,3,…,n)为与τ和h无关的常数.则由离散Sobolev不等式[2]和Cauchy-Schwarz不等式有

(18)

h2)，l=1,2,…,n

(19)

(20)

(21)

由引理3.1以及微分中值定理，有

(22)

再取h和τ充分小，使

(23)

于是由(19)、(22)式和(23)式以及Cauchy-Schwarz不等式有

(24)

(25)

(26)

(27)

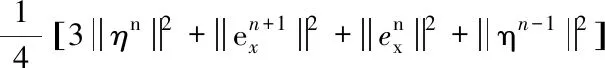
(28)

(29)

将(20)与(21)式相加，并将(24)～(29)式代入后整理得

(30)

将(30)式从1到n递推求和，整理得

(31)

由(14)式有

T(Cr)2(τ2+h2)2

(32)

T(Cs)2(τ2+h2)2

(33)

再将(16)、(32)、(33)式代入(31)式，利用离散Gronwall不等式[12]，取时间步长τ充分小以满足

于是有

(τ2+h2)2e2T[12(Cu+1)]≤

(Cn+1)2(τ2+h2)2，n=1,2,…,N-1，

其中

显然Cn+1为与n无关的常数.从而由归纳假设有

最后由离散Sobolev不等式[13]有

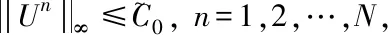
4 数值实验

(5)式和(6)式可改写为如下形式：

(34)

(35)

其中

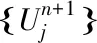
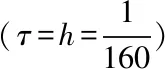
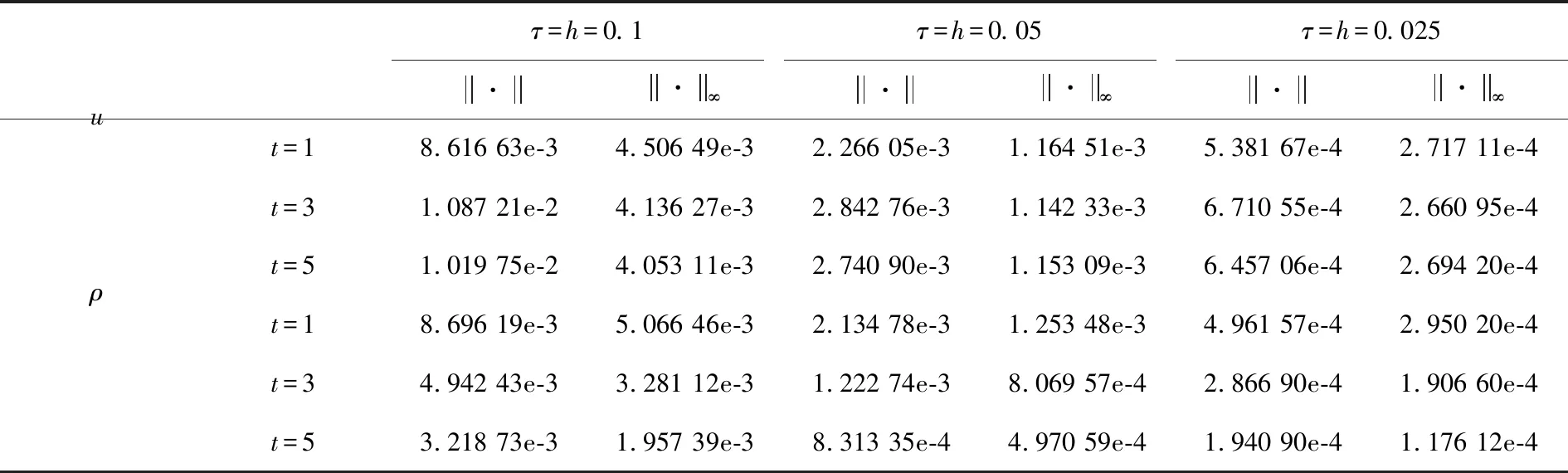
表1 差分格式在不同时刻的误差Tab.1 The error of the difference scheme at various time

5 结 论

数值结果表明，本文对问题(1)～(4)提出的差分格式(5)～(8)是有效的，明显具有二阶精度.该格式解除了方程组(1)、(2)中函数u和ρ的耦合关系，且实质上是一个半显式线性差分格式，相对于其他耦合的差分格式，其计算时间更加节省、求解效率更高.