铜在铍晶体中扩散系数和浓度分布的理论研究

曹华亮，程新路

(四川大学原子与分子物理研究所，成都 610065)

1 引 言

铍是聚变反应中的第一壁材料[1-2]，同样被考虑用作惯性约束聚变候选材料，其具有很多优点，如高密度、低不透明性、高熔点和高热导等性质[3-4]. 这些性质使得铍具有很高的烧蚀速率，在间接驱动惯性约束聚变实验中非常有利于提高内爆耦合效率，而且能够有效抑制烧蚀不稳定性增长[5-8]. 为了增加铍靶丸的内爆稳定性和改善其对X射线的吸收，梯度铜掺杂铍靶丸在实验中被广泛使用[8-13]. 图1是一种铍铜靶丸的结构示意图，其中铜原子按一定梯度进行掺杂.

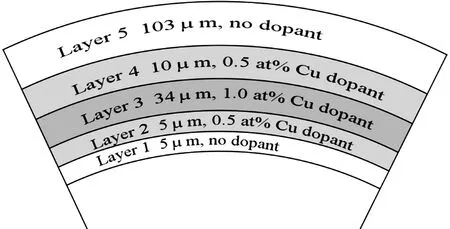
图1 五层梯度铜掺杂靶丸示意图Fig.1 Five-layer gradient copper-doped capsule

铜原子可以阻止X射线对燃料的预热、抑制瑞利-泰勒(Rayleigh-Taylor)不稳定性的增长[4，14]还能帮助控制冲击时间[15]. Huang等人[16]通过实验研究发现，靶丸在698 K热解48 h后Layer 2和Layer 4中铜原子扩散长度分别为6m和3m，这远大于与Butrymowicz等人[17]给出的实验结果；同时也发现铜原子在铍晶体中的扩散沿不同方位角和径向都是不均匀的，这种扩散使得靶丸在内爆的过程中产生瑞利-泰勒不稳定性，严重降低了靶丸的内爆性能[18]. 为了防止铜原子在靶丸中的扩散，Youngblood等人[15]使用原子层沉积(atomic layer deposition：ALD)的方法制备出了厚度约1～8 nm的氧化铝阻挡层，在靶丸热解后发现氧化铝层可以有效地阻挡铜原子的扩散，但发现梯度掺杂层界面出现了分层的现象，目前并不清楚界面的分层是靶丸制备过程还是检测过程中产生的. Xu等人[18]在靶丸梯度掺杂层界面掺杂氧原子发现也可以有效阻挡铜扩散，但遗憾的是氧原子层也使得界面分层且产生了很大的空隙. 因此研究铜原子在铍晶体中的扩散是很重要的.

目前还没有学者对铜在铍晶体中扩散系数研究进行过报道. 分子动力学方法是一种很好的模拟材料性质的方法[19-20]，本文使用这种方法计算了铜原子在铍晶体中的扩散系数，并分析了铜原子扩散浓度与深度的关系.

2 计算方法

本文使用分子动力学方法研究了铜在铍晶体中的扩散行为，模拟过程中首先计算出铜原子的均方位移(MSD)，然后使用Einstein-Smoluchowski关系得到扩散系数D.

(1)

(2)

其中MSD(t)是原子从0时刻所处的位置ri(0)到t时刻所处的位置ri(t)过程中均方位移的平均值，d是体系的维数，N是掺杂Cu原子个数. 通过对不同温度条件下铜原子均方位移的拟合获得铜原子扩散系数D.

阿伦尼乌兹(Arrhenius)扩散方程：

(3)

使用该方程拟合得到的扩散系数可以获得相应条件下的扩散方程，其中D是扩散系数，D0是置前因子，E是扩散激活能，R是理想气体常数，T是绝对温度. 得到扩散系数后根据菲克第二定律求解铜原子浓度C(x,t)，当溶质原子是面源时C(x,t)的解为[21]：

(4)

其中M是溶质原子的总物质量，D是扩散系数，x是扩散深度，t是扩散时间. 图2是铍铜靶丸梯度界面模型示意图，以此为边界条件结合方程(4)可以求解得到铜原子浓度与扩散深度的关系：

C=0x<-L

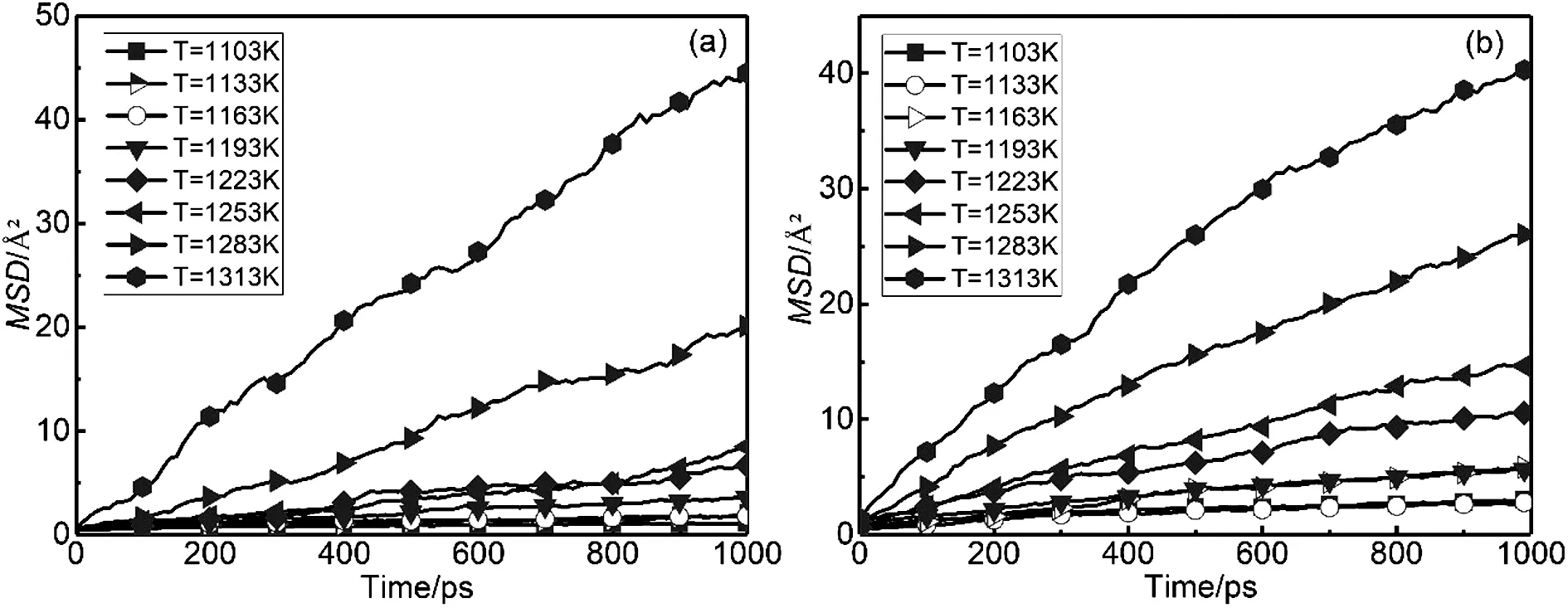
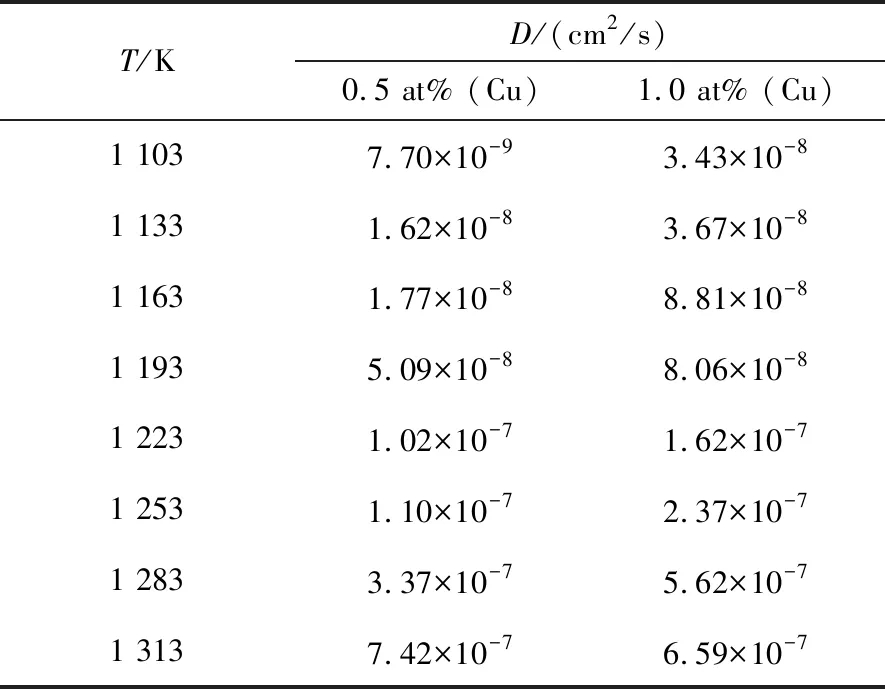
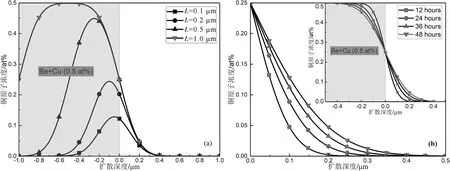
C=C0-L

C=0x>0

(5)

其中C0是铜原子掺杂浓度，L是铜掺杂层厚度，x是铜扩散深度.

模拟过程中使用程序是LAMMPS，原子间相互作用势采用混合相互作用势函数，其中铍原子间采用Agrawal等人[22]提出的铍嵌入原子势函数(EAM)，这个势函数相比之前的EAM和MEAM更精确，其对HCP结构晶格常数和结合能的预测值与实验误差小于1.0%；铜原子间采用Foiles等人[23]提出的嵌入原子势函数，铍铜原子间采用Sharma等人[24]提出的铍铜Morse势函数.

图2 铍铜靶丸梯度界面示意图Fig.2 Schematic of the gradient interface of the capsule

3 计算结果和讨论

3.1 铜原子扩散系数计算

模拟过程中使用LAMMPS建立了67.6 Å×117.2 Å×110.5 Å的铍晶体模型，共包含97 556个原子，铜原子以替换方式进行掺杂，浓度分别为0.5 at%和1.0 at%. 模拟过程中时间步长设置1 fs，升温速率为10 K/ps，体系升温和弛豫过程中使用NPT系综. 升温时首先给弛豫后的体系设定1 K的初始温度并弛豫5 ps，然后采用程序升温的方法将体系升温至设定温度，最后对已达到设定温度的体系继续弛豫100 ps，这样做的目的是为了保证在计算均方位移之前体系被充分平衡. 由于体系弛豫之后已充分平衡，因此在最后计算铜原子均方位移时使用NVT系综，此阶段模拟时间1 ns. 如图3所示，通过分子动力学模拟得到了铜原子的均方位移. 使用公式(2)拟合均方位移后获得铜原子扩散系数D，拟合结果如表1所示.

图3 不同铜掺杂浓度时各温度条件下铜原子均方位移:(a)铜掺杂浓度0.5 at%;(b)铜掺杂浓度1.0 at%Fig.3 The mean square displacement of copper atoms under different temperature conditions: (a) the concentration of copper-doped is 0.5 at%; (b) the concentration of copper-doped is 1.0 at%

表1 铜原子扩散系数Tab.1 The diffusion coefficient D of copper in beryllium crystals

根据表1得到的扩散系数结合公式(3)拟合出两个铜掺杂浓度条件下的扩散激活能E和置前因子D0，若假设低温区域的扩散激活能和置前因子与高温一致则可以使用拟合得到的扩散方程对相应温度条件下铜原子的扩散系数进行预测. 拟合结果如下：

DCu_0.5at%=6.63×103exp(-60 665 cal·

mol-1/RT)cm2/s

(6)

DCu_1.0at%=4.39exp(-41 452 cal·mol-1/

RT)cm2/s

(7)

美国劳伦斯里弗莫尔国家实验室的Huang等人[16]的实验中铍铜靶丸热解条件是698 K保持48 h，对热解之后的靶丸做背散射电子成像(BSE)后发现铜原子在铍晶体中的扩散距离约为3～6m，根据扩散方程计算后发现热解过程中铜原子的扩散系数约5.2×10-13cm2/s至2.1×10-12cm2/s. Butrymowicz等人给出了铜原子在铍晶体中扩散系数的实验数据，通过对数据的拟合得出铜原子在铍晶体中的扩散方程为[17]：

DBasalplane=0.35exp(-45 900 /RT) cm2/s

(8)

Dc_axix=0.90exp(-49 500 /RT) cm2/s

(9)

如图4所示，将本文模拟得到的扩散系数与Huang和Butrymowicz等人报道的结果进行了对比. 当温度为698 K时根据公式(7)发现铜扩散系数为4.66×10-13cm2/s，这与Huang等人的实验结果符合得很好；根据公式(6)得到的铜原子扩散系数与Butrymowicz等人的结果相符. 这说明铜原子掺杂浓度是影响其扩散的一个重要因素.

图4 铜在铍晶体中的扩散系数Fig.4 The diffusion coefficient of copper in the crystal of beryllium

3.2 铜原子扩散浓度与深度分析

Huang等人通过实验发现当铜原子掺杂浓度为1.0 at%时在热解之前并没有向未掺杂铜原子一侧扩散，热解之后在未掺杂铜原子的铍晶体中深度5m处铜扩散浓度约为0.06 at%[16]. 将铜掺杂1.0 at%温度698 K时计算得到的铜原子扩散系数(4.66×10-13cm2/s)代入公式(5)得到铜原子扩散浓度与深度的关系. 如图5(a)所示，当铜掺杂层厚度L为5、 10和100m时其在698 K热解48 h的浓度分布曲线. 当扩散深度为6.2m时铜原子浓度为0.06 at%，这与Huang等人[16]实验中给出的结果相近(x=5m ，Cu 0.06 at%)，当铜掺杂层厚度L大于10m时其在Be晶体中的浓度分布曲线几乎不变(T=698 K，t=48 h). 当铜原子扩散深度为10m时其浓度为0.006 3 at%，这说明此时靶丸Layer 3中铜原子对Layer 5中扩散的铜原子几乎没有贡献. 如图5(b)所示，我们给出了4个不同热解时间(t=12、 24、 36、 48 h)时铜原子的浓度分布曲线(L=10m，T=698 K)，当t=36 h时铜原子的扩散深度(T=698 K、x=5.4m、Cu 0.06 at%)与Huang等人的实验结果最为接近. 如图6(a)所示，使用同样的方法求解铜掺杂浓度为0.5 at%时其扩散浓度与深度的关系，当铜掺杂层厚度L大于1m时铜原子在Be晶体中的浓度分布几乎不变(T=698 K，t=48 h). 在图6(b)中我们给出了不同热解时间条件下铜原子浓度分布曲线，发现当扩散深度为0.2m时铜原子浓度小于0.05 at%(L=1m，T=698 K，t=48 h)，这说明此时铜原子向铍晶体中的扩散几乎可以忽略. 又因在靶丸热解过程中Layer 3中的铜原子扩散深度为10m时的浓度仅为0.006 3 at%，所以若在靶丸的设计中将低浓度(0.5 at%)铜掺杂层厚度增大至10m则可以降低铜原子向铍晶体中扩散的深度，从而提高靶丸在内爆过程中的稳定性.

图5 (a)不同厚度的铜掺杂层在热解后铜原子扩散浓度曲线(T=698 K); (b)铜原子扩散浓度与时间的关系(T=698 K，L=10 m)Fig.5 (a)Copper atom diffusion concentration profile after pyrolysis of copper-doped layers of different thicknesses; (b) the effect of diffusion time on the diffusion concentration distribution (T=698 K，L=10 m)

图6 (a)不同厚度的铜掺杂层在热解后铜原子扩散浓度曲线(T=698 K); (b)铜原子扩散浓度与时间的关系(T=698 K，L=1 m)Fig.6 (a) Copper atom diffusion concentration profile after pyrolysis of copper-doped layers of different thicknesses; (b) the effect of diffusion time on the diffusion concentration distribution(T=698 K，L=1 m)

4 结 论

本文使用经典分子动力学方法研究了铜在铍晶体中的扩散系数，并分析了铜原子扩散浓度和深度之间的关系. 研究表明：当铜掺杂浓度为1.0 at%温度为698 K时铜原子的扩散系数与美国劳伦斯里弗莫尔国家实验室的实验结果符合的很好，铜掺杂浓度为0.5 at%时扩散系数的计算结果与铜掺杂浓度1.0 at%时差别较大，由此推测铜原子在铍晶体中的掺杂浓度是影响其扩散的一个重要因素. 其次，在698 K时对体系热解后铜原子在铍晶体中扩散浓度和深度进行分析(Cu 1.0 at%)，发现铜原子在铍晶体中扩散深度为10m时其浓度为0.006 3 at%，这几乎可以忽略；当铜掺杂浓度为0.5 at%经过48 h的热解后并未发现铜原子有明显的扩散. 因此若在靶丸制备过程中增大Layer 2厚度，则可以在靶丸热解时降低Layer 3中铜原子向Layer 1中扩散的深度. 这对制备性能更高的靶丸是非常有用的.