一种预测判断蛋白质DNA相互作用位点的新方法

王皆恒，李 校

(四川大学生命科学学院 四川省分子生物与生物技术重点实验室，成都610064)

1 引 言

对生命活动起到关键作用的两类生物大分子就是蛋白质和DNA.而这二者之间的相互作用则是大量生理生化反应的核心，它在基因表达调控[1]、组蛋白修饰[2]，DNA复制、修复和重组[3]等细胞过程中发挥着极其重要的作用.蛋白质中有一类序列被称为“功能残基”，它们只占庞大的功能蛋白质序列中的一小部分，但却真正的参与了与其他生物大分子的相互作用以及各类生理生化反应.也正因如此解析这类“功能残基”的真正功能和作用位点变得极为关键.例如：如果想要深入地了解转录过程的机理，不可避免地需要首先了解转录过程中的DNA相互作用位点.关于蛋白质功能残基位点的寻找主要有两种方法：第一种方法即为传统的通过位点突变来确定蛋白质功能残基的实验方法，实验方法的准确率较高但需要大量人力物力的投入，同时实验周期较长，完全无法满足目前生物学数据的增长速度.由于蛋白质的序列结构和功能之间有着紧密的联系，若两种蛋白质的功能残基序列或结构相似，那么从生物意义上来讲这二者很有可能存在相似的生物学功能，因此仅仅通过单纯的数据计算也可以预测得到有意义的功能预测结果.

随着基因组/转录组测序技术的不断发展和成本不断降低，大量的生物学数据也需要这样一种高效的方法快速筛选需要的生物学数据，进而快速而精准的预测蛋白质上的功能残基位点.

在蛋白质转移至靶细胞形式功能的过程中，蛋白质的部分基团承载着前往靶细胞的定位信息，通过这些基团内的信息寻找靶细胞相关相互作用位点的过程也被称之为亚细胞定位[4].在亚细胞定位信息领域，通过支持向量机(SVM)进行亚细胞定位分析已经取得显著成果.同时，支持向量机也可以对蛋白质中简单的四种超二级结构进行预测[5].经过改进的Weighted SVM[6]对于蛋白质磷酸化位点也有着不错的预测效果.而多重支持向量机首尾相连进行大量特种归类也被称为神经网络算法[7].生物信息学分析着眼于序列比对、结构预测、分子进化等领域[8]，随着数据量的增加神经网络算法势必能够为其他更深入的科学工作提供更可靠的实验数据分析.

日前，在PDB数据库[9]中储存的蛋白质-DNA复合体三维结构数据日益增加，这些结构数据也为功能残基位点预测提供了大量的数据来源.在生物信息学中我们可以在这些数据库中挖掘提炼已有数据，对其进行不同特点和功能的分类和统计分析，从而得到潜在的结构或者序列共同点，并以此为基础整理成自动化算法对未知蛋白的功能残基位点进行预测.在本论文当中我们共设计了两种预测蛋白质功能残基的计算方法：基于相似序列的一级结构预测、基于机器学习算法的支持向量机(SVM)预测.并对其结果进行归一化整合，得到最佳的预测结果.

2 材料与方法

2.1 数据集构建

我们使用了PDNA_62和PDNA_224数据集来评估我们的预测能力，两个数据集的来源如下：

PDNA_62：PDNA_62是一个由Ahma and Sarai建立的经典非冗余蛋白质-DNA复合物数据集[10]，主要集中了Protein Data Bank (PDB)[9]数据库中分辨率高于3.5 Å的蛋白质-DNA复合物，并去除序列相似度高于25%的冗余序列.PDNA_62数据集中共包含1 215个DNA相互作用位点，以及6 948个非DNA相互作用位点.

PDNA_224：根据最新版本的PDB数据库(2019年7月4日)，检索DNA结合蛋白，并将X晶体衍射分辨率设置为3.0 Å，这样从数据库里面得到978个蛋白质-DNA复合物.利用PISCES software过滤[11]对候选复合物序列进行过滤，并剔除相似度高于25%的冗余序列，再去除与PDNA_62中的同源序列，最终得到224条非冗余蛋白质序列.其中共包含3 778个DNA相互作用位点和53 570个非DNA相互作用位点.

2.2 基于SVM的预测器

由于蛋白质中每个残基的特征可以用一个读码窗来描述，读码窗由中心残基(central residue)及其n个相邻残基的位置组合而成，若相邻残基不存在，则用0来表示.假设读码窗的长度取L，每个中心残基拥有P=24个特征数，那么预测蛋白质-DNA相互作用位点的特征总数是L×P=L×24，最后将这些特征量格式化为支持向量机的输入数据，得到预测结果.我们所利用的是公用的LibSVM软件，该软件从http://www.csie.nut.edu.tw/～cjlin/libsvm[12]下载得到.LibSVM将其输出结果转化成条件概率通过使sigmoid函数，sigmoid函数的定义如下：

其中x是支持向量机的输入特征，sdv(x)代表输入特征x的阈值，P(Y=1|x)是条件概率结果，A和B分别是sigmoid函数的斜率和偏移参数.官方文档推荐A=-2.0，B=-0.5.此外，由于我们的数据集中正负样本差异过大，因此我们使用了随机过抽样(over-sampling)分析，并使用LibSVM的RBF(radial basis function)内核进行超平面分类器进行建模，以期尽可能消除样本数量对SVM带来的偏差.

为了是其预测结果能够更好地与后续序列匹配预测器结果整合，我们将上述方程进行反函数处理，使最终结果为SVM预测阈值.

2.3 基于序列匹配的预测器

PDNA_62和PDNA_224中的序列文件保存为FASTA格式，但其并不能很好地反映序列之间的替换关系.因此利用PSI-BLAST，根据BLOSUM62替代矩阵对数据库进行初始化打分，生成PSSM蛋白质特征矩阵(图1).

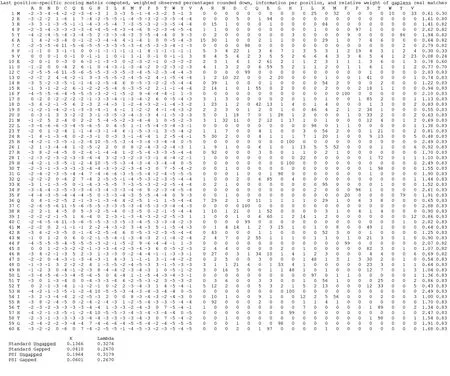
图1 蛋白质1TC3中C段肽链的PSSM特征矩阵Fig.1 PSSM matrix of C-chain in protein 1TC3

使用初始化后的PSSM数据文件进行计算.序列的提取与SVM中的信息窗口类似，使用一个长度为n的读码框(n=3、5、7、9、11……)，若两边数据不足则用0补齐.读码框在已知(B)和未知(A)序列中同时滑动，并在相应位点进行计算.相应的计算公式我们使用了锌指结构预测中CHDEs氨基酸得分的计算公式[13].

Score(α,β)=

此公示中α,β表示两条序列，j表示长度为n的读码框中第j位点的匹配的分，i则表示每个位点的氨基酸与20个标准氨基酸进行匹配，αni、βni则表示这些氨基酸的匹配的分，关于单个位点与20个氨基酸得分对应关系，依旧沿用BLOSUM62氨基酸得分矩阵，具体的计算方法如下.Pi则代表氨基酸i出现的背景频率.最终将所有读码框的得分相加，总得分即能够代表功能未知序列(A)和功能已知序列(B)之间的相似关系.

αi,j=eMi,jλupi

其中Mi,j即为BLOSUM62矩阵中两氨基酸对应得分，λμ即为PSSM格式化后的α文件中standard ungapped Lambda value.

由于此方法得到大量得分结果，最理想的情况中，我们希望这些整理后的坐标呈强烈的线性关系，这样才能够进一步说明两个片段之间拥有强烈的相关性.因此我们以单个蛋白质肽链前x%、整个训练集得分的第y%作为阈值，由于皮尔逊系数可以用来表示坐标点的相关性，因此我们使用皮尔逊相关性约束作为参数，同时调整窗口长度(n=7,9,11,……)，建立模型进行训练，并使用训练结果最优的模型进行得分筛选，得到初步的待处理匹配位置，并将匹配位置整理成坐标形式.筛选模型可分为四类：

type1：用单个蛋白质肽链前x%最为阈值，并进行皮尔逊相关系数的约束；

type2：用整体蛋白质肽链前y%作为阈值，并进行皮尔逊相关系数的约束；

type3：用单个蛋白质肽链前x%最为阈值，不进行皮尔逊相关系数的约束；

type4：用整体蛋白质肽链前y%作为阈值，不进行皮尔逊相关系数的约束.

最终我们将确定模型筛选出来的位置坐标进行线性匹配，以求找到更多的坐标点位于同一条直线.那么这些位于同一直线的坐标点所代表的序列位点，即可视为拥有强烈的序列相似性和功能相关性.

图2 不同坐标点的皮尔逊系数[14]Fig.2 Pearson coefficient of different dataset[14]

2.4 对预测结果进行归一化整合

由于预测结果各异，且有着各自的优缺点，因此我们使用数学期望对两种预测器进行数据整合，根据数学期望公式，我们可整合支持向量机打分sdv(x)与序列匹配打分Score(α,β)，具体函数如下：

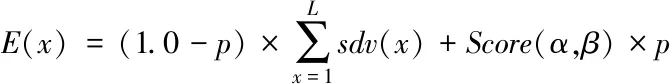
最终，对长度为L的α序列，其于β序列的结合得分为E(x).

3 结果分析

PdDNA，即本论文所研究得出的蛋白质-DNA相互作用位点位点预测方法，主要整合了SVM支持向量机打分和序列匹配度打分.在SVM模型训练过程中，我们使用PDNA_62标准实验数据集进行测试，下表为五交叉检验结果随读码窗口长度变化所得到的预测信息.我们的评估指标包括敏感度(Sensitivity，SN)、特异性(Specificity，SP)、强度(Strength)、准确度(ACC)和马太相关系数(MCC)和，其具体计算方法如下.最终确定长度11为最佳窗口长度(表1).

SN=TP/(TP+FN)

SP=TN/(TN+FP)

Strength=(SN+SP)/2

Acc=(TP+TN)/(TP+FP+TN+FN)

MCC=(TP×TN-FP×FN)/

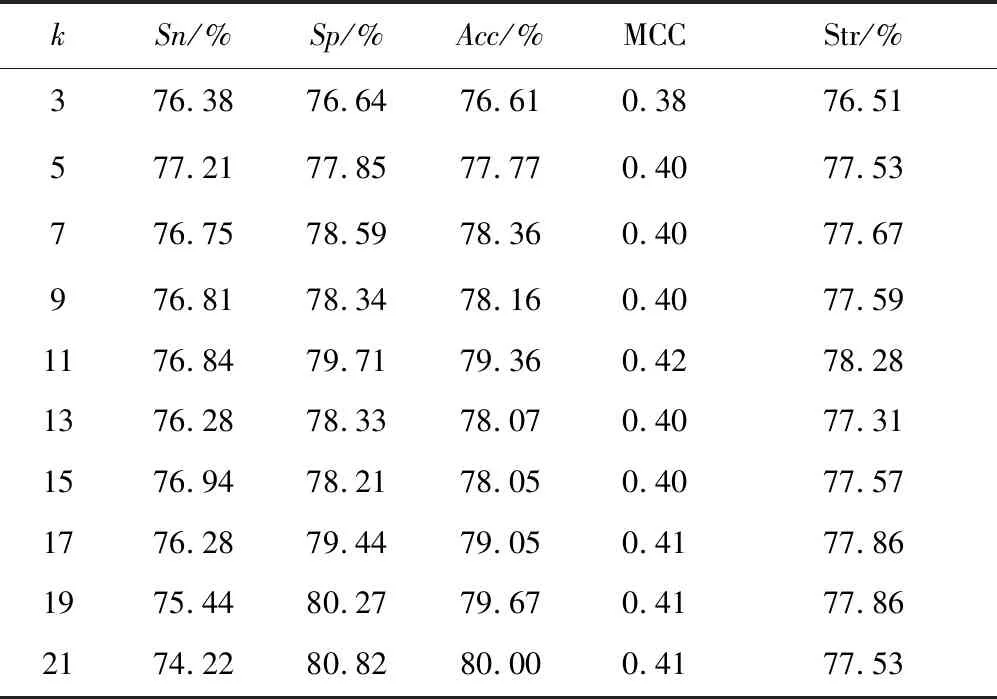
表1 PDNA_62数据集预测精度随SVM窗口长度变化情况Tab.1 The prediction result of the PDNA_62 dataset with different window sizes of the SVM

对于数据集PDNA_62，在基于PdDNA运算模型的测试中，其准确度(ACC)为85.15%，马太相关系数(MCC)0.55为，强度(Strength)为85.89%，正集预测成功率为84.91%，负集预测成功率为86.87%.与其他主流预测方法对比结果如下(表2).同时，最终预测结果的ROC曲线中(图3)也可明显看出，结合SVM与序列匹配的预测准确率比单独的SVM预测高出5%～10%不等.

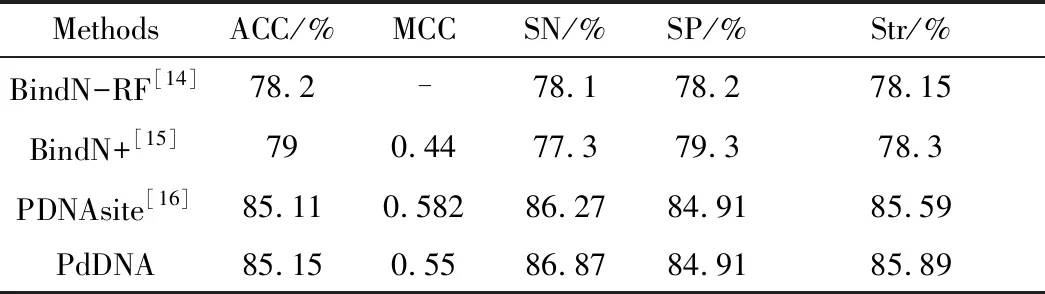
表2 对于PDNA_62数据集，PdDNA预测结果Tab.2 The prediction result of the PDNA_62 dataset of PdDNA algorithm

图3 结合SVM预测器和基于序列匹配预测器，通过ROC曲线展示数据集PDNA_62的最终的预测结果Fig.3 ROC curves for the DNA-binding sites prediction in PDNA_62 dataset by combining SVM predictor with sequence-based predictor

同时，对于自建库PDNA_224也拥有更好的预测情况(表3).从ROC曲线(图4)中可以看出，其SVM与序列匹配整合结果也比单独的SVM预测略有提高，但相比PDNA_62数据集提升幅度较小，这可能是由于我们的正负集样本数量差距进一步扩大，进而造成了SVM分类器出现偏移造成的.

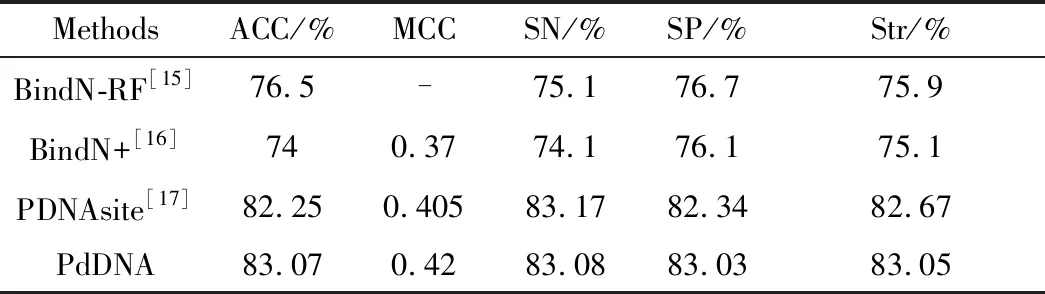
表3 对于PDNA_224数据集，PdDNA预测结果Tab.3 The prediction result of the PDNA_224 dataset of PdDNA algorithm

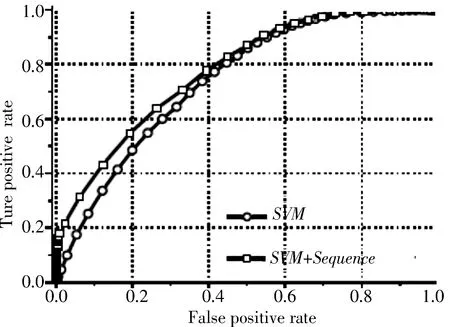
图4 结合SVM预测器和基于序列匹配预测器，通过ROC曲线展示数据集PDNA_224的最终的预测结果Fig.4 ROC curves for the DNA-binding sites prediction in PDNA_224 dataset by combining SVM predictor with sequence-based predictor

4 讨 论

在本论文中，我们通过SVM支持向量机方法、序列匹配算法的融合，得到了一种全新的用来预测蛋白质-DNA相互作用位点的实验方法—PdDNA.并根据这个方法对标准实验数据库PDNA_62进行了数据分析，结果表明我们的PdDNA程序所得到的预测结果为：ACC，85.15%；MCC，0.55；Strength，85.89%；SP，84.91%；SN：86.87%.其预测准确率高于目前蛋白质预测领域任何其他算法.其高达86%以上的预测准确度也证明了我们的预测方法具有高度的可用性和实用性，能够给蛋白质功能组学、分子生物学等其他领域的科学研究带来重要的预测参考，进一步提高科研工作的效率

同时，我们还建立了具有参考意义的PDNA_224蛋白质-DNA相互作用位点数据库.对于自建数据库的预测效果也令人满意，其最好的ACC为83.07，MCC为0.42，Str为83.05.以期对他人研究和算法设计提供有价值的数据来源.

但我们的数据集中仍存在正负样本不平衡的问题，由于客观实验限制我们很难在数据库中找到足量的正集数据.正集样本过少的情况下，其样本无法广泛分布，因此SVM预测的分类器确会朝向正集偏移，导致其敏感度下降.根据LibSVM的官方文档[18]中的说明，在特征数远小于样本数的情况下建议使用RBF内核.在RBF内核中LibSVM会启用超平面分类器，并启用了随机过抽样方法，以此对抗样本数量不平衡的问题，这也是本文中采用的解决方法.但这种方法对计算量需求极大.例如在PDNA_224数据集中，负集样本为正集样本的10倍，此时负集样本被随机抽样为10份并分别与正集样本进行建模，最终对模型进行拟合.虽精度较高但计算时间会陡增十倍.若在计算资源不足的情况下，也可以考虑手动设置惩罚因子C，对分类结果进行加权.仍以PDNA_224数据集举例，正负数据集样本比例为1∶10，则惩罚因子C比例可定位10∶1，在LibSVM中的参数则应设置为-w1 10;-w-1 1，则可在节省计算资源的情况下得到大致相同的分类结果.缺点则是会偏离原始数据的概率分布，因而本文中没有采用.