基于改进的人工神经网络对煤炭企业备件消耗预测研究 *

段军，张雪妮，宋广宇，辛立伟

(1.内蒙古科技大学 矿业研究院，内蒙古 包头 014010；2.内蒙古科技大学 信息工程学院，内蒙古 包头 014010；3.包头市联方信息自动化有限责任公司，内蒙古 包头 014010)

目前，煤矿企业对于备件的管理，总体情况是种类较多，库存结构不合理，资金大量占用等[1].为保证企业生产顺利进行，精确的备件消耗预测非常关键.

关于备件预测的大量研究，主要集中在4个方面：一是回归分析法.文献[2]提出一种机器备用零件预测方法.其不足之处是当前期样本数据较少时，预测误差较大.二是统计分析法.文献[3]用指数平滑方法预测装备维修备件的需求量.统计分析方法基于历史统计数据，并根据历史数据的变化趋势预测未来一段时间的数据.这种方法需要大样本数据构建预测模型.三是灰色预测法.此种方法适合对数据变化幅度不大的样本进行预测，否则预测效果较差.四是人工神经网络.文献[4]提出一种改进的BP神经网络预测导弹备件消耗量的方法.但人工神经网络预测模型由于过分克服学习错误而使模型的泛化能力不强，其预测效果并不是很满意.

针对以上预测方法的不足，构建一种RBF神经网络与马尔科夫链相结合的预测模型.从预测结果可以看出，该模型预测的备件消耗量准确度更高.

1 RBF神经网络和马尔科夫链

1.1 RBF神经网络结构

第一层为输入层.其作用是对数据之间的信息进行传递.作为信号源，其自身则不发生变化.

第二层为隐含层.隐含层的数量根据所要解决问题的模型而确定.隐含层在RBF神经网络结构中起到关键作用，隐含层的数量关系到预测模型的准确度.

第三层为输出层.其输出所有输入参数计算后的结果.输出层与隐含层所执行的任务不同，因此它们的学习方法也不同.其结构图如图1所示.

从神经网络结构图中可以看出，模型在训练过程中主要分为2个步骤：第一步是指在机器学习时，不需要人为的干预，自己可以监督自己来进行学习；第二步是指在系统完成建模之后，将会得到1个标准作为衡量，称之为有监督学习[5].各个参数的表达及计算方法如下：

(1)确定参数：

①确定输入向量X，X=[x1，x2，…，xn]T，n为输入层单元数.

②确定输出向量Y，Y=[y1，y2，…，ym]T，m是输出层单元数.

③确定连接权值，W=[w1，w2，…，wm]T，m是输出层单元数.

(2)计算隐含层输出值：

(1)

式中：kj是指在隐含层中第j个神经元距离中心的值，Dj为在隐含层中第j个神经元的宽度向量.‖x-kj‖2称为欧式距离.

(3)计算输出层神经元的输出：

Y=[y1,y2,…,ym]T，

(2)

y(m)=wTZ=w1Z1+w2Z2+…+wmZj.

(3)

RBF网络可以很好地处理所有非线性函数，解决一些使系统崩溃的问题，并且具有结构简单，训练速度快的优势.所以，通常数据具有非线性特点时，都会选择用RBF网络来进行仿真.RBF神经网络具有独特的优势，使得它已经应用到了生活的许多方面.

1.2 马尔科夫链

马尔科夫链是一个数列，即X1，X2，X3，…，Xn，这些序列都是随机产生的，在这个数列中可能取到的集合，称之为“一个状态的空间”.n所对应的条件概率状态是Xn+1的函数，则

P(Xn+1|Xn,Xn-1,…,X1,X0)=P(Xn+1|Xn) .

(4)

式中，X1,X2,X3,…,Xn即为马尔科夫链.

马尔科夫链是指从1个状态转移到另1个状态的过程.这个过程在模型中是随机产生的，具有无记忆性.通常情况下，在已知现在状态的情况下，并不会知道未来的状态和过去的状态，这3者是相互独立的[6].在马尔科夫链的每个步骤中，系统都会根据条件概率维持现有状态或切换到其它状态.则：

P(Xn|Xn-1,…,X1,X0)=P(Xn|Xn-1) ， (5)

比较直观的定义是：令：

A=Xn-1指过去，

B=X1指现在，

C=X0指未来，

则马尔科夫的性质为：

P(C|AB)=P(C|B) .

(6)

由上可知，马尔科夫链是对时间和区间序列均适用的典型随机过程.其仅与当前状态有关，与所有过去状态无关[7].通过现已知所有信息可以预测未来.

2 基于RBF神经网络和马尔科夫链的预测模型

2.1 构建RBF神经网络和马尔科夫链模型

神经网络在预测时，对样本数据的要求较大，样本数据决定了预测效果.但通常在预测的时候，并不能取得大量的样本数据，因此，在预测备件消耗时，为了提高备件消耗量预测的准确度，提出了使用马尔科夫链模型对其进行修改的方案，以使预测结果更接近于实际消耗量.马尔科夫链预测的目的是使动态系统随机变化.这样可以缩短预测间隔，并对于长期预测和易失随机数据序列的预测具有更好的效果.因此，建立马尔科夫链预测模型，并对RBF神经网络预测的备件消耗量进行修改，最后形成其与RBF神经网络的固定组合.它不仅可以揭示数据序列的发展和变化，而且可以提高预测模型的准确度，使预测结果更加精准.由马尔科夫链修改的RBF神经网络预测模型过程如图2所示.

2.2 马尔科夫链修正RBF神经网络预测模型

马尔科夫链作为一种预测方法，可以通过构造初始状态概率分布矩阵和状态转移概率矩阵[8]，预测出事情发生概率所处的状态.然后根据特定的系统模型校准结果，对系统进行预测，通过系统状态的变化来达到预测未来的目的.

具体的方法如下所示：

(1)马尔科夫链状态划分方法.

在用马尔科夫链建立预测模型之前，状态的划分对系统建模非常重要，会影响后期转移概率矩阵的构造.利用RBF神经网络预测出的备件消耗量和实际备件消耗量之间的相对误差，求得相对误差的均值，从而可以对相对误差的状态进行划分，并将分成S个状态.

(2)构造状态转移概率矩阵

(7)

构成转移概率矩阵时，通常情况下只考虑经过一步时的矩阵，即：

(8)

(3)计算修正后的预测值：

G(x)=m+g(x) ，

(9)

式中:m为预测的相对误差所处状态的平均值；g(x)为RBF神经网络预测的备件消耗量值.

3 模型应用

该预测方法应用于神华某煤炭公司的高频消耗备件.该公司的备件管理数据库中有2009年7月至2019年12月的数据.鉴于时间较长的数据参考价值不大，取2015年到2019年的备件出库量进行统计.经过统计可以发现，备件的出库量大部分是以3个月为1个周期进行统计，前期对备件消耗较大的高频备件展开预测，此处取其中1种备件进行预测.表1是某备件2015年到2019年的出库量统计.

表1 某备件出库量统计表

3.1 基于RBF神经网络的备件消耗预测

结合RBF神经网络预测模型，通过Matlab编程，将样本数据分为训练数据和测试数据，进而确定神经网络层和节点数目的大致范围.利用2015年3月到2018年12月的数据进行训练和测试.运用滚动预测的方法将2015年3月到2016年3月n条数据作为网络的输入，2016年6月k条数据为网络的输出；以此类推组成训练样本.其中n=5,k=1.

在训练RBF神经网络预测模型时，首先，对备件出库量的样本数据进行归一化处理.然后对归一化后的数据进行训练，即可得到预测备件消耗量值，同时经过计算可以得出相对误差值.将RBF神经网络训练得到的样本备件消耗量的相对误差分为4个状态S1=(-5.2，-2.52]，S2=(-2.52，0.16]，S3=(0.16，2.84]，S4=(2.84，5.52].具体划分状态见表2.

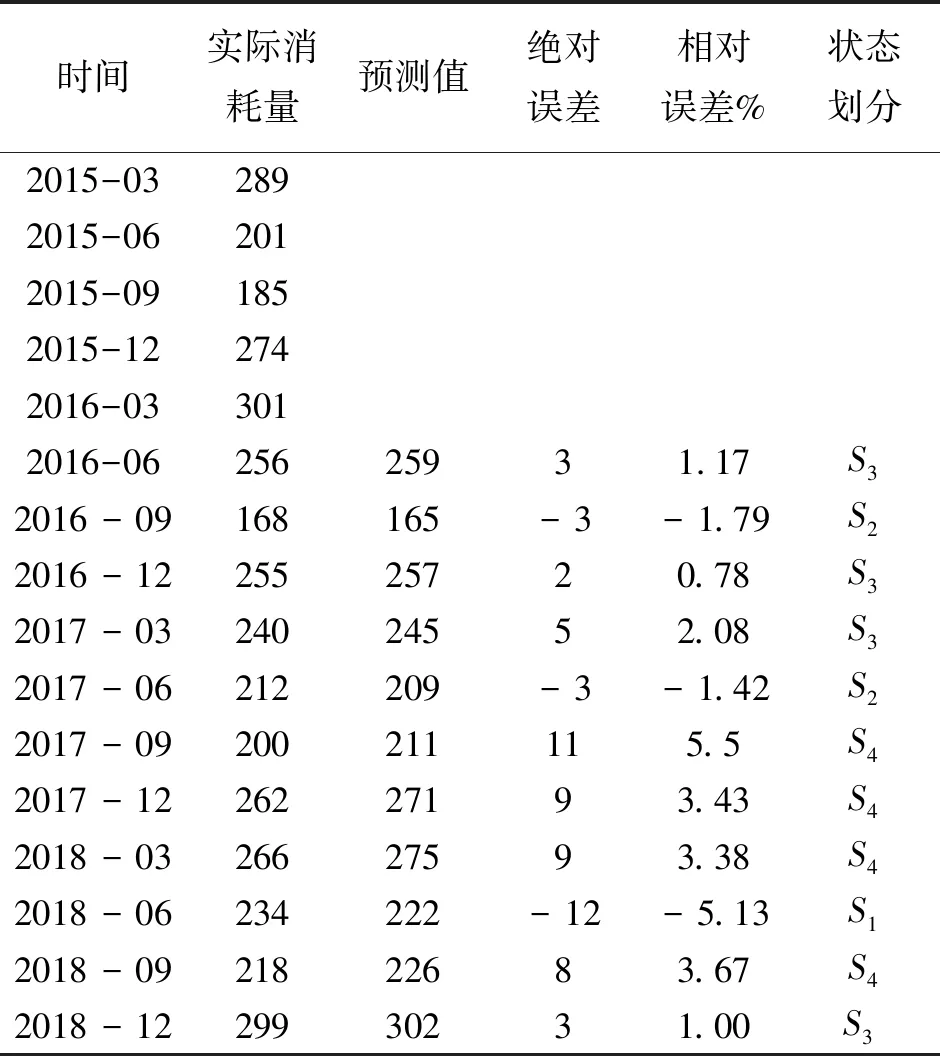
表2 RBF神经网络预测值表

3.2 修正误差马尔科夫链的残值

由表2可知，RBF神经网络预测的备件消耗量有较大误差，因此，为了使预测值更加准确，引入马尔科夫链来修正预测值.

根据表2可以得到，在某一时刻该序列所处状态集的具体划分，然后，根据式(7)和(8)计算得到转移概率矩阵.通常情况下，计算时只需考虑一步状态的转换矩阵，转换矩阵如下：

由式(9)可以得出修正后的预测结果，并应用此方法可以预测2019年3月到2019年12月的备件消耗量.其结果如表3所示，包括测试集数据以及预测验证集数据.备件消耗量预测结果的对比图如图3所示.

从修正结果可以看出马尔科夫链修正的RBF神经网络模型提高了备件消耗量预测的准确度，使修正值更加接近于实测值.

表3 对比RBF神经网络和马尔科夫链修正值结果表

4 结论

结合煤炭企业高频消耗性备件的需求预测问题，首先用RBF神经网络预测神华某煤炭公司的备件消耗量，预测显示RBF神经网络的预测值误差较大.为了提高预测的准确度，然后对RBF神经网络的预测值进行优化，选择用马尔科夫链修正误差残值的方法，构建了一种RBF神经网络与马尔科夫链相结合的预测模型.从对比上述示例的预测结果可以看出，与传统的RBF神经网络预测方法相比，基于改进的RBF神经网络预测模型的预测值更加接近于实际的备件消耗量值.同时将该模型引入神华某煤炭公司高频消耗备件预测中，并将该方法应用到该公司的备件管理系统中.结果表明，该预测模型预测准确度高，而且在系统预测时，速度较快，对神华某煤炭公司来说，具有一定的应用价值.