由一道学生错题引发的思索

张慧清

（重庆市武隆区实验中学 重庆武隆 408500）

对于凹多边形和凸多边形，在人教版的初中教材八年级上册第20页中写道：“本节只讨论凸多边形”，在相对应的教学参考书中，第23页也写道：“多边形分凹凸两类。因为我们现在只研究凸多边形，所以教科书只定义了凸多边形，要求学生能根据定义辨认一个多边形是不是凸多边形就可以了。教科书没给出凹多边形的概念，教学中也不必对学生讲。”因此从教十几年来，我从来都没有去想过研究凹多边形，更别提拓展给学生了。但最近的一道数学试卷上的题却让我反思：我们在教学中是否应该拓展学生，让学生能获得更多的思考方法，让学有余力的学生多一些方法去解题。

虽然教材中没有，但在各种练习册只都出现了有关凹四边形或者凹多边形的题目，以前我们都是化为凸多边形来解决，但如果能多探讨一些关于凹多边形的知识，学生会获得更多的解题思路：

题目是这样的：

25.如图1：BE平分∠ABD，CF平分∠ACD，且BE与CF相交于点G.

若∠BDC=1400，∠BGC=1050，求∠A的度数。

猜想：∠A与∠BDC，∠BGC的关系，并证明。

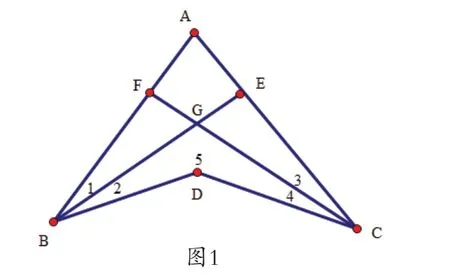
我班的张铃同学对第（2）个问题的证明方法是这样的:证明：∠BDC+∠BGC=1800-1/2∠A，证明如下：

∵∠5=3600-∠BDC

∴在四边形BGCD中，∠2+∠4=3600-∠5-∠BGC=3600-（3600-∠BDC）-∠BGC=∠BDC-∠BGC

∵BE平分∠ABD，CF平分∠ACD

∴∠1=∠2，∠3=∠4

∴∠1+∠3=∠2+∠4=∠BDC-∠BGC

在四边形ABDC中，∠A=3600-（∠2+∠4）-（∠1+∠3）=3600-2（∠BDC+∠BGC）

∴∠BDC+∠BGC=1800-1/2∠A

首先看到他做的题时，我意识到他是在用凹四边形的知识来做，但他的结论与参考答案中的不一样，因此我并不确定他的答案是否正确。我在他的试卷上做了批注：“本章我们学的是凸多边形，不是凹多边形。”我告诉他，我要去找找资料，看凹四边形是否也有和凸四边形同样的结论，因此开始了我对这道题目的探索之旅。

第一步，我在网上查找资料，想证实凹四边形的内角和是否也为3600。结果发现，因为无论凹凸，都能分成两个三角形，因为三角形的内角和为1800，所以无论凹凸，四边形的内角和都为3600。

第二步，我同时在网上还搜索到图2这种形状的凹四边形有一个非常重要的性质：∠BDC=∠A+∠B+∠C，可以用以下的几种方式来证明：

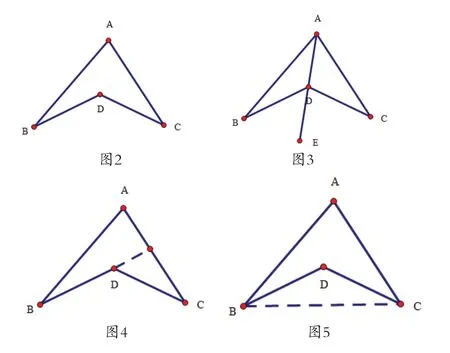
而且应用非常广泛，在本章试卷中就有关于这个题目的证明题。

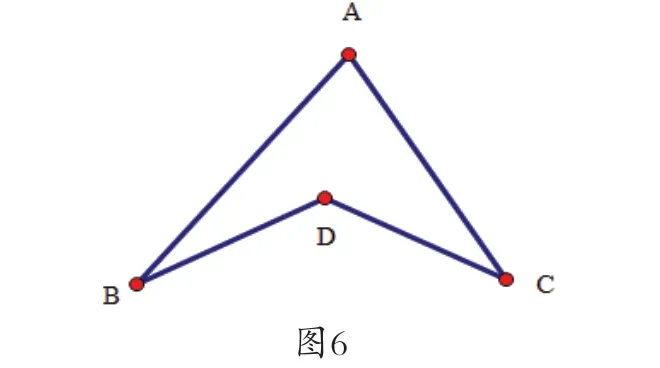
23.（1）如图6，求证：∠BDC=∠A+∠B+∠C。

（2）如果点A与点D线段BC的两侧，猜想∠BDC， ∠A， ∠ABD， ∠ACD这四个角之间的关系，并证明。

第三步，那他的这个解答过程到底错在哪里呢？经过我的仔细查找，发现问题出在两个方面。首先是在运用“∠BDC-∠BGC”的过程中，把“-”号写成了“+”号；然后是他在计算∠A的过程中没有减去∠BDC的外角，也就是∠5。我再将它代入进去：∠A=3600-∠ABD-∠ACD-∠5=3600-2(∠BDC-∠BGC)-(3600-∠BDC)=2∠BGC-∠BDC ，所以2∠BGC=∠A+∠BDC。也就得到了本题的正确答案。或者这个题也可以用上面的性质来证明：

∵∠BDC=∠A+∠ABD+∠ACD=∠A+∠1+∠2+∠3+∠4，

∠BGC=∠A+∠1+∠3

∴∠BDC=∠A+2(∠BGC-∠A)=2∠BGC-∠A

∴2∠BDC=∠A+∠BDC

做完这个题目，给了我许多思考，在我们教书的过程中到底应该如何去教。对于学生做的题，首先应该去认真的体会，不能光看结果的对错，要帮助学生认识到错在了哪个地方。其次，要用教材，还要走出教材，教材不教，不意味着学生的思维不去想，对于学有余力的学生，要引导学生用多种思路去思考，这就对老师的教学能力提出了更高的要求。必须要提高自己的专业知识，才能用更广阔的思路去解决问题。

后来，我把这道题的错误之处讲给了这位同学，表扬了他，并且把他的思路在班上讲了。现在，我会在教学的过程中把教学参考书中的一些合适的拓展资源和教材章后的阅读与思考拓展给学生，希望学生能看的更远，走的更远。