基于混沌粒子群算法的赛车避障问题研究

徐 棚 张乾元 王好问

（重庆邮电大学通信与信息工程学院 重庆 400065）

引言

赛车游戏已经产生多时，因为赛车游戏高速的赛车操作体验、丰富的奖励机制、高速刺激感、挑战性，在游戏玩家中有着广泛的吸引力。大多数赛车游戏中，主要通过速度加减以及道具拾取等起到增加游戏乐趣的效果。

游戏玩家对于赛车游戏有丰富的见解，对于如何躲避障碍物、尽可能提高速度就是赛车游戏的关键之处。本文对于赛车避障问题进行分析给出其解决方案。

一、工程需求

赛车游戏中地面上有障碍球和能量球。两种球都静止不动，被撞后会消失。撞上障碍球赛车的速度会降低20%，撞上能量球赛车的速度会提高10%。电脑屏幕的分辨率为1000×800。

要求：用户看见能量球或障碍球的反应为0.2秒，最快按键每秒8次。当障碍球已经完全出现在屏幕正前方，赛车以速度v向上运行，v最小多少时，用户不可能躲开该球。

二、方案设计与实现

根据直观分析，临界值可能存在的点有6个，满足此6个边界条件即可保证赛车一定不会碰到该球。由于躲避时赛车和球处于同一竖直线上，根据对称性，为统一计算，设看到该球后均选择向右闪躲。故此6个临界点与该球的位置排布方式如下：

按从下往上的顺序命名以上6个点，故可知对应每个点的竖直向距离y(i)可表示为：

其中H=800p表示屏幕的纵向长度大小，h*=10p表示赛车的边长。已知h0=20p， h1=19p， h2=18p，h3=17p，h4=15p，h5=13p

设第j次与第j+1次按减速键之间的时间间隔为 ，竖向位移的表达式满足下式：

同理竖直方向的速度条件，水平向的距离也与6种情况相关。具体表示为：

设第k次与第k+1次按减速键之间的时间间隔为Δtk，竖向位移的表达式满足以下公式：

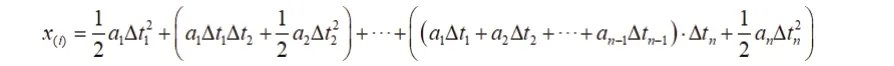
设在最优按键操作的条件下能够恰好躲避障碍球/能量球的速度为v，故最终目标即可表示为：

求解模型需要确定最优按键次数以及任意时间结点处的具体按键操作，按键次数较多，属于高维问题，为此我们采用混沌粒子群算法求解[1]。

2s内有长度16的按键序列，按键序列每两个元素间隔0.125s，对序列元素有以下设置：

对每组序列计算出每个序列，使刚好能躲避速度的最大值作为每个粒子的适应度。

速度v最小为1018.96p/s时，用户不可能躲开该球。

三、结束语

本文针对赛车游戏中避障问题，进行建模分析并使用混沌粒子群算法给出了避开/撞上障碍物的临界条件。