时间尺度上约束Hamilton 系统的Lie 对称性
陈志炜, 朱建青
(苏州科技大学 数理学院,江苏 苏州215009)
用奇异Lagrange 函数描述的系统,称为奇异系统。 在物理学中,奇异系统广泛存在。 例如自然界的四种基本作用力、 引力场、 杨-Mills 场、 超对称理论。 奇异系统通过Legendre 变换, 由Lagrange 描述过渡到Hamilton 描述时,会产生一个固有约束,由此称之为约束Hamilton 系统[1],又称奇异系统Hamilton 正则方程。
对称性理论对于研究力学、数学、物理学等基础学科起着非常关键的作用。 由对称性可以导出系统的守恒量,主要方法有:Noether 对称性、Lie 对称性、Mei 对称性等。 用对称性理论来研究约束Hamilton 系统的守恒量已经取得了很多成果。李子平[2]在1991年提出了奇异系统在位形空间与相空间中的Noether 定理。王永龙和赵德玉[3]将Noether 对称性及正则量子化推广到了约束Hamilton 系统中。 张毅和薛纭[4]在考虑系统仅含第二类约束的情况下,根据Lie 对称性理论得到了约束Hamilton 系统的守恒量。
时间尺度理论由德国学者Hilger[5]于1988年首次提出,运用时间尺度理论不仅能够把连续和离散系统统一起来,而且能将动力学系统的物理本质刻画得更加清晰准确。 随着时间尺度基本理论的不断完善,在时间尺度理论的基础上研究动力学系统的对称性与守恒量逐渐成为了一个热门的研究方向,至今已经取得了很多重要的成果[6-16]。 笔者将在时间尺度上研究约束Hamilton 系统的Lie 对称性与守恒量问题。
1 时间尺度上约束Hamilton 的正则方程
假设力学系统的位形由n 个广义坐标qs(s=1,2,…,n)确定,时间尺度上系统的Lagrange 函数为L=L(t,qσ,qΔ)。 设则通过Legendre 变换,由Lagrange 描述过渡到Hamilton 描述时,存在如下约束

引进时间尺度上的广义动量和正则Hamilton 函数

对(3)式进行等时变分

将(2)式代入到(4)式,有

将方程(5)等式两边对ps求偏导,得


将(6)式和(7)式代入到(5)式中,得

利用Euler-Lagrange 方程,有

合并(5)式和(8)式,再将(9)式代入,可得

约束条件(1)式满足虚位移和等时变分的限制条件为

引进Lagrange 乘子λj,由(10)式和(11)式,可得系统正则形式的运动微分方程为
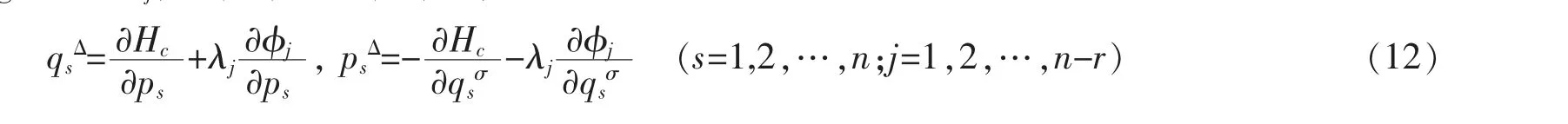
由泊松括号,可将(12)式写成

其中HT=Hc+λjφj称为总Hamilton 函数。
在运动微分方程积分之前,可由(1)、(12)式求出λj(t,qσ,p),则方程可以进一步写为

其中
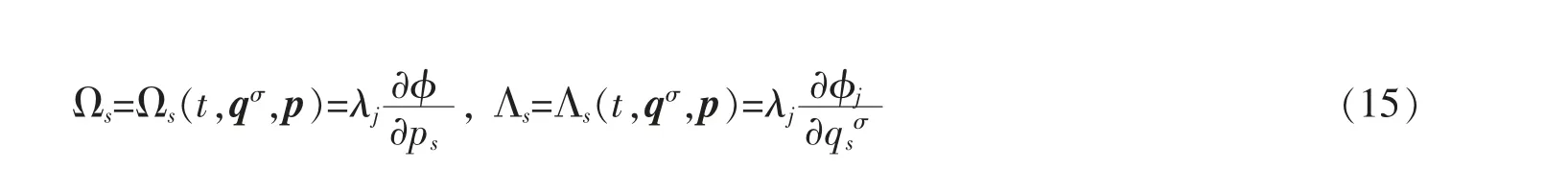
考虑约束(1)式为第二类约束[1],有

那么(12)式中所有的Lagrange 乘子λj可完全确定[1],有λj=λj(t,qσ,p)。
2 时间尺度上的确定方程、限制方程和附加限制方程
取时间t 和广义坐标的无限小变换

其中,ε 为无限小参数,ξ0、ξs、ηs为生成元。
无限小生成元向量和它的一次扩展为[12]

根据Lie 对称性理论,微分方程在无限小变换下和原方程是保形不变的,方程(14)在变换(17)下的不变性可表示为

称(20)式为系统的确定方程。
约束(1)式在变换(17)下的不变性可表示为如下限制方程

定义1如果ξ0、ξs、ηs满足确定方程(20),则称该对称性为相应自由Hamilton 系统的Lie 对称性。
何家弘在其论著中描述“证据保全是指用一定形式将证据固定下来,加以妥善保管,以便司法人员或律师分析、认定案件事实时使用”。[2]根据电子数据保全自身特点,结合传统的证据保全概念加以分析。可以表述为,电子数据保全是指那些以后难以提取的或者容易损毁的电子数据,由人民法院,公证处和其他保全机构、组织依照职权和当事人的主动申请,对电子数据进行固定和采取一些保护措施。它其实是为了保全电子数据的完整性和客观性,用符合规定的手段和方法进行固定,为相关诉讼活动提供证据支持。
定义2如果ξ0、ξs、ηs满足确定方程(20)和限制方程(21),则称该对称性为时间尺度上约束Hamilton 系统的弱Lie 对称性。
由微分方程的导出过程,存在如下的限制

将等时变分代入(22)式,有
称方程(23)为附加限制方程。
定义3如果ξ0、ξs、ηs满足确定方程(20)、限制方程(21)和附加限制方程(23),则称该对称性为时间尺度上约束Hamilton 系统强Lie 对称性。
3 时间尺度上的结构方程与守恒量
定理1在ξ0、ξs、ηs满足确定方程(20)的条件下,若存在一个规范函数G=G(t,qσ,p)满足结构方程则时间尺度上相应自由Hamilton 系统存在守恒量

证明

定理2对于满足确定方程(20)和限制方程(21)的ξ0、ξs、ηs,如果能够找到一个规范函数G=G(t,qσ,p)满足结构方程(24),则系统存在形如(25)式的弱Lie 对称性守恒量。

则系统存在形如(25)式的强Lie 对称性守恒量。
定理4如果T=R,σ(t)=t,μ(t)=0,守恒量(25)式成为经典的仅含第二类约束的约束Hamilton 系统的Lie 对称性守恒量[4]

4 算例
定义时间尺度T={2n:n∈Z}∪{0},假设系统的Lagrange 函数为

研究系统Lie 对称性与守恒量问题。
系统的广义动量为

正则变换之间存在两个固有约束

系统的正则Hamilton 函数为

总Hamilton 函数为

由约束的相容性条件[1],得

系统的运动微分方程为

由确定方程(20),得

由限制方程(21),得

由附加限制方程(23),得

由(35)、(36)、(37)式,可得一组解为

将(38)式代入结构方程(26),可得规范函数为

由(39)式,可得

由(25)式,系统对应的守恒量为

下面验证算例中守恒量的正确性

5 结语
通过引入时间尺度上的正则Hamilton 函数和广义动量, 用Lie 对称性的方法研究了时间尺度上约束Hamilton 系统的守恒量。 给出强Lie 对称性和弱Lie 对称性的定义,最终得到了时间尺度上守恒量的具体形式和存在条件。 根据文中的研究方法,可以进一步把Mei 对称性和联合对称性的理论拓展到时间尺度上的约束Hamilton 系统中,从而进一步丰富约束Hamilton 系统的研究。

