基于滑模观测器的风电机组超扭曲MPPT 控制

曹松青， 郝万君， 陈歆婧， 王 飞， 王 昊， 孙志辉

（1.苏州科技大学 电子与信息工程学院，江苏 苏州215009；2.吉林欧科自动化设备有限公司，吉林省 吉林市132021）

风电系统是一个非线性时变系统，系统参数随着运行工况的改变有较大的变化[1－2]。 为了提高风能利用效率，需要引入较为先进的控制算法[3]。

在最大功率跟踪方面，国内外已经有大量的研究，可以分为两类：第一类是最优曲线法；第二类是寻优法，也叫爬山法、黑箱法[4]。 第一类算法中典型的代表有：最佳叶尖速比法[5-6]、功率信号反馈法[7]、最佳转矩法[8-9]。 第二类算法中典型的代表有：定步长爬山法[10]和变步长爬山法[11-12]。 文献[13]提出基于滑模控制的最大功率跟踪方法，具有较好的鲁棒性和控制精度，但此方法依赖于风速数据的精确测量，这在实际中很难做到。文献[14]采用二阶滑模控制器调节发电机转子电压，跟踪最优转速和转子电流，动态响应迅速，跟踪效果好，但未考虑系统中存在的不可测状态。 文献[15]采用高阶滑模算法控制双馈感应风力发电机，输出抖振较小且鲁棒性高，但算法过于复杂，实现难度大。

超扭曲算法是非线性滑模控制策略中的一种，对各种外部干扰以及模型的不确定性具有较好的鲁棒性能，能实现准确的调节和跟踪。与常规滑模控制策略相比，所施加的控制动作是连续的，有利于抑制抖振。其相对简单的控制律，有利于减轻实时计算的负担[16]。

文中首先运用机理分析方法对风力发电机组进行建模。 为了得到有效风速，采用最小二乘支持向量机（LS-SVM）算法进行风速估计。 提出了一种基于最佳转速的超扭曲控制策略，并设计滑模观测器对不可测的系统状态进行观测，以更好地实现风力发电机组的最大功率跟踪，同时减小发电机转矩抖振、缓解机械疲劳。最后利用Matlab／Simulink 软件进行仿真分析。

1 风力发电机组模型

风力发电机组的运行状态可以分为三个阶段：（1）启动阶段，风速从零上升到切入风速；（2）低风速阶段，风速介于切入风速与额定风速之间；（3）高风速运行阶段，风速介于额定风速与切出风速之间[16]。笔者的研究重点是在切入风速和额定风速之间的低风速区域，为了充分捕捉风能，常将桨距角设为0°。 风力发电机组从风能中转换的真实功率可表示为

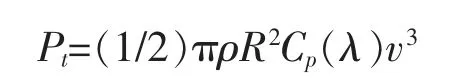
其中，v 为风速，ρ 为空气密度，R 为风轮半径，Cp（λ）为风能利用系数。当桨距角一定时，Cp（λ）是一个关于λ 的非线性函数，叶尖速比λ=RΩ/v，其中Ω 为风轮转速。 风力发电机的输出功率为Pe=ηPt，其中η 为发电机效率，通常为0.83。

图1 风能利用系数与叶尖速比关系图

图1 为风能利用系数与叶尖速比的关系图，如图所示，当叶尖速比达到最佳时，风能利用系数最大。 叶尖速比的调节可以通过控制风轮的转速跟踪其最佳参考值来实现，即

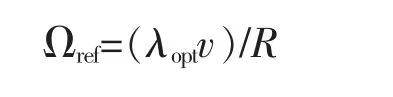
由Pt=TtΩ 可得风轮的气动转矩为

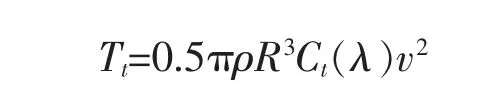
其中，Ct（λ）=Cp（λ）/λ。

然后，通过应用牛顿第二定律，设摩擦、不确定性和其他干扰的项为g（·），可以直接获得系统的非线性动力学方程，即

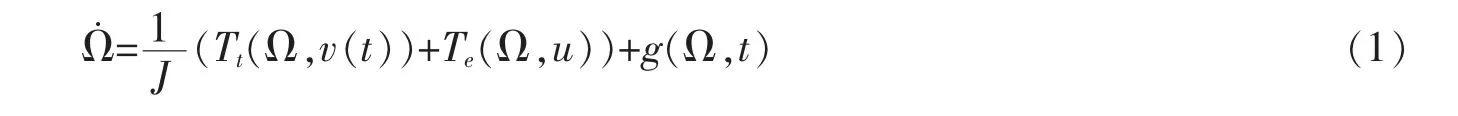
其中，J 为转动惯量，Te为发电机电磁扭矩，u=|cosα|通过受控制的触发角α 对发电机转矩进行控制。

其中发电机电磁转矩可表示为

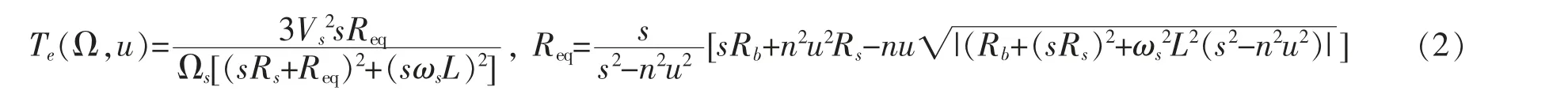
其中，Rb=Rr+0.55Rf，L=Ls+Lr；Rs、Rr、Rf分别为定子、 转子和直流环电阻；Ls、Lr是定子和转子绕组的漏电感；Ωs和ωs分别为机械和电气的同步转速；V 为定子电压；n=n1/n2，n1和n2分别是发电机和降压变压器的匝数比。

图2 为风力发电机转矩和转速关系图， 实线表示随控制变量u 变化的Te和Ω 的变化曲线， 对于不同的风速，Tt的变化以细虚线表示，最佳叶尖速比的轨迹以粗虚线表示。

图2 风力发电机转矩和转速关系图

2 控制器设计

2.1 风速估计

由于风力机处于三维时变的风场环境中，风速在整个风轮旋转平面上分布不同，风速计很难准确测量有效风速。又由于风速的变化会直接影响Ω 和Tt的变化，因此，可以依据三者关系，由易测的Ω 和Tt对有效风速进行估计[17]。 文中通过最小二乘支持向量机（LS-SVM）建立风速估计模型来得到有效风速的估计值，风速估计模型可表示为

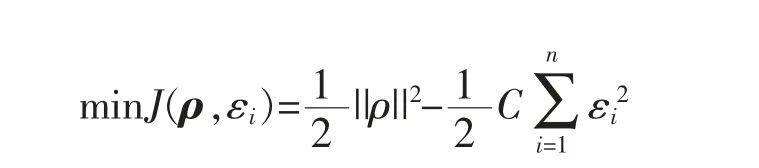
式中，C 为惩罚因子；ρ 是权向量；εi为误差变量。 约束条件

根据拉格朗日函数可以求得风速估计模型为

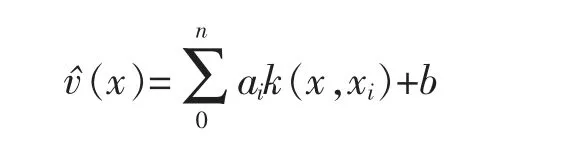
其中，ai为拉格朗日乘子；b 为阈值；k（x，xi）为核函数，其表达式为

2.2 超扭曲滑模控制器设计

为简单起见，式（2）的发电机电磁转矩可以表示为

其中，ΔTe（Ω，t）为存在的转矩误差，式中前两项的和对应发电机转矩的近似表达，如图2 中点画线所示。当转矩低于额定值时，如图2 所示，ΔTe（Ω，t）相当小，式（3）中前两项的和更加接近发电机电磁转矩的真实值。

将式（3）代入式（1）得

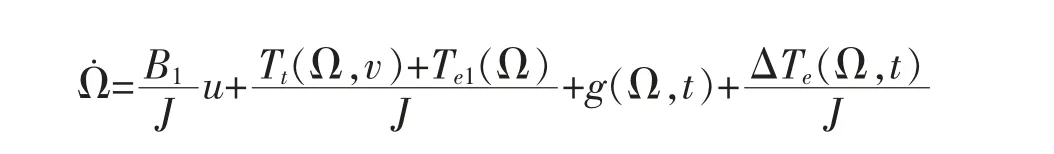
为了实现最佳转速跟踪，选择滑模变量为

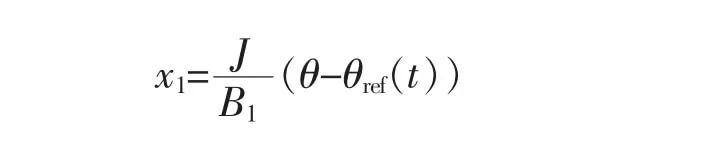
令x2为

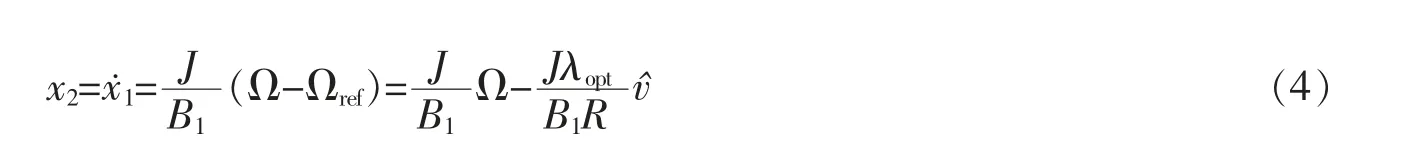
当滑模变量满足x1=0，x˙1=0，可实现控制目标Ω=Ωref，即风轮转速跟踪最佳转速。 对式（4）求导得

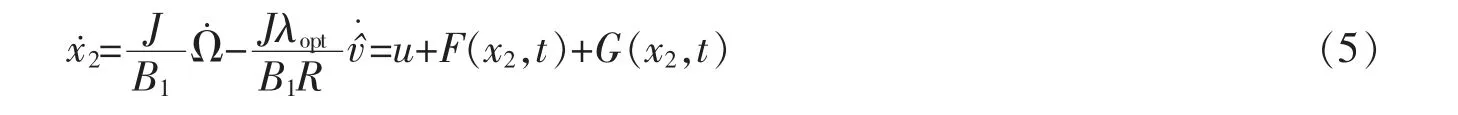
将上式代入式（5）得

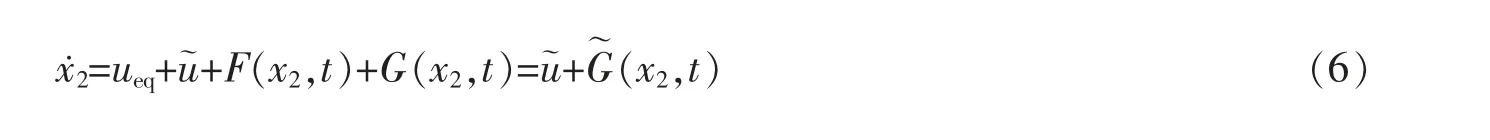
设置滑模面为：s=c1x1+x2。

取滑模面的导数

其中c1＞0，将式（6）代入得

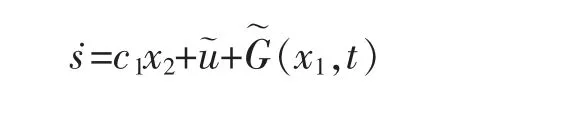
设置控制变量为

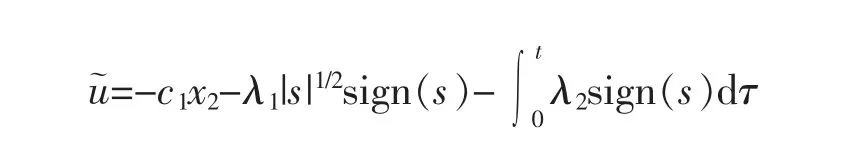
式（8）也可以表示为

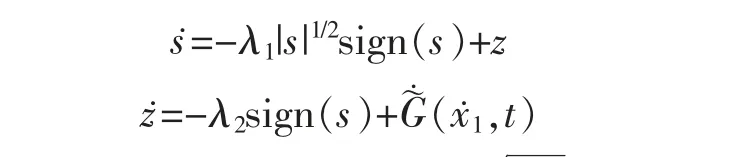
因为上述控制器是在某个固定采样时间实现的，因此，在采样间隔内，不连续项k2sign（e1）的值将是恒定的，所以该方法可以实现连续控制。

2.3 滑模观测器

其中，z1、z2为修正项设则动态误差可表示为

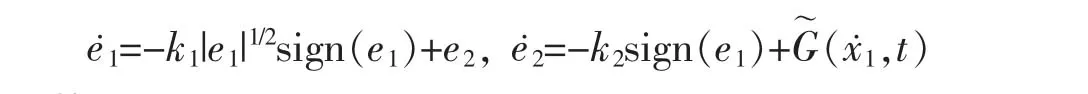
对上式求导得

综上所述，带观测器的滑模控制器可以表示为

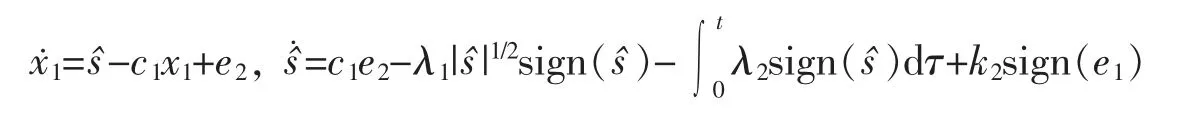
上述最大功率跟踪控制系统结构如图3 所示。

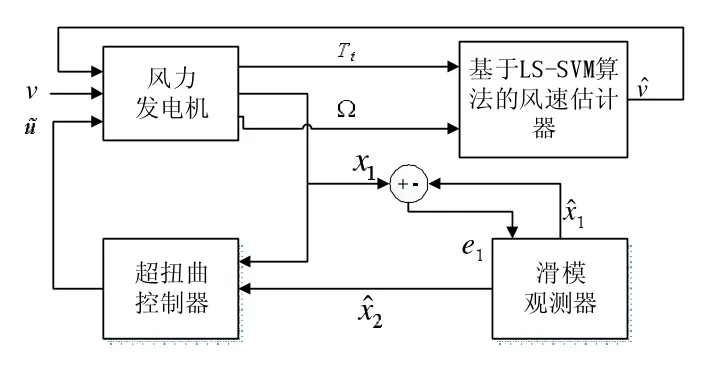
图3 基于超扭曲滑模观测器的风机最大功率跟踪控制系统结构图

3 仿真与分析

依据上述分析，应用Matlab/Simulink 对基于滑模观测器的超扭曲控制器（STO-STC）性能进行仿真验证。 为了进行控制效果对比分析，引入了最佳转矩控制法（OT）和常规滑模控制（SMC）。

风机参数：转动惯量J＝534.116 kg·m2，风机叶片长度R=64.5 m，空气密度ρ=1.225 kg·m2，Vs=460Lf=10.1 mH；设置控制器参数λ1=153.5944，λ2=11533.5，滑模观测器参数k1=15，k2=110。

图4 估计风速曲线

图4为通过LS-SVM 风速估计器得到的估计风速（v_estimate）曲线与实际风速（v_real）曲线的对比图，其中实际风速采用美国国家能源部可再生能源实验室开发的TurbSim 软件生成，平均风速为8 m·s-1。 基于上述LS-SVM 风速估计原理，对采样值进行标准化变换后再仿真。 利用400 个样本点验证已用2000 个数据训练好的支持向量机模型。 可见，估计风速与实际风速相比具有一定的滞后性，但估计精度较高，均方差只有0.0875。

图5 为在连续自然风速模拟条件下， 基于滑模观测器的超扭曲控制器 （STO-STC）、 最佳转矩控制器（OT）和常规滑模控制（SMC）在实现最大功率跟踪过程中的转速跟踪曲线、风能利用系数Cp变化曲线、发电机输出功率曲线以及发电机电磁转矩曲线。

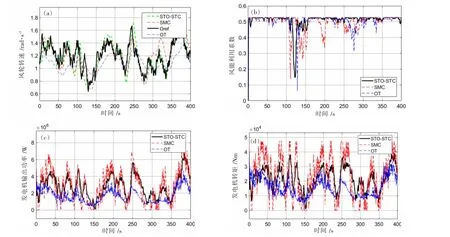
图5 最大功率跟踪响应曲线图

由图5（a）可见，三种控制策略都可以一定程度地跟踪最佳转速（Ωref），但STO-STC 的跟踪性能明显优于OT 和SMC。 由图5（b）可见，相较于OT 和SMC，STO-STC 可以使风能利用系数Cp波动更小、更好地稳定在最佳风能利用系数0.52 附近，从而提高了风力机捕捉风能的能力，但不可否认的是，在100～150 s 风速大幅度下降的时段，风能利用系数也明显下降，这是由于风电机组是一个具有大惯性的系统，使得风能蕴藏在巨大的转动惯量中。 由图5（c）可见，采用OT 时发电机输出功率较另两种方法偏小，这是由于其风能利用系数最低的缘故，同时，采用SMC 时输出功率波动最为明显，这不利于后续的并网运行，从而影响发电质量。分析图5（d）可知，相对于SMC 而言，STO-STC 转矩的波动较小，抖振现象得以抑制，有利于缓解风机机械疲劳，延长其使用寿命。 综上所述，STO-STC 不仅能提高风能转换效率，而且能有效抑制常规滑模控制具有的抖振现象，整体效果最好。

4 结语

笔者提出了一种基于滑模观测器的风力发电机组最大功率跟踪的超扭曲滑模控制器，并利用风速估计器和滑模观测器对风速以及风机系统中不易测量的状态进行估计。 仿真实验证明，在随机风速下，该方法具有较好的最佳转速跟踪性能，且能有效抑制发电机转矩的抖振，具有一定的工程应用价值。