经历探究过程 获得数学结论

黄红

【摘 要】 数学是一门需要理论结合实践的课程。教师在进行理论知识教学的过程中，需要同时指导学生进行实践探究，在实践中引发猜想、实验验证以及获得结论。

【关键词】 初中数学;实践探究;数学验证

一、经历操作过程，引入探究内容

在“多边形的内角和”一课的教学中，首先我引导学生借助一张长方形纸开展操作活动。

师：同学们，你们现在手中都有一张长方形纸片。现在需要把这张长方形纸片任意地剪掉一个角，你能想到几种剪法？剪掉之后变成了什么形状？大家先自己操作一下，再和同学们交流自己的方法。

（学生经过思考进行操作，然后全班交流）

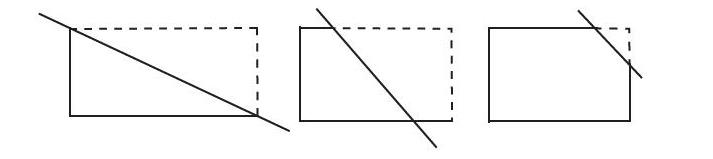
生1：把长方形的一个角剪掉，剩下的图形可能是三角形，也可能是梯形。

生2：把长方形的一个角剪掉，除了他说的三角形和梯形，还可以得到五边形。

师：你们能到黑板上把剪的过程画一画吗？（学生上台画）

师：把长方形的一个角剪掉后会变成三角形、梯形或五边形。这些图形都属于“多边形”，这一节课我们来研究“多边形的内角和与外角和”。

研究“多边形的内角和”的基础是“三角形的内角和”，以上片段中让学生借助操作活动，不仅能够引入课题，而且能够在这个过程中初步感受到“多边形的内角和”与“三角形的内角和”的联系，从而为接下来的数学探究奠定基础。

二、经历探究过程，获得数学结论

在初中数学课堂教学中，引导学生经历数学探究的过程是十分重要的，学生在数学探究过程中获得的数学结论才是他们自己的。因此，在引入课题以后，我从以下几个环节引导学生进行数学探究。

1.引导数学猜想，感知数学结论

师：同学们，你们觉得一个四边形的内角和会是多少度？

生1：我觉得四边形的内角和是360°。

师：为什么呢？能说说原因吗？

生2：因为正方形和长方形的每个内角都等于90°，所以四个角加起来就是360°。

生3：我觉得你的说法不对，你说的正方形和长方形属于特殊四边形，不具有普遍性，不能证明任意四边形的内角和都为360°。

师：你的思维真严谨。在小学的时候，我们对长方形和正方形都已经有了一定的认识，知道它们的内角和为360°，因此我们猜想任意四边形的内角和也一样。那么这个猜想到底对不对呢？这需要我们用理论知识来证明。

在这个环节中，唤醒学生小学时学过的关于长方形和正方形的内角為90°的知识，学生对任意四边形的内角和进行了猜测。这种方式有利于学生体会从具体到抽象、从特殊到一般的数学思维方法。

2.引导数学探究，获得数学结论

师：对于比较复杂的问题，我们一般都是用化未知为已知的方法，利用已经掌握的知识对新的问题进行研究。你们觉得可以把四边形的内角和转化成什么来研究？

生：可以转化成三角形来证明。

师：是的，大家都很聪明！都想到了用三角形的有关知识来解决四边形的问题。

师：那么如何进行转化呢？

生：可以画辅助线。

师：那请大家想一想具体的验证方法吧。

学生在草稿本上画图验证，教师巡视。学生用了三种把四边形分成几个三角形的方法，如下所示：

师：下面请同学们上来用实物投影仪展示自己的方法，同时讲一讲自己是怎么想的。

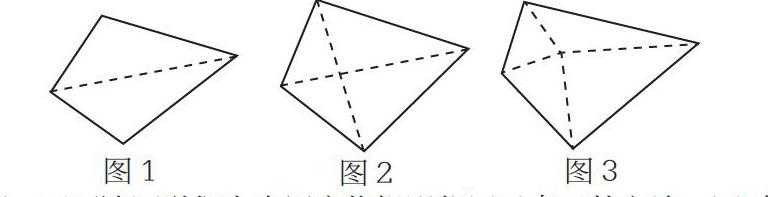
生1：如图1所示，我用一条辅助线把四边形分成了两个三角形，因为三角形的内角和为180°，所以四边形的内角和就等于360°。

生2：如图2所示，我把四边形分为四个三角形，然后就可以用四个三角形的内角和减掉中间的一个圆周角度数，最终的结果等于360°。

师：还有不同的方法吗？

生3：其实可以在这个四边形内随意取一个点，然后和四个顶点相连，这样就得到四个三角形，如图所示，用四个三角形的内角和减掉中间的一个圆周角度数得到360°。

师：你们觉得这三种方法哪一种更具有普遍性？

生：第三种方法更具有普遍性。

在这个环节中，学生根据自己的理解通过画一画对四边形的内角和进行了探究，在这个过程中体验到了把四边形分为几个三角形来解决问题的优势。

三、引导类比迁移，拓展数学结论

师：同学们，你们经过自主探究证明了“四边形的内角和为360°”这一结论。那对于五边形、六边形、七边形等，它们的内角和分别是多少呢？请大家在小组内四人合作探究，然后推论出n边形的内角和度数。

学生在四人小组内借助研究四边形内角和的方法对五边形、六边形、七边形的内角和进行了探究。在这个过程中，他们发现五边形可以划分为五个三角形、六边形可以划分为六个三角形、七边形可以划分为七个三角形……并根据三角形的内角和等于180°推导出了n边形的内角和规律。

师：你们真厉害！在历史上，这一规律人们花了很长的时间才发现，而大家在这一节课的时间里就发现了。不过在数学中为了清晰地表达规律，一般都会用简洁的字母公式来表示，同学们动动脑，试试能否用一个公式把多边形的内角和规律表示出来？

生：（n-2）×180°。

在这个环节中，学生通过类比迁移自主探究了多边形的内角和公式，在这个过程中，学生经历了由特殊到一般的数学归纳过程，有效地培养了思维能力。