随机环境中马氏链函数的极限性质

黄 敏万成高

(1.武汉学院信息工程学院,湖北 武汉430212)

(2.中南财经政法大学统计与数学学院,湖北 武汉430073)

(3.湖北大学数学与统计学学院,湖北 武汉430062)

1 引言

设(Ω,F,P)是一概率空间,(X,A)和(Θ,B)均为任意的可测空间,={ξn:n≥0}和={Xn:n≥0}分别是(Ω,F,P)上取值于Θ 和X的随机序列,{P(θ):θ∈Θ}是(X,A)上的一族转移函数,且假设对任意的A∈A,P(·;·,A)是B×A可测的,{K(·,·)}是(Θ,B)上的转移函数,且假设对任意B∈B,K(·,B)是关于B可测的.对任意序列记设这里Θj=Θ,Bj=B,j≥0.

如果对任意A∈A,n≥0,有

则称为随机环境中的马氏链,称为随机环境序列.若是一马氏序列,则称为马氏环境中的马氏链.

本文假设是一步转移概率为K(θ,B)的马氏链,对任意的E∈A×B,记Pn(E)=P((Xn,ξn)∈E).约定:文中出现的C总表示正常数,它在不同的地方可以代表不同的值.集合A的示性函数记为IA.

20世纪80年代初,Cogburn等人开始研究随机环境中马氏链的一般理论,取得了一系列深刻的结果[1-3].Orey[4]在Cogburn等人的研究基础上对随机环境中马氏链进行了深入的研究,并提出了一系列的问题,引起了众多概率论学者的广泛关注,使得随机环境中马氏链一般理论的研究成为国际上又一新的研究方向.国内学者对这一领域进行了深入的研究[5-9].目前,随机环境中马氏链的强大数定律这方面研究的相关文献比较多[10-13],如由李应求(2003)首先提出具有离散参量的马氏环境中马氏链函数的强大数定律,并且给出了直接加于链和过程样本函数上的充分条件.随后,郭明乐(2004)同样也研究了随机环境中马氏链的强大数定律.近年来,不同于李应求和郭明乐等人所研究的,吴艳蕾等人(2011)和宋明珠等人(2016)又分别研究了随机环境中马氏链的强大数定律成立的一系列充分条件.大家知道,极限定理一直是经典马氏链理论研究中的热门课题,取得的结果已十分深入.鉴于此,本文研究了随机环境中马氏链函数的极限性质,给出了随机环境中马氏链函数强大数定律成立的一系列充分条件.本文结构安排如下:首先,本文定理1给出了马氏序列的强大数定律成立的两个充分条件且得到了之前学者的相似结论;然后,在定理1的基础上对偶函数列gn(x)取适合的函数,即可得到之前学者的一系列充分条件,故此充分条件较已有结论相对弱一些,从而推广了之前学者的一系列充分条件;最后,利用本文所给出的充分条件重新给出了随机环境中马氏链函数强大数定律成立的一系列充分条件.因此,本文拓宽了已有结论的适用范围.

2 主要结果及证明

引理1[11]设为随机环境中的马氏链,则是马氏链.

定理1设{(Xn,Yn):n≥0}是(Ω,F,P)上取值于X×Y上的马氏序列,{fn:n≥0}是(X,A)可测函数列.{gn(x),n≥0}为R上的偶函数序列,在区间(0,∞)上取正值,且对任意的n≥0,存在λ＞0,使得下述条件之一成立

(i)gn(x)在(0,∞)内单调不减,当0＜x≤1时,gn(x)≥λxθ(0＜θ≤1),且Efn(Xn)=0,n≥0;

同时对于正常数序列{an,n≥0},满足an↑∞,有

则对任意的k≥1,有

及

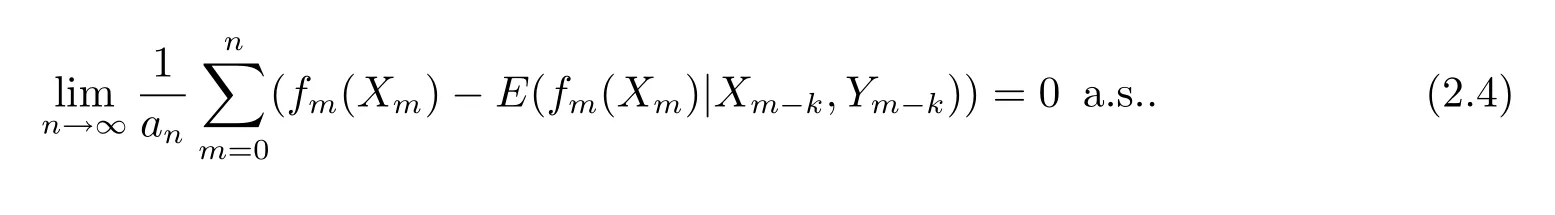
这里约定:对任意的k≥1,X-k≡0,Y-k≡0.

证先考虑k=1的情况.在条件(i)下,当|fn(Xn)|＞an时,由于gn(x)在(0,∞)内单调不减,且有gn(1)≥λ.从而

在条件(ii)下,当|fn(Xn)|＞an时,利用gn(x)≥λxβ(β≥1,x＞1),可知

由(2.5)式或(2.7)式知

即P(|fm(Xm)|＞am:i.o.)=0,因而

由(2.6)式或（2.8）式知

记

由{(Xn,Yn),n≥0}的马氏性,易知{Zn,Bn,n≥0}为鞅差序列.在条件(i)下,由鞅差序列的正交性知

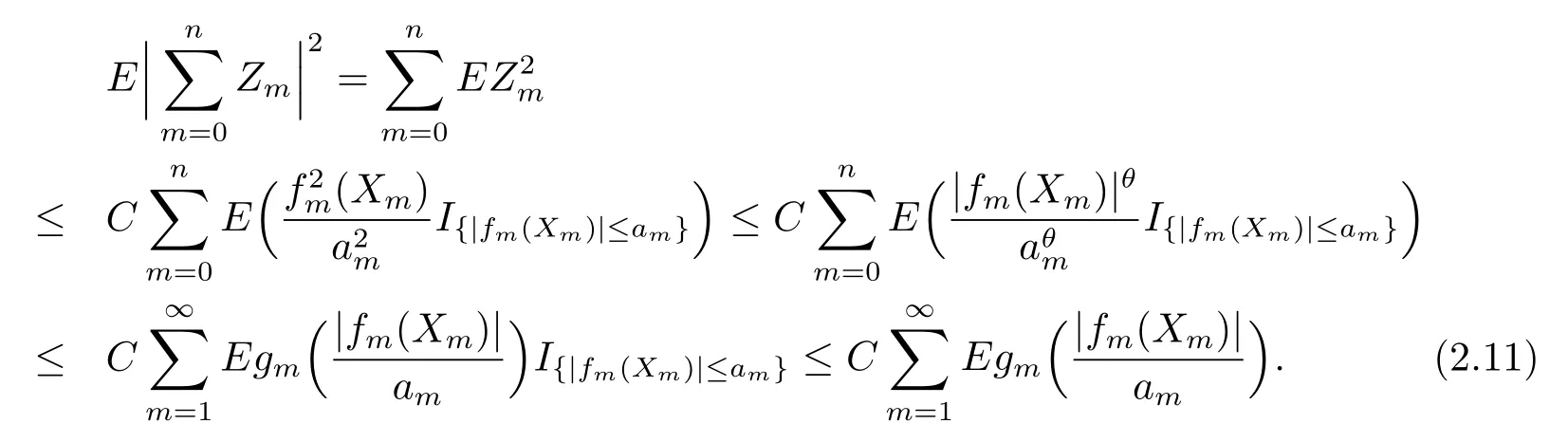
在条件(ii)下,同样有

下面再考虑k＞1的情形.由{(Xn,Yn):n≥0}的马氏性易知,对任意的n=1,2,3,···,k-1,{(Xmk+n,Ymk+n):m≥0}是马氏链,由(2.2)式显然有

因此对任意的n=1,2,3,···,k-1,有

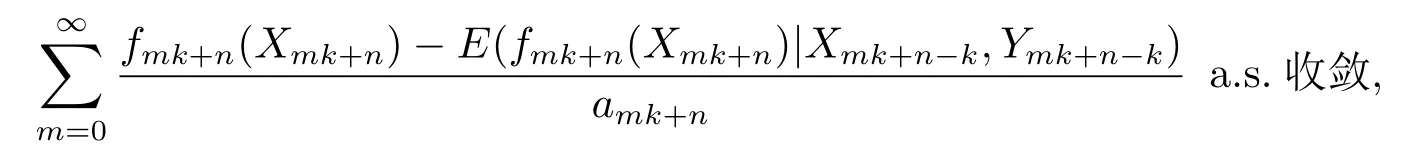
从而

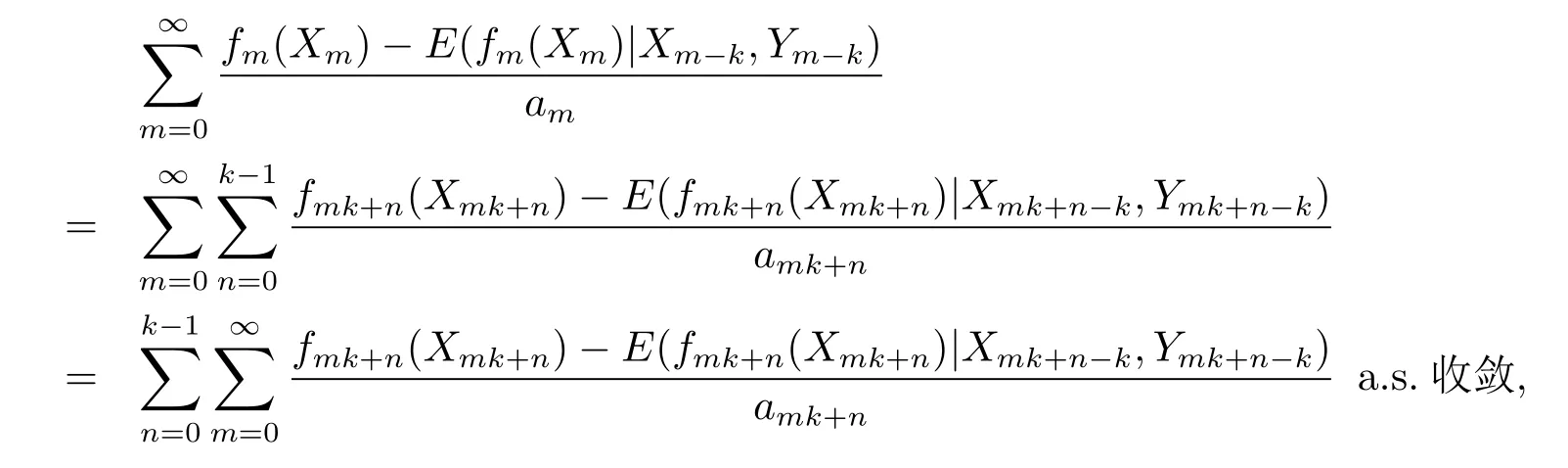
亦即(2.3)式对k＞1成立,又由Kronecker引理知(2.4)式对k＞1也成立.

注本文定理1的充分条件中,对偶函数列gn(x)取适合的函数时,例如当0＜r＜1时,gn(x)=|x|r/(1+|x|r);当1≤r≤2时，gn(x)=|x|r/(1+|x|r-1),即可得到类似于之前学者已有结论.较之前学者已有结论,如文献[12]的定理1和文献[13]的定理1,本文的推论1和推论2都是在定理1的基础上对gn(x)取不同的函数,即可得已有结论.因此本文所给出的随机环境中马氏链函数强大数定律成立的两个充分条件拓宽了已有结论的适用范围.

推论1设{(Xn,Yn):n≥0}是(Ω,F,P)上取值于X×Y上的马氏序列,{fn:n≥0}是(X,A)可测函数列.{φn(x),n≥0}为R上的偶函数序列,在区间(0,∞)上取正值,且对任意的n≥0,下述条件之一成立

(iii)φn(x),x/φn(x)在(0,∞)内不减,且Efn(Xn)=0,n≥0;

(iv)φn(x)/x,x2/φn(x)在(0,∞)内不减.同时对于正常数序列{an,n≥0},满足an↑∞,若有则有(2.3)和(2.4)式成立.

证取gn(y)=φn(xy)/φn(x),对任意的x∈(0,∞),y∈R,则有

且gn(y)为在(0,∞)内取正值的偶函数.

同时,在条件(iii)下,gn(y)满足定理1的条件(i),在条件(iv)下,gn(y)满足定理1的条件(ii),而且于是由定理1知,推论1的结论成立.

推论2设{(Xn,Yn):n≥0}是(Ω,F,P)上取值于X×Y上的马氏序列,{fn:n≥0}是(X,A)可测函数列.{an,n≥0}是正常数列,满足an↑∞,若有下述条件之一成立

则有(2.3)和(2.4)式成立.

证当条件(v)成立时,取gn(x)=|x|r/(1+|x|r),0＜r＜1;当条件(vi)成立时,取1≤r≤2.那么对任意的n≥0,gn(x),均为偶函数,且在(0,∞)内取正值,不减.同时分别有

若条件(v)被满足,则

若条件(vi)被满足,则

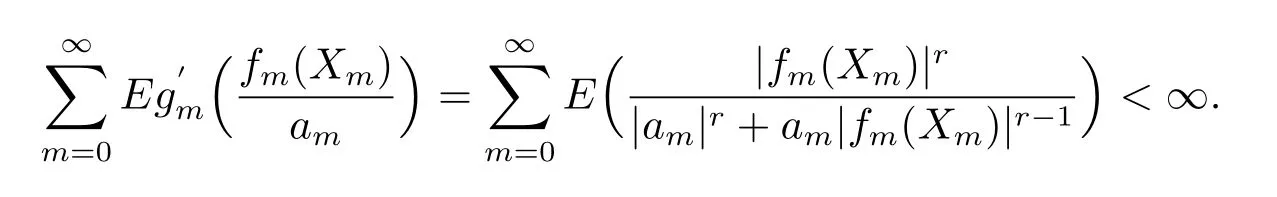
于是由定理1知推论2成立.

定理2设为随机环境中的马氏链,{fn:n≥0}是(X,A)上可测函数序列,0＜an↑∞,如果定理1(或推论1、推论2)条件成立,则对任意的k≥1,有

及

证由引理1知是马氏链,从而由定理1(或推论1、推论2)知(2.13)和(2.14)式均成立.

定理3在定理2的条件下,则对任意的k≥1,有

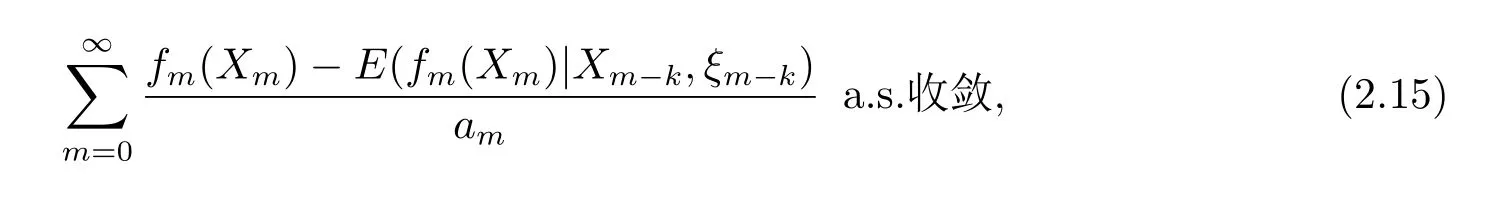
及

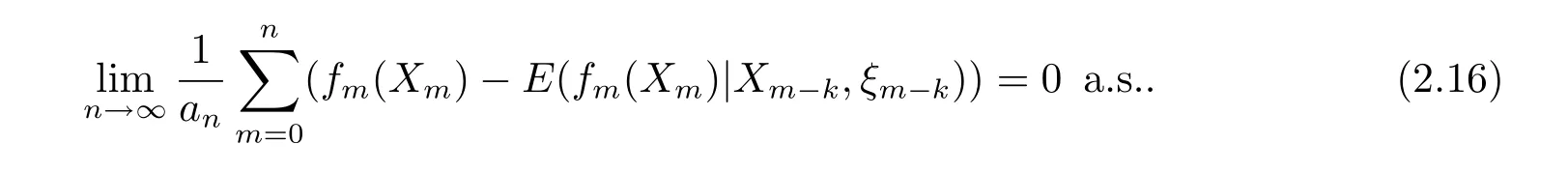
证同文献[11]中推论2的证明.

定理4在定理3的条件下,若存在C＞0,对任意的n≥0,都有n/an≤C,且

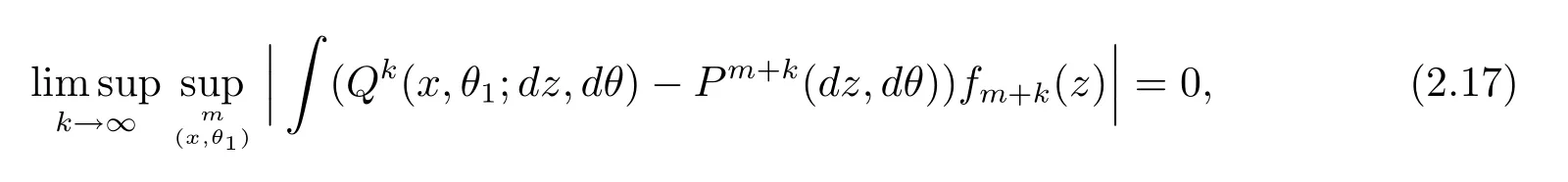
则

证由于定理3的条件满足,从而(2.16)式成立.又由于

因此欲证(2.18)式成立,只需证

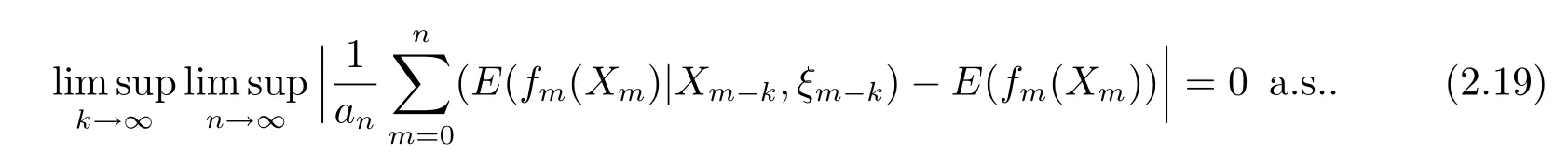
由于{(Xn,ξn):n≥0}是一步转移概率为Q(x,θ;A×B)=K(θ,B)P(ξ;x,A)的马氏链,故有

上述第一个等式是由于m＜k时,有E(fm(Xm)|Xm-k,ξm-k)=E(fm(Xm)a.s..从而由(2.17)式知(2.19)式成立,继而(2.18)式成立.