BIFURCATION AND POSITIVE SOLUTIONS OF A p-LAPLACIAN PROBLEM
LUO Hua
(1.School of Economics and Finance,Shanghai International Studies University,Shanghai201620,China)
(2.School of Mathematics,Dongbei University of Finance and Economics,Dalian116025,China)
Abstract:This paper studies a p-Laplacian problem with non-asymptotic nonlinearity at zero or infinity.By using the bifurcation and topological methods,the existence/nonexistence and multiplicity of positive solutions are obtained.The previous results of the existence of positive solutions are enriched and generalized.
Keywords: bifurcation;positive solution;p-Laplacian;topological method
1 Introduction
Consider the followingp-Laplacian problem

whereλis a nonnegative parameter,Ω is a bounded domain of RNwith smooth boundary∂Ω,p∈(1,+∞)andf:[0,+∞)→[0,+∞)is some given continuous nonlinearity.We also assume thatf(s)>0 fors>0 and there existf0,f∞∈[0,+∞]such that

whereφp(s)=|s|p-2s.
Iff0,f∞∈(0,+∞)withf0/=f∞,it follows from Theorem 5.1–5.2 in[1]that problem(1.1)has at least one positive solution for anyλ∈(min{λ1/f0,λ1/f∞},max{λ1/f0,λ1/f∞}),whereλ1is the first eigenvalue of problem(1.1)withf(s)=φp(s).Here we study the cases off0/∈(0,+∞)orf∞/∈(0,+∞).Iffis superlinear,we also require thatfsatisfies the following subcritical growth condition

for someq∈(p,p*)and positive constantC,where

is the Serrin’s exponent(see[2]).
Our main result is the following theorem.
Theorem 1.1(a)Iff0∈(0,+∞)andf∞=0,problem(1.1)has at least one positive solution for everyλ∈(λ1/f0,+∞).
(b)Iff0∈(0,+∞)andf∞=+∞,problem(1.1)has at least one positive solution for everyλ∈(0,λ1/f0).
(c)Iff0=0 andf∞∈(0,+∞),problem(1.1)has at least one positive solution for everyλ∈(λ1/f∞,+∞).
(d)Iff0=f∞=0,there existsλ*>0 such that problem(1.1)has at least two positive solutions for anyλ∈(λ*,+∞).
(e)Iff0=0 andf∞=+∞,problem(1.1)has at least one positive solution for anyλ∈(0,+∞).
(f)Iff0=+∞andf∞=0,problem(1.1)has at least one positive solution for anyλ∈(0,+∞).
(g)Iff0=+∞andf∞∈(0,+∞),problem(1.1)has at least one positive solution for anyλ∈(0,λ1/f∞).
(h)Iff0=f∞=∞,there existsλ*>0 such that problem(1.1)has at least two positive solutions for anyλ∈(0,λ*).
2 Proof of Theorem 1.1
We first have the following two nonexistence results.
Lemma 2.1Assume that there exists a positive constantρ>0 such that
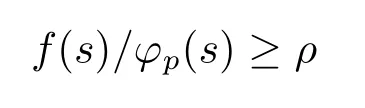
for anys>0.Then there existsξ*>0 such that problem(1.1)has no positive solution for anyλ∈(ξ*,+∞).
ProofBy contradiction,assume thatun(n=1,2,···)are positive solutions of problem(1.1)withλ=λn(n=1,2,···)such thatλn→+∞asn→+∞.Then we have thatλnf(un)/φp(un)>λ1fornlarge enough.By Theorem 2.6 of[3],we know thatunmust change sign in Ω fornlarge enough,which is a contradiction.
Lemma 2.2Assume that there exists a positive constantϱ>0 such that
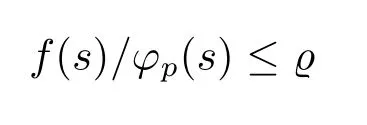
for anys>0.Then there existsη*>0 such that problem(1.1)has no positive solution for anyλ∈(0,η*).
ProofSuppose,on the contrary,that there exists one positive solutionu.Then we have that

which implies thatλ≥λ1/ϱ.
Let
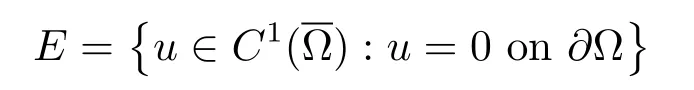
with the usual norm

Set
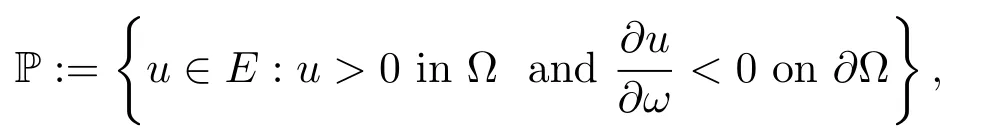
whereωis the outward pointing normal to∂Ω.
Proof of Theorem 1.1(a)From Lemma 5.4 of[1],there exists a continuumCof nontrivial solutions of problem(1.1)emanating from(λ1/f0,0)such thatC⊂(R×P)∪{(λ1/f0,0)},meets∞in R×E.It suffices to show thatCjoins(λ1/f0,0)to(+∞,+∞).Lemma 2.2 implies thatλ>0 onCandλ=0 is not the blow up point ofC.
We claim thatCis unbounded in the direction ofE.Suppose,by contradiction,thatCis bounded in the direction ofE.So there exist(λn,un)∈Cand a positive constantMsuch thatλn→+∞asn→+∞and‖un‖≤Mfor anyn∈N.It follows thatf(un)/un≥δfor some positive constantδand alln∈N.Lemma 2.1 implies thatun≡0 fornlarge enough,which is a contradiction.Lemma 5.1 of[4]implies that the unique blow up point ofCisλ=+∞.Now the desired conclusion can be got immediately from the global structure ofC.
(b)It is enough to show thatCjoins(λ1/f0,0)to(0,+∞).Lemma 2.1 implies thatCis bounded in the direction ofλ.By virtue of Lemma 5.1 of[4],we know that(0,+∞)is the unique blow up point ofC.
(c)If(λ,u)is any solution of(1.1)with‖u‖0,dividing(1.1)by‖u‖2(p-1)and settingw=u/‖u‖2yield
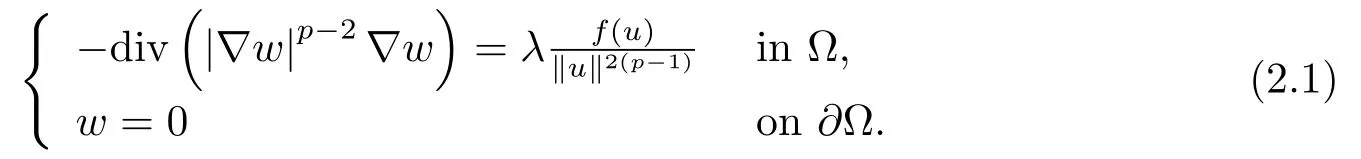
define
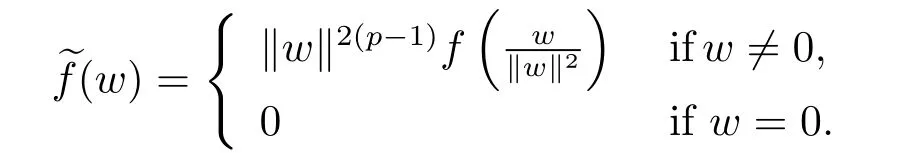
Then(2.1)is equivalent to

By doing some simple calculations,we can show thatApplying the conclusion of(a)and the inversionw→w/‖w‖2=u,we obtain the desired conclusion.
(d)define

and consider the following problem
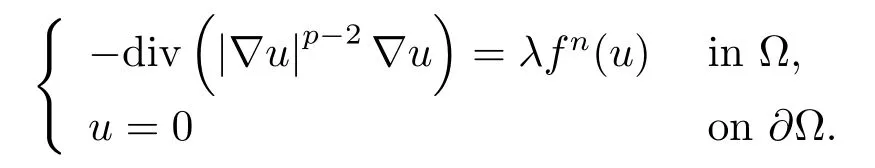
From Proposition 2 of[4],for each∈>0 there exists anN0such that for everyn>N0,Cn⊂V∈(C)withV∈(C)denoting the∈-neighborhood ofC.It follows that(nλ1,+∞)⊆Proj(Cn)⊆Proj(V∈(C)),where Proj(Cn)denotes the projection ofCnon R.So we have that(nλ1+∈,+∞)⊆Proj(C)for anyn>N0.Hence,we haveC{∞}/Ø.
Let

For any fixedn∈N,we claim thatCn∩S1=Ø.Otherwise,there exists a sequence(λm,um)∈Cnsuch that(λm,um)→(+∞,u*)∈S1with‖u*‖<+∞.It follows that‖um‖ ≤Mnfor some constantMn>0.It implies thatfn(um)/um≥δnfor some positive constantδnand allm∈N.Lemma 2.1 implies thatum≡0 formlarge enough,which contradicts the fact of‖v*‖ >0.It follows thatSinceone has thatC∩S1=Ø.Furthermore,set

For any fixedn∈N,byf∞=0 and an argument similar to that of(a),we have thatCn∩S2=Ø.Reasoning as the above,we have thatC∩S2=Ø.Hence,C∩(S1∪S2)=Ø.Takingz*=(+∞,0),we haveTherefore,we obtain thatC∩{∞}={z*,z*}.Clearly,is pre-compact.So Lemma 3.1 of[6]implies thatCis connected.By an argument similar to that of Theorem 1.3 of[4],we can show thatC∩([0,+∞)×{0})=Ø.Now the desired conclusion can be deduced from the global structure ofC.
(e)By an argument similar to that of(d),in view of the conclusion of(b),we can get the desired conclusion.
(f)By an argument similar to that of(c)and the conclusion of(e),we can prove it.
(g)By an argument similar to that of(c)and the conclusion of(b),we can obtain it.
(h)define

- 数学杂志的其它文章
- HYPOELLIPTIC ESTIMATE FOR SOME COMPLEX VECTOR FIELDS
- FAST AND SLOW DECAY SOLUTIONS FOR SUPERCRITICAL FRACTIONAL ELLIPTIC PROBLEMS IN EXTERIOR DOMAINS
- NORM STRUCTURES OF A FUZZY NORMED SPACE
- MODIFIED LAVRENTIEV REGULARIZATION METHOD FOR THE CAUCHY PROBLEM OFHELMHOLTZ-TYPE EQUATION
- 几类区域上不等维的边界唯一性定理
- 带固定效应空间误差面板数据模型的经验似然推断

