准静态侧向撞击下钢筋混凝土圆柱桥墩破坏模式判别

谢中友，潘建华

准静态侧向撞击下钢筋混凝土圆柱桥墩破坏模式判别

*谢中友1,2，潘建华3

（1.铜陵学院建筑工程学院，安徽，铜陵 244061；2.铜陵学院岩土工程研究所，安徽，铜陵 244061；3.合肥工业大学工业与装备技术研究院，安徽，合肥 230009）

当大质量车辆高速撞击桥墩时，产生的巨大撞击力可能导致桥墩损伤甚至破坏。本研究准静态侧向撞击下，钢筋混凝土圆柱桥墩的破坏模式。首先根据经典结构力学理论得到桥墩截面最大内力，结合钢筋混凝土圆形截面抗剪、抗弯承载力计算式，得到钢筋混凝土圆柱桥墩抗侧向撞击破坏的强度条件，最后得到剪切、弯曲、剪切弯曲三种破坏模式的判别标准。采用ABAQUS有限元软件对三种工况进行模拟研究，结果表明破坏模式判别标准具有很好的有效性。

钢筋混凝土；圆柱桥墩；侧向撞击；破坏模式

0 引言

随着交通基础设施快速建设，车辆撞击桥墩事故发生概率日渐增加[1-2]。车辆撞击桥墩常常引起桥梁部分或整体破坏[3-5]。据统计，1980至2012年期间，美国15%的桥梁破坏事故是由汽车撞击造成，在所有桥梁破坏成因中排名第三[6]。为此，2012年美国桥梁设计规范AASHTO-LRFD第六版大幅修订了相关技术标准，撞击力由1800 kN提高到2670 kN[7]。但我国2015年最新桥梁设计规范《公路桥涵设计通用规范（JTG D60-2015）》并未修订该部分技术标准，撞击力依然设为1000 kN[8]，说明车辆撞击桥墩问题在我国未能引起足够的重视。Abdelkarim等[9]研究认为，车辆侧向撞击下，桥墩破坏模式以剪切破坏为主。Zhou等[10]研究结果表明，当车辆冲击动能较小时，桥墩发生弯曲-剪切破坏，反之，桥墩发生剪切破坏。最近的研究发现桥墩还存在弯曲和冲切两种破坏模式[11][11]。对车辆侧向撞击下桥墩的动态响应及其破坏模式虽然已有大量研究[12-17]，但绝大多数均采用有限元模拟的方法。简洁有效的理论模型未见报道。

桥墩在受到外力撞击时，可能发生剪切、弯曲等多种破坏模式，具体发生的破坏模式类别主要与桥墩自身的结构形式和材料性能有关。本文建立了各种破坏模式下桥墩的结构承载力计算模型，通过比较不同破坏模式下的结构承载力，判定桥墩结构最先可能发生的破坏模式。同时，将理论计算的结构承载力与桥梁规范设计撞击力进行比较，进而判断特定桥墩结构是否满足设计规范要求。通过选取几个工程算例，发现理论计算的结构承载力与有限元计算结果具有良好的一致性，可以作为桥墩抗撞击设计的有效参考。

1 破坏模式判别标准理论分析

1.1 钢筋混凝土圆形截面承载力计算

1.1.1 斜截面抗剪强度

钢筋混凝土圆形截面的斜截面抗剪强度计算公式有很多，根据美国桥梁设计规范[7]，截面总抗剪强度n由混凝土抗剪c和箍筋抗剪s两部分组成，即

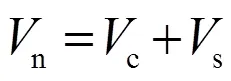
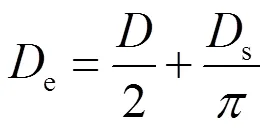
1.1.2 正截面抗弯强度

对于钢筋混凝土圆形截面正截面抗弯承载力，常生福基于《混凝土结构设计规范》（GB 50010-2002）给出如下简化计算公式[18]

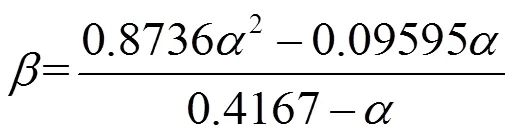
其中，s为纵向钢筋重心所在圆周的半径。A为混凝土圆柱截面面积，As为纵向钢筋的截面面积总和。c取为混凝土28天抗压强度，y为纵向主筋屈服强度。为对应于受压区混凝土截面的圆心角（弧度）与2π的比值，由方程(8)反算确定。

1.2 侧向加载下桥墩内力简化计算

图1给出了桥墩侧向加载受力示意图，其中为墩身高度，为车辆撞击点高度，为横向撞击力。桥墩底端一般与桩基固结，简化为固支边界。由于上部结构的约束，墩顶横向一般难以产生位移。另外，已有研究表明，墩顶压力对车墩撞击作用影响较小[9]，因而忽略轴力。

图1 圆柱桥墩侧向加载受力示意图

根据经典结构力学理论，桥墩截面将产生剪力和弯矩两种内力，其最大值计算式为

其中s为剪力，A，C分别为墩底和力作用点截面的弯矩。

对相关参数进行无量纲化，记

则剪力和弯矩计算式分别简化为

为更直观地了解剪力、弯矩随撞击点高度的变化特点，分别将其绘于图2和图3中。可以看出，剪力随撞击点高度增大逐渐减小，而两个截面的弯矩都存在峰值，撞击点相对高度较小时底端截面弯矩最大，超过一定限值（约为0.586）后撞击点截面弯矩最大。对于撞击点高度，中国规范定为1.2 m[8]，而美国最新规范提高到1.5 m[7]。考虑到车辆行驶需要，桥下净空一般至少达到4.5 m以上，此时底端为最大弯矩所在截面。

图2 剪力随加载点高度变化曲线

图3 弯矩随加载点高度变化曲线

1.3 截面破坏模式判别标准

按照强度设计一般原理，当截面实际内力小于截面承载能力时，截面不会破坏破坏，即

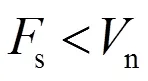
为方便直接对撞击力进行比较判别，做如下定义

其中，[V]和[M]分别定义为抗剪容许载荷和抗弯容许载荷。由此，方程(17)、方程（18）等效成如下形式

判别式方程(19)、方程(20)即为钢筋混凝土圆柱桥墩抗侧向撞击的强度条件。当上述强度条件其中之一或全部不能满足时，圆柱桥墩将发生相应的破坏破坏模式，如表1所列。

表1 圆柱桥墩破坏模式判别标准

2 圆柱桥墩侧向加载有限元模拟

2.1 有限元模型构建

为检验破坏模式判别条件的有效性，采用ABAQUS软件对圆柱桥墩侧向加载进行有限元模拟。模型中，采用环形质量块对桥墩侧面进行位移加载，与桥墩接触范围按文献[19]进行取值，高度方向设为0.25 m，环向设为25%的桥墩周长。中国现行规范，加载点离地高度为1.2 m[8]，本模型按美国现行规范，加载点离地高度取为1.5m[7]。模型中钢筋采用桁架单元（Truss），材料性能根据GB50010-2015混凝土结构设计规范，如表2所列。混凝土材料采用塑性损伤模型（Concrete damaged plasticity），混凝土材料参数采用Abaqus Verification Guide中实例数据，弹性模量26.48 GPa，泊松比0.167，混凝土塑性损伤模型数据列于表3，压缩拉伸性能具体数据见Abaqus Verification Guide。有限元模型计算了3种工况，详细数据见表4所列。桥墩边界条件与图1一致，即下端固支，顶端简支。有限元模型图见图4所示。

表2 钢筋力学参数

表3 混凝土塑性损伤模型数据

表4 有限元计算工况参数选取

图4 有限元模型图

2.2 静态撞击力分析

车辆撞击桥墩是一个典型的动态冲击问题，动态撞击力与车辆工况（包括车辆质量、车辆速度、车身材料结构）和桥墩工况（包括桥墩结构、材料及边界条件）等有关。各国规范为了设计应用方便，均采用等效静态撞击力作为控制指标，其中欧洲规范的等效静态撞击力取为车辆工况的函数，而美国和中国规范分别采用2670 KN和1000 KN两个不变的常量[7-8]。有限元模型采用位移加载方式，加载速度1m/s，模拟准静态加载下的结构响应。

图5给出了有限元模型计算得到的准静态撞击力随加载点位移的变化关系。可以看出，在加载初期，撞击力存在一个很大的峰值，随后很快下降至一个相对平稳的平台阶段。撞击力峰值对应于结构的弹性响应，平台阶段对应一定破坏模式下的破坏撞击力。对于工况1，从图5（a）可以看出，[F]＜[F]，可以认为该工况将优先发生剪切破坏，与有限元计算结果基本一致。另外，[F]＜[F]＜美国规范撞击力，[F]＜中国规范撞击力＜[F]，因此，按照美国规范该桥墩将发生剪切和弯曲破坏，而按中国规范该桥墩只发生剪切破坏。对于工况2，图5（b）结果表明[F]≈[F]，该桥墩将几乎同时发生剪切、弯曲破坏，与有限元计算结果基本一致。另外，根据美国规范和中国规范，该工况均将发生剪切弯曲破坏。对于工况3，图5（c）结果说明[F]＞[F]，该工况优先发生弯曲破坏模式。另外，按照美国规范该桥墩将发生剪切和弯曲破坏，而按中国规范该桥墩只发生弯曲破坏。

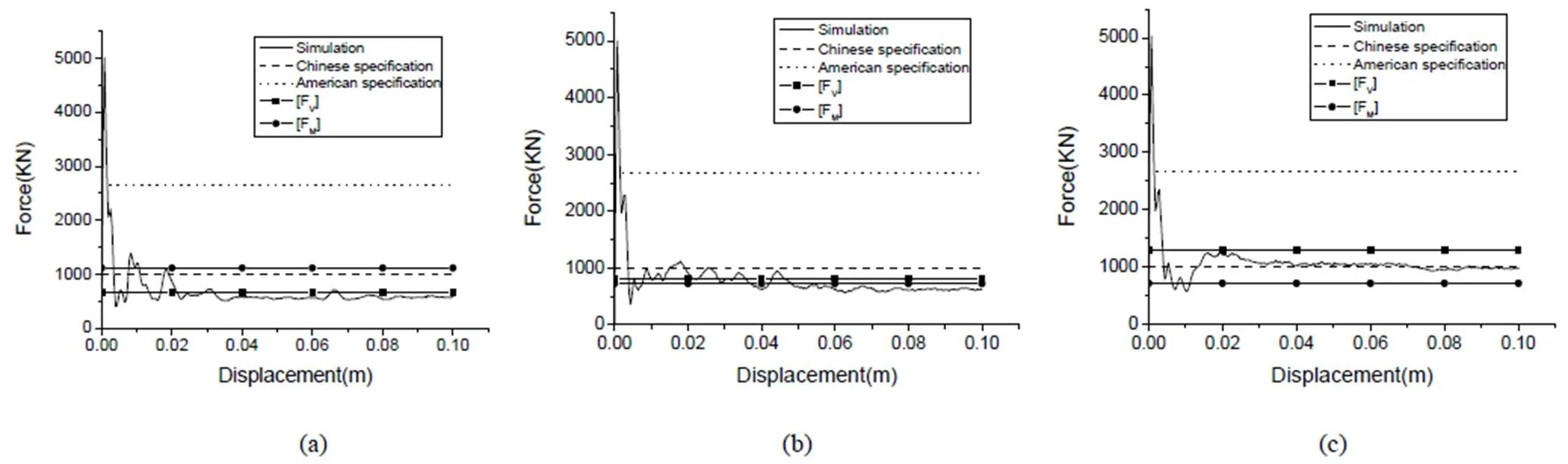
图5 侧向撞击力随加载位移变化曲线：（a）工况1；（b）工况2；（c）工况3

2.3 变形图分析

为进一步明确三种工况的破坏模式，可观察有限元计算得到的变形图。图6给出了三种工况混凝土的等效塑性应变云图。从图6（a）可以看出，工况1存在一个明显的剪切面，结构发生了明显的斜截面剪切变形破坏，因此工况1属于剪切破坏模式。图6（b）可以看出，工况2的混凝土柱也存在一个明显的剪切面，同时桥墩发生了一定的弯曲变形，因此工况2属于剪切弯曲破坏模式。图6（c）图所示的工况3，未产生明显的剪切面，底端截面应变较大，结构产生了明显的弯曲变形，因此工况3属于弯曲破坏模式。总之，对于三种工况的破坏模式，根据有限元计算得到的变形图和本文的破坏模式判别标准，两种途径得出的结论都是一致的，说明本文的破坏模式判别标准是有效的。

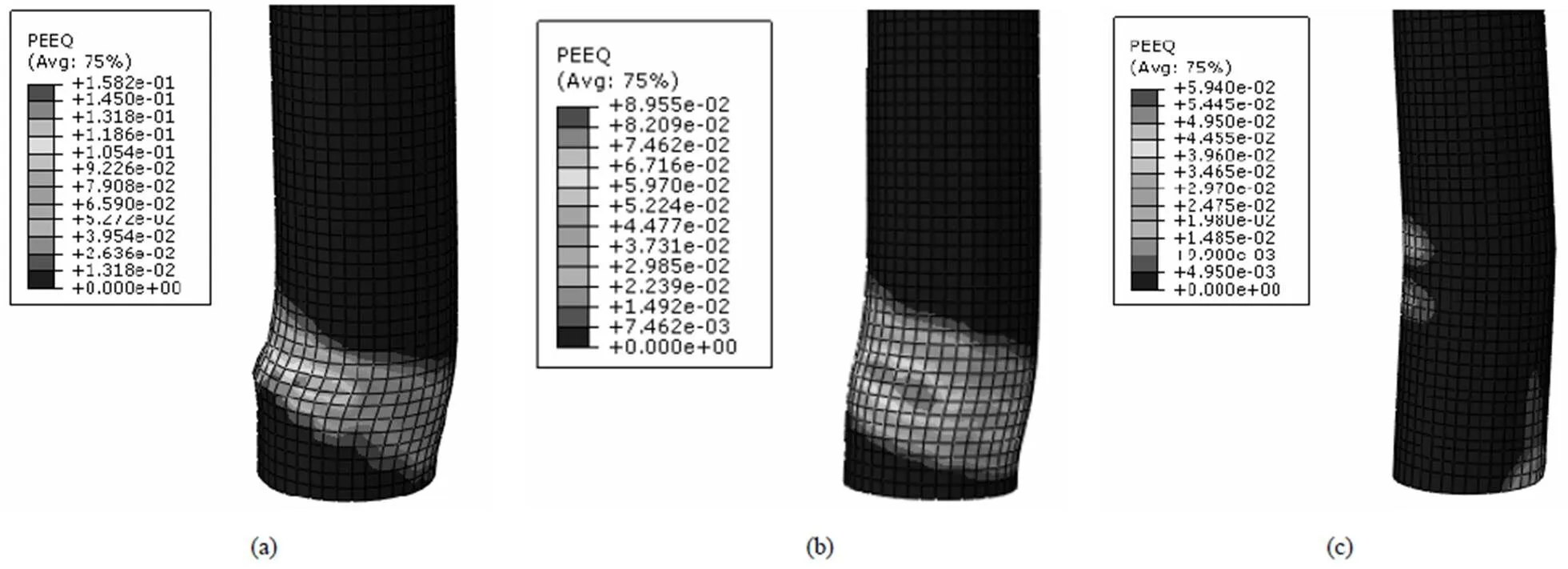
图6 等效塑性应变分布云图：（a）工况1；（b）工况2；（c）工况3

3 结论

钢筋混凝土桥墩在车辆撞击等侧向载荷作用下会发生剪切、弯曲、剪切弯曲三种破坏模式。本文根据经典结构力学理论得到桥墩截面最大内力，结合钢筋混凝土圆形截面抗剪、抗弯承载力计算式，得到钢筋混凝土圆柱桥墩抗侧向撞击的强度条件，进而得到三种破坏模式的判别标准。采用ABAQUS有限元软件对三种工况进行模拟研究，结果表明两种途径得到的结论一致，破坏模式判别标准具有很好的有效性，可作为桥墩设计的有效参考。

[1] El-Tawil S, Severino E, Fonseca P. Vehicle collision with bridge piers[J]. Journal of Bridge Engineering 2005;10(3):345-53.

[2] Tsang H H, Lam N T K. Collapse of reinforced concrete column by vehicle impact[J]. Computer Aided Civil and Infrastructure Engineering , 2008,23:427-436.

[3] Hartik I E, Shaaban A M, Gesund H, et al. United States bridge collapses[J]. Journal of Performance of Construction Facilities, 1990, 4(4):272-277

[4] Buth C E, Williams W F, Brackin MS, et al. Analysis of large truck collisions with bridge piers: phase 1[J]. Texas Department of Transportation Research and Technology Implementation Office,2010, 9:4973-1.

[5] Agrawal A K. Bridge vehicle impact assessment: final report[C]. University transportation research center and New York State Department of Transportation, 2011.

[6] Lee G C, Mohan S, Huang C, et al. A study of US bridge collapses (1980–2012) [C]. MCEER technical report 13-0008. Buffalo (NY), 2013.

[7] Aashto-lrfd. Bridge design specifications – customary US units[M]. Sixth ed. Washington: American Association of State Highway and Transportation Officials; 2012

[8] 中华人民共和国行业标准. 公路桥涵设计通用规范(JTG D60-2015)[S]. 北京：人民交通出版社,2015.

[9] Abdelkarim O, Elgawady M A. Performance of bridge piers under vehicle collision[J]. Engineering Structures, 2017, 140: 337-352.

[10] Zhou D, Li R, Wang J, et al. Study on Impact Behavior and Impact Force of Bridge Pier Subjected to Vehicle Collision [J]. Shock and Vibration, 2017, 18: 1-12.

[11] Tin V Do, Thong M Pham, Hong Hao. Dynamic responses and collapse modes of bridge columns under vehicle collision [J]. Engineering Structures , 2018, 156: 243-259.

[12] Tsang Hing Ho. Collapse of Reinforced Concrete Column by Vehicle Impact [J]. Computer-Aided Civil and Infrastructure Engineering, 2008 , 23 (6) :427-436.

[13] 张国兵,杜晓雷. 跨越高速公路桥墩受汽车撞击力作用分析[J]. 公路交通科技：应用技术版,2010 (8)：241-243,250.

[14] 裴小吟,文传勇,张永水.城市桥梁被车辆撞击后损伤分析[J].重庆交通大学学报:自然科学版,2011,30 (1)：19-21.

[15] 崔堃鹏,夏禾,夏超逸,等.汽车撞击桥墩瞬态撞击力的等效静力计算[J].振动与冲击,2014,33(4):48-53.

[16] Abdelkarim O I, Elgawady M A. Performance of hollow-core FRP-concrete-steel bridge columns subjected to vehicle collision. Engineering Structures, 2016, 123: 517-531

[17] Chen L, Xiao Y, El-Tawil S. Impact Tests of Model RC Columns by an Equivalent Truck Frame [J]. Journal of Structural Engineering, 2016 , 142 (5) : 04016002

[18] 常生福. 圆形截面钢筋混凝土受弯构件正截面承载力的简化计算[J].中国港湾建设,2010(2):15-17 .

[19] Thilakarathna H M I, Thambiratnam D P, Dhanasekar S, et al. Numerical simulation of axially loaded concrete columns under transverse impact and vulnerability assessment [J]. International Journal of Impact Engineering, 2010, 37 (11) : 1100-1112

Judgment of collapse modes of reinforced concrete cylindrical piers under quasi-static lateral impact

*XIE Zhong-you1,2，PAN Jian-hua3

(1.College of Architectural Engineering, 2.Institute of Geotechnical Engineering, Tongling University, Tongling, Anhui 244061, China; 3.Institute of Industry & Equipment Technology, Hefei University of Technology, Hefei, Anhui 230009, China)

When a heavy vehicle at a high velocity impacts a bridge pier, the large reaction force generated could cause the pier damage and even collapse. Judging standards for the collapse modes are investigated in the paper.The maximum internal forces are derived based on classical elastic theory, and the strength conditions of lateralimpact collapse of reinforced concrete cylindrical piers are obtained according to previous formulations. Finally, the judging standards for the three collapse modes such as shearing, bending and shearing-bending are obtained. In addition, by using ABAQUS finite element code, three cases are simulated and the results demonstrate good agreement with the models predicted.

Reinforced concrete; Cylindrical piers; Lateral collision; Collapse modes

TU375.3

A

10.3969/j.issn.1674-8085.2020.04.015

1674-8085(2020)04-0077-06

2019-12-03；

2020-05-21

安徽省高校省级自然科学研究重点项目（KJ2018A0481）；中央高校基本科研业务费专项基金（PA2019GDPK0054）

*谢中友(1976-)，男，安徽怀宁人，副教授，博士，主要从事工程结构力学性能及安全防护研究(E-mail: zhyxie@126.com);

潘建华(1981-)，男，江苏盐城人，副教授，博士，主要从事承压设备安全评估研究(E-mail:panjianhua_123@163.com).