具有通信时滞的多无人飞行器系统编队控制研究①

张 潇 姜玉莲

(长春工业大学电气与电子工程学院 长春 130012)

0 引 言

近年来，由于多智能体系统在各领域的广泛应用，使得人们对多智能体系统协调控制的研究兴趣不断增加[1-4]。其中，编队控制作为该领域的重点研究方向之一，在飞行器、车辆、机器人等领域[5-7]得到了普遍的应用。无人飞行器主要分为无人机和卫星两类，其中卫星集群主要有成本低、测量精度高、容错率低等优点[8]。

一般来说，编队控制的主要问题是设计合适的控制协议，达成编队目标使各个智能体之间能够实现和保持预定的几何形状，完成相应的合作任务，如监视、勘探、搜索和救援、运送大型物体和控制卫星阵列等。编队控制主要有基于行为(behavior-based)法[7]、虚拟结构(virtual structure)法[9]和领导跟随(leader-following)法[10]。基于行为法定义了无人飞行器运动的一系列基本行为，通过综合行为实现运动控制。该方法有明确的队形反馈，但是对群体的行为没有明确意义，无法保证系统稳定性。虚拟结构法将整个编队队形看作刚体，每个无人飞行器与刚体上的点进行对应。该方法无法根据环境的变化改变队形，系统灵活性不足。领导跟随法通过引入“领导者”，从而让无人飞行器系统收敛到一个特定的轨迹[11]。该方法数学分析简单，队形易保持，系统的稳定性有保证，因此被广泛应用。文献[12]基于一致性算法实现了多航天器系统的编队飞行。文献[13]针对多无人飞行器系统，提出了一致性理论和分散式模型预测控制。文献[14]通过领导跟随法和人工势场法，解决了多自治水下机器人(autonomous underwater vehicle, AUV)编队的避障问题。文献[15]基于雁群行为设计了一种控制协议，实现了多无人飞行器编队重构。

多无人飞行器系统中，信息交互是保证多无人飞行器编队安全稳定控制的前提，由于信息传输和处理速度有限，相邻飞行器之间的交互不可避免地存在时滞，特别是通信时滞。当通信时滞较大时，很可能因为飞行器无法完成正常的信息交流从而导致编队失败，因此研究具有通讯时滞的编队控制具有十分重要的现实意义[16]。

本文主要研究了有向通信网络拓扑结构下，带有通信时滞的无人飞行器系统的编队控制问题。首先根据多智能体一致性理论提出多无人飞行器编队控制协议，然后利用负矩阵分析法给出了控制参数矩阵的特征值的取值范围，通过Lyapunov稳定性理论得到系统稳定的充分条件，并求解线性矩阵不等式(linear matrix inequality， LMI)求得通讯时滞的最大值，最后通过仿真实验验证了本文方法的有效性。

1 问题描述

1.1 图论基础

有向图G=(ν,ε,A)包含n个节点，表示n个多无人飞行器，其中ν={v1,v2,…,vn}表示节点集合，ε⊆ν×ν为图G边的集合，图G边的权值矩阵矩阵为A=[aij]，当(vi,vj)∈ε，且个体j能直接获得个体i的信息时，aij=1；若(vi,vj)∉ε，则aij=0。图G的Laplacian矩阵为L=(lij)，其中，

在有向图中，如果存在一个节点使得任意节点到这个节点都有有向路径，则称其为强连通图。

记H=L+D，其中D是对角矩阵，当领导者信息能被跟随者接收时，di=1；否则，di=0。下面的引理展现H的正稳定性与图G的连通性之间的关系。

引理1[1]当且仅当图G包含生成树，矩阵H=L+D是正稳定的。

1.2 系统模型

本文研究的多无人飞行器系统由n个无人飞行器和一个领导者无人飞行器构成，其中的无人飞行器是以文献[17]中的卫星集群系统作为本文的主要研究对象，第i个无人飞行器的动力学线性方程为

(1)

其中，xi、yi、zi表示第i个无人飞行器的位置分量信息；uxi、uyi、uzi为控制输入；ω0表示无人飞行器的角速率。

取ri=[xi,yi,zi]T表示第i个跟随者无人飞行器的位置信息，ui=[uxi,uyi,uzi]T表示第i个跟随者无人机的控制输入，这时，多无人飞行器系统模型式(1)可以改写为

(2)

其中，

领导者的动力学方程如下：

(3)

记(h0-hi)∈R3表示领导者与第i个跟随者的期望距离，ri(t)-r0(t)是领导者与第i个无人飞行器的实际距离。为明确编队控制目标，本文给出以下定义。

定义1当领导者与跟随者之间的距离误差和速度误差分别满足：

考虑到各个无人飞行器之间存在通讯时滞，在有向通信网络拓扑结构下，为实现多无人飞行器系统编队飞行，本文提出如下控制协议：

ui(t)=-A1[ri(t)-hi-r0(t)+h0]

+di[F1(r0(t-τ)-h0-ri(t-τ)+hi)

(4)

其中，F1，F2∈R3×3是控制参数矩阵且F1>0，F2>0，τ是相邻无人飞行器之间通讯时滞。

(5)

设复系数多项式R(z)=ζ0+ζ1z+…+ζnzn，令ζi∈C，i=0,1,…,n。将z=iϖ代入R(z)得R(iϖ)=α(ϖ)+iβ(ϖ)。其中，i为虚数单位，α(ϖ)，β(ϖ)∈R，首先给出引理2、3和4，以方便得到本文结果。

引理2[18]对于一个复系数多项式R(z)，当且仅当对应的多项式α(ϖ)，β(ϖ)是交错的并且α(0)β′(0)-α′(0)β(0)>0时，R(z)是赫尔维茨(Hurwitz)稳定。其中，α′(0)和β′(0)分别是α(0)和β(0)的导数。

引理3[19]若多项式α(ϖ)，β(ϖ)满足以下2个条件，则它们是交错的。

(1)α(ϖ)=0，β(ϖ)=0均只有互异的实根，即α1<α2<…<αk，β1<β2<…<βk′。

(2) 当|k-k′|≤1且当α(ϖ)=0，β(ϖ)=0的根满足以下3种情况：

引理4[20]设向量x，y∈Rn，对于任意的正定矩阵N∈Rn×n，有2xTy≤xTN-1x+yTNy。

2 编队控制稳定性分析

(6)

其中，H=L+D，F1,F2∈R3×3且F1>0，F2>0。

(7)

根据牛顿-莱布尼茨(Newton-Leibniz)公式有：

(8)

结合式(7)和(8)，可得到：

其中，

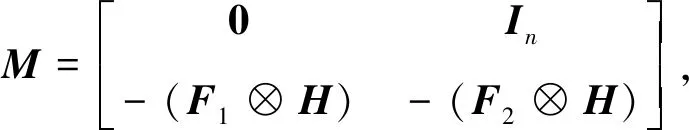
(9)

则M是Hurwitz稳定，其中θ是矩阵H的特征值。

证明取M的任意一个特征值z，则M的特征多项式为：

det(zI2np-M)

其中，H的第i个特征值用θi表示，f1，f2为F1，F2的任意特征值。令z=iϖ，代入R(z)得：

R(iϖ)=-ϖ2+f2[Re(θi)+iIm(θi)]iϖ

+f1[Re(θi)+iIm(θi)]

(10)

进而得到α(ϖ)=-ϖ2-Im(θi)f2ϖ+Re(θi)f1，β(ϖ)=Re(θi)f2ϖ+Im(θi)f1。

令α1<β1<α2得：

(11)

定理1对于系统式(11)，当控制参数矩阵的任意特征值f1和f2满足

(12)

且存在对称矩阵J>0，T>0，Q>0，同时J、T、Q∈R2n×2n满足：

(13)

则多无人飞行器系统式(11)能够实现编队飞行，其中，

η11=J[(In⊗A)-(H⊗B)]

+τ(In⊗A)TQ(In⊗A)

+[(In⊗A-(H⊗B)]TJ+T

η12=-τ(In⊗A)TQ(H⊗B)

η22=-T+τ(H⊗B)TQ(H⊗B)

η13=J(H⊗B)

证明构造新的Lyapunov函数为

求导得：

(14)

-2γT(t)J(H⊗B)γ(t-τ)

=-2γT(t)J(H⊗B)γ(t)

+τγT(t)J(H⊗B)Q-1[(H⊗B)J]Tγ(t)

-2γT(t)J(H⊗B)γ(t)

+τγT(t)J(H⊗B)Q-1[(H⊗B)J]Tγ(t)

+τγT(t)(In⊗A)TQ(In⊗A)γ(t)

-τγT(t)(In⊗A)TQ(H⊗B)γ(t-τ)

-τγT(t-τ)(H⊗B)TQ(In⊗A)γ(t)

+τγT(t-τ)(H⊗B)TQ(H⊗B)γ(t-τ)

-γT(t-τ)Tγ(t-τ)

+τ(In⊗A)TQ(In⊗A)

+[(In⊗A-(H⊗B)]TJ+T

+τJ(H⊗B)Q-1(H⊗B)J

3 仿真结果

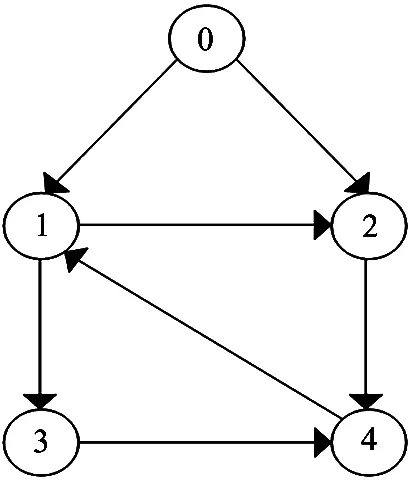
图1 通信拓扑图

(a) 通信时滞τ=0.1 s时的位置误差

(b) 通信时滞τ=0.1 s时的速度误差

图3 通信时滞τ=0.1 s时系统的编队运动轨迹

与跟随者无人飞行器的编队飞行轨迹，表明在t=0 s时刻，无人飞行器的位置随机分布，经过一段时间后4个跟随者无人飞行器追随领导者实现编队，并保持一个五边形的队形飞行，更为直观地验证系统在编队控制协议式(4)的作用下，能够渐近实现稳定性。

为进一步验证控制参数F1、F2和通信时滞对系统编队控制的重要性，本文另提供2部分仿真结果。

(2)当控制参数满足条件式(9)，设定通信时滞τ>τ0，即超出通信时滞上界τ0时，经过仿真计算，线性矩阵不等式(13)无可行解。

(a) 位置误差

(b) 速度误差

4 结 论

本文解决了有向通信拓扑结构下带有通信时滞的二阶多无人飞行器系统的编队控制问题，提出了新的编队控制律。基于图论、矩阵论和Lyapunov稳定性理论，利用负矩阵分析法将控制参数矩阵的特征值限定在一定范围内并给出了多无人飞行器系统能够稳定编队飞行的充分条件，且通过求解线性矩阵不等式，得到系统渐近实现编队时的最大通讯时滞允许上界。最后，通过仿真验证了所得理论结果的正确性和有效性，并证明了控制参数矩阵和通信时滞上界对多无人飞行器系统实现编队目标的重要性。