移动边缘计算中计算卸载与资源分配的联合优化策略①

龙 隆 刘子辰 石晶林 周一青 邱大伟 徐顺清

(*中国科学院计算技术研究所移动计算与新型终端北京市重点实验室 北京 100090) (**中国科学院大学 北京 100049)

0 引 言

随着移动通信的高速发展以及移动终端的快速普及，许多新型应用随之产生，如虚拟现实、增强现实以及自动驾驶等[1-5]。而这类需要具有低时延高可靠特点的应用对移动终端的计算能力提出较高要求。由于计算能力有限的移动终端在处理这类应用时将产生较高的时延进而影响终端用户的服务体验，因此如何降低应用处理时延、提升终端用户的服务体验是目前亟需解决的关键问题之一[6]。针对以上问题，移动云计算(mobile cloud computing，MCC)技术被提出。MCC的目标是将云端丰富的计算资源扩展至资源受限的移动终端，从而增强移动终端潜在的计算能力[7-10]。为实现该目标，移动终端需要将计算密集的任务通过无线接入的方式迁移至云服务器。尽管这种方式可以降低移动终端的负载但也存在明显的缺陷，即移动终端与云服务器较远的距离以及大量的终端业务请求将导致网络时延的增加，从而降低终端用户服务体验。

为了进一步降低网络时延，移动边缘计算(mobile edge computing，MEC)作为一种新的技术被提出。在MEC系统中，由基站与边缘服务器组成的服务节点就近为移动终端提供计算、通信与存储服务[11，12]。然而与云服务器相比，服务节点的计算资源有限，过多的计算任务将为服务节点带来额外的负载从而影响网络时延。因此为解决上述问题，需要设计一种新的MEC计算卸载与资源分配的联合优化策略。

目前，基于MEC的卸载策略与资源分配方面已有相关研究。文献[13]以最小化移动终端的能耗与时延为目标，对移动终端的卸载策略、计算资源以及传输功率进行联合优化。该研究优化了移动终端的计算能力、功耗以及卸载策略，但并未考虑云端计算资源的优化。文献[13]是在MCC应用场景下对时延与能耗进行研究，然而在该场景下移动终端与MCC较远的物理距离可能会导致额外的时延，进而影响用户的服务体验。文献[14]则提出了在MEC网络下一种基于排队论的低复杂度算法，该算法通过优化频谱资源与边缘服务器的计算资源以最小化移动终端的能耗与时延。文献[15]则提出了一种上行链路等功率分配方案，基于该方案对设备能耗进行优化。此外，由于博弈论是一种有效的分布式方法，因此广泛应用于解决MEC场景下的资源优化分配问题[16-18]。文献[19]则提出了基于博弈论的计算资源与频谱资源联合优化算法，解决了多终端用户的计算卸载与资源分配问题。尽管文献[14]与文献[19]采用不同的方法降低了终端的时延与能耗，但两者都忽略了下行频谱资源对终端时延的影响，而这在实际应用场景中并不总是成立的。例如在增强现实游戏应用场景中，移动用户将实时发送视频数据，而服务端将对收到的视频数据进行识别并经过渲染将视频返回至用户端。在此过程中，移动用户的任务时延不但受到数据上传、计算时延的影响，同样受到下行数据传输时延的影响，因此对于这类应用场景，下行链路资源的优化显得十分重要。

本文在MEC系统下，以最小化所有移动终端的任务时延为目标，提出一种基于博弈论的计算卸载与资源分配的联合优化算法(computation offloading and resource allocation game, CORAG)。该算法首先将所有移动终端的卸载决策与资源优化问题通过博弈模型进行表示并引入势博弈概念证明该模型具有纳什均衡性。随后在已知终端卸载决策的基础上，对上、下行频谱资源以及边缘服务器的计算资源进行联合优化并利用拉格朗日乘子法获取计算资源与频谱资源的最优解。最后，基于获得的最优解，利用迭代法得到所有移动终端的纳什均衡解。仿真结果表明，本文所提出的基于博弈论的计算卸载与资源分配算法与现有算法相比可以获取更低的时延，进而提升用户服务体验。

1 基于MEC的系统建模与问题描述

1.1 系统模型

MEC系统的网络框架如图1所示，该系统由1台边缘服务器与1个基站组成。

边缘服务器与基站可以为其覆盖范围内的N个移动终端提供计算与通信服务。其中多个移动终端的集合表示为L={i:i=1,2,…,N}，单个终端由i进行表示。为了防止终端间干扰，基站的频谱资源通过正交的方式分配给每个终端且总频谱带宽为B。假设每个终端只执行一个计算任务wi={si,mi,ci}，其中si表示输入数据的大小，mi表示计算结果数据的大小，ci表示一个任务所需中央处理器(central processing unit, CPU)循环总量。由于计算任务既可以本地执行也可以在边缘服务器执行，因此移动终端i的卸载决策由ai进行表示，其中Ai∈{0,1}且ai∈Ai。当Ai=1时，表示终端i将会选择将任务卸载至MEC服务器。Ai=0时，则表示任务在终端i执行。因此所有终端的卸载策略表示为A={Ai|Ai∈{0,1},i∈L}。

图1 MEC系统网络架构

1.2 通信模型

由于每个移动终端在执行任务时将会占用上行与下行的频谱资源，因此终端i的上行传输速率可以表示为

(1)

其中，ki为终端上传数据所占上行带宽百分比，Pi,B表示终端的发送功率，hi,B表示基站与终端间的信道衰落系数，d为终端与基站的距离，r为路径损耗，σ2为信道的噪声功率。同理下行传输速率表示为

(2)

其中，ξi为终端接收下行数据所占带宽百分比，hB,i表示为基站与终端间的信道衰落系数，PB为基站的发射功率。

1.3 计算模型

当移动终端将任务卸载至边缘服务器后，此时的任务时延主要由上行传输时延ti,u、下行传输时延ti,d、服务器计算时延ti,m以及回程链路时延ti,b4部分组成。由于基站与服务器之间是通过有线的方式进行连接，因此回程链路时延忽略不计。此外当移动终端选择在边缘服务器执行任务时，分配给移动终端的计算资源不能高于边缘服务器最大计算能力，其中边缘服务器的最大计算能力用fm表示。

(1)本地执行任务。当任务wi在本地执行时，计算时延表示为

(3)

其中，fi,l为移动终端的计算能力。因此终端i在本地执行任务的总时延表示为

Ui,l=ti,l

(4)

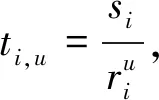
Ui,m=ti,u+ti,d+ti,m

(5)

1.4 问题形式化描述

由于不同任务所需的资源不同，为了满足所有移动终端的任务时延要求，在计算与通信资源约束条件下对终端的计算卸载决策A，上行频谱资源K，下行频谱资源P以及服务器计算资源F4个方面联合优化，其中优化目标可以表示为

(6)

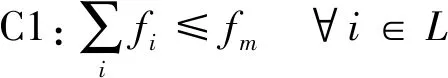
C4:fi,l≥0 ∀i∈L

C5:ai∈{0,1} ∀i∈L

其中F={fi,m:∑ifi,m≤fm,∀i∈L}，a=(a1,a2,…,an)，K={ki:∑iki≤1,∀i∈L}，P={ξi:∑iξi≤1,∀i∈L}。其中限制条件C1表示分配给所有移动终端计算资源总和小于等于服务器的计算能力，限制条件C2、C3表示分配给所有移动终端的上行与下行频谱资源的百分比，限制条件C4则表示终端的本地计算资源是非负的，C5表示为移动终端的卸载决策。此外由式(6)可以看出，由于ai为整型变量，因此问题式(6)为混合整型线性规划问题且为非凸的，因此很难得到直解。为了解决以上问题，本文提出了一种基于博弈论的计算卸载与资源分配算法。

2 基于博弈论的计算卸载与资源分配算法

博弈论是指博弈或者对弈过程中，通过考虑或预测参与人的实际行为从而优化参与者的决策。为了获取最优卸载策略，接下来将把上述问题建模为博弈模型。

2.1 博弈形式化表述

首先将问题式(6)通过博弈模型G={L,(Ai)i∈L,Wi}来表示，其中L为终端个数，Ai为终端的卸载策略，wi为终端i的时延效用函数。a-i=(a1,a2,…,ai-1,ai+1,…,aN)表示除了终端i以外其他终端的卸载决策。由于每个移动终端用户具有自私性，因此为了最小化所有终端的任务时延，所有参与者会对有限的计算资源、频谱资源进行竞争。因此在竞争条件下，每个移动终端的时延表示为

(7)

由于该模型具有纳什均衡的特性，即存在最优的卸载策略使得每个终端时延最低。因此在所有移动终端完成决策后，需要对卸载至服务器的移动设备进行通信与计算资源优化，而资源的优化目标可以表示为

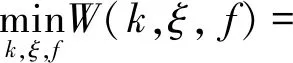
(8)

根据海塞矩阵很容易证明函数W(k,ξ,f)为凸函数，此外由于限制条件C1～C3是线性的，因此问题式(8)变为凸优化问题[20]。为了解决该问题，采用对偶的方法，相应的对偶函数表示为

(9)

可以看出式(9)分为2个部分。第1部分为内层函数，主要由变量k、f、ξ组成。第2部分为外层函数，其中变量μ、λ、θ为拉格朗日乘子且为非负值。由于内层函数是凸的，因此将通过卡罗需-库恩-塔克(Karush-Kuhn-Tucker，KKT)条件获取最优解。为了表示更加直观，将上、下行传输速率表示为

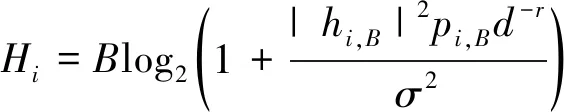
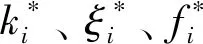
(10)

(11)

(12)

为了优化外层函数，在已知内层函数最优解的基础上通过梯度法对拉格朗日乘子进行优化，其中拉格朗日乘子表示如下：

(13)

(14)

(15)

其中，∂1、 ∂2、 ∂3为迭代步长，t为迭代次数且t≥0。

2.2 纳什均衡的存在性

为了证明博弈模型G存在一个纯策略纳什均衡，本文引入势博弈的概念。

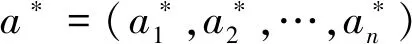
(16)

定义2如果存在一个势函数φ(a)对于任何一个终端设备i在i∈Lai,ai′∈Ai条件下使得下式成立：

Wi(ai,a-i)-Wi(ai′,a-i)

=φ(ai,a-i)-φ(ai′,a-i) (17)

则该博弈为完全势博弈。由于普通势博弈包含完全势博弈，因此完全势博弈具有普通势博弈的所有属性。

定理1如果一个普通势博弈具有有限的策略集合，那么它存在一个纯策略的纳什均衡。

定理2如果一个博弈模型是完全势博弈且存在势函数，那么存在一个纯策略的纳什均衡且具有有限递增属性。

证明首先设置势函数为

(18)

随后设置2个不同策略a=(ai,a-i)，a′=(ai′,a-i)并将2个不同的策略带入函数φ(a)与wi(ai,a-i)中得到：

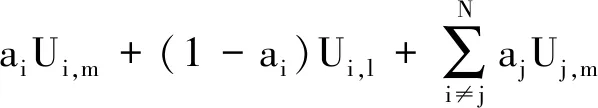
+(1-aj)Uj,l

(19)

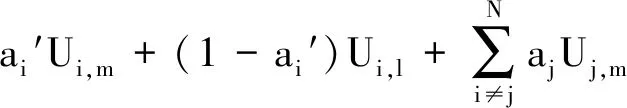
+(1-aj)Uj,l

(20)

Wi(a)=aiUi,m+(1-ai)Ui,l

(21)

(22)

基于式(19)～(22)可以得到：

φ(a)-φ(a′)=Wi(a)-Wi(a′)

(23)

因此上述博弈模型为完全势博弈且存在纯策略纳什均衡。

2.3 算法描述

由于边缘服务器拥有所有接入终端的完整信息，因此服务器可以根据接入信息获取优化后的卸载策略并将该策略发送至移动终端。根据纳什均衡性，所有移动终端将会服从该卸载决策。详细的算法描述如算法1所示。

算法1 基于博弈论的计算卸载与资源分配算法步骤 1 初始化:对终端卸载策略a,终端发射功率pi,B, pB,任务的输入数据大小si、输出数据大小mi以及任务所需的计算资源ci进行初始化;步骤2 在已知卸载策略基础上,获取任务卸载至本地终端时所需的执行时延Ui,l;步骤3 对于卸载至云端的任务通过式(10)～(12)获取上、下行资源以及计算资源的最优解k∗i、ξ∗i、 f∗i;步骤4 在步骤3的最优解基础上,通过式(13)～(15)对拉格朗日乘子进行更新;步骤5 基于步骤3和4,将卸载至服务端的任务时延Ui,m并与卸载至本地的任务时延Ui,l进行比较。如果Ui,m>Ui,l,则终端卸载至本地即ai=0否则ai=1。通过循环获取新的计算卸载策略a;步骤6 在已知策略a的基础上,设定其他终端卸载策略不变,单一改变终端i的卸载策略即ai=1,然后通过步骤3、4获取终端的任务时延。此时,如果Ui,l>Ui,m,ai=1同时对策略a进行更新。然后i+1且ai=1,重复步骤6直到终端i等于N时循环结束。此时得到最优的卸载策略a以及资源分配k∗i、 ξ∗i、 f∗i。

3 仿真结果与分析

为了验证本文所提基于博弈论的计算卸载与资源分配算法(CORAG)性能，在信道条件不变的基础上，分别与文献[21]所提的本地卸载算法(LOC)、随机卸载算法(random offloading completely, ROC)以及文献[19]提出的计算卸载与上行频谱资源分配(computation offloading and uplink resource game，COURG)进行比较分析。

3.1 参数设置

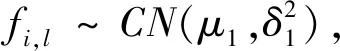
表1 仿真参数设置

3.2 仿真分析

首先考虑移动终端个数变化对系统总时延的影响。当终端的发射功率为23 dBm，边缘服务器的计算能力为30 000 Megacycles/s，上下行链路带宽相同且为20 MHz时，仿真结果如图2所示。图2表明，本文提出的CORAG算法的性能优于LOC、ROC以及COURG算法，随着移动终端数量增加CORAG算法优势更加明显。这是因为在计算与通信资源有限的条件下，CORAG算法可以更好地为不同的移动终端分配最优的计算与通信资源，因此所有移动终端的总时延最低。另外从图2可以看出，当所有移动设备的计算任务在本地执行时，由于计算任务时延的大小只与自身计算能力有关，因此随着终端数的增加，LOC算法的总时延是线性递增的；当采用随机卸载策略时，由于一部分移动终端会将任务卸载至边缘服务器而另一部分移动终端在本地执行计算任务，因此所有移动终端总时延低于LOC算法且呈波动变化。此外，由于COURG算法忽略了下行资源的优化，因此其总时延略高于CORAG算法。

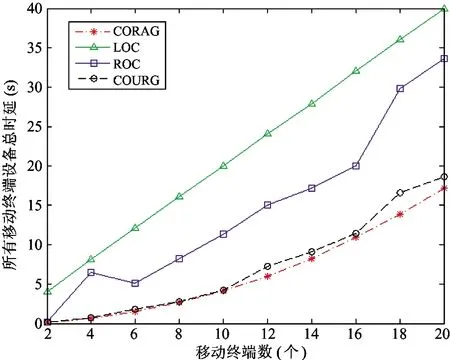
图2 不同算法在不同移动终端数量下的总时延比较

当移动终端数量为10、边缘服务器计算能力为30 000 Megacycles/s且上、下行带宽为20 MHz时，比较在不同输入数据大小下不同算法的性能，仿真结果如图3所示。由图3可以看出，随着上行输入数据的增大，CORAG算法总时延低于LOC、ROC以及COURG算法。这是因为CORAG算法可以根据获得输入数据的大小分配最优的上、下行带宽资源以及计算资源，进而使得所有终端设备的总时延最低。另外从图3明显看出，当计算任务在本地执行时，总时延仅与任务所需计算资源有关，因此LOC算法没有明显变化。

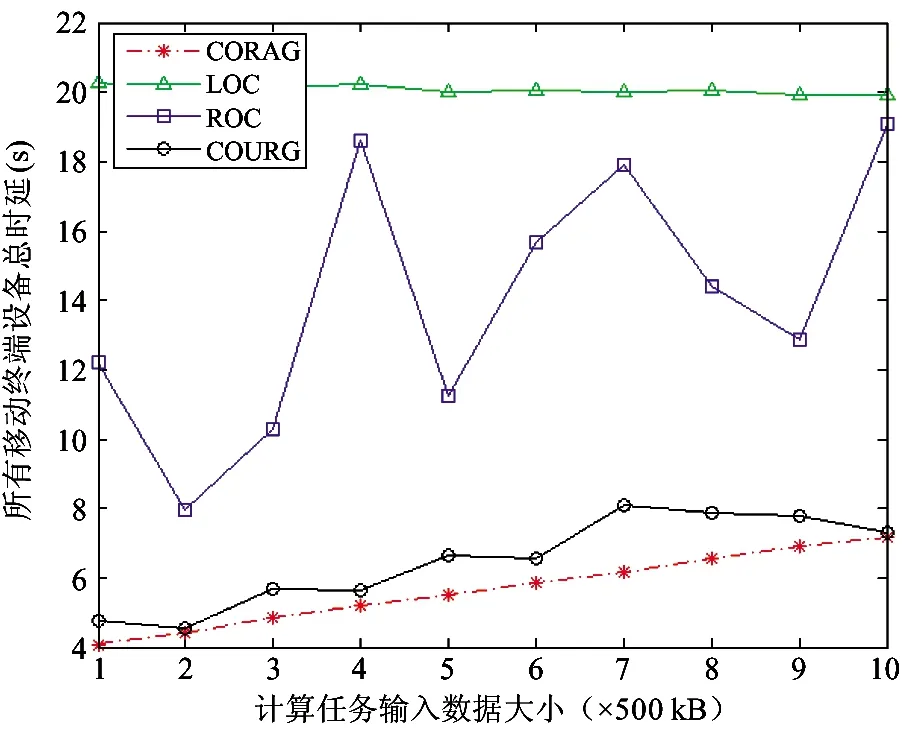
图3 不同算法在不同输入数据大小下的总时延比较

图4表示不同算法在不同计算结果数据大小下的性能仿真分析。仿真结果表明，随着计算结果数据的增大，CORAG算法的总时延低于LOC、ROC以及COURG算法。由图4可以看出，当计算结果大小不变时，所提算法性能明显优于其他3种算法且随着计算结果数据的逐渐增大，CORAG算法性能优势明显。此外，由于COURG算法忽略了下行带宽的优化，因此随着计算结果数据的增大，所有移动终端的总时延波动较大。而LOC算法的计算任务时延与计算结果大小无关，因此所有设备的总时延基本不变。最后，由于ROC算法中任务总是随机进行卸载，因此曲线是波动变化的。

图4 不同算法在不同计算结果数据大小下的总时延比较

为了进一步比较本文所提CORAG算法与LOC、ROC以及COURG 3种算法的性能，当移动终端数量为10、移动终端的计算能力为1 000 Megacycles/s且边缘服务器计算能力为35 000 Megacycles/s时，对不同算法在任务所需的CPU循环变化下进行仿真分析，仿真结果如图5所示。仿真结果表明，随着任务所需CPU循环的增加，消耗的资源逐渐递增。因此在资源有限条件下，4种算法的总时延逐渐上升。此外，由于CORAG与COURG算法对计算与通信资源进行了优化，因此算法性能优于LOC与ROC且上升趋势较为缓慢。另外从图5可以看出，随着任务所需CPU循环逐步增加，COURG算法曲线略微波动且在性能上与CORAG算法相近。这是因为随着任务所需CPU循环数的增加COURG算法总能为移动终端分配最优的计算资源，但由于该算法忽略了下行频谱资源的优化，因此COURG曲线会略微波动。

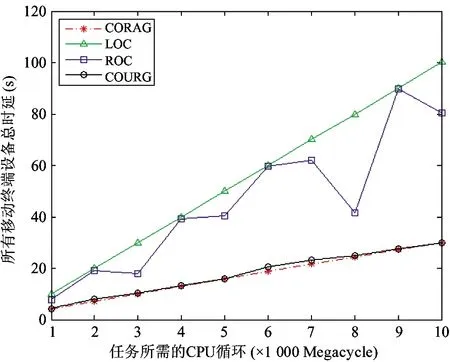
图5 不同算法在不同任务所需的CPU循环变化下总时延比较

最后，在不同边缘服务器的计算能力条件下对CORAG算法进行仿真，其仿真结果如图6所示。仿真结果表明，当移动终端数低于4时，边缘服务器计算能力大小对所有移动终端的总时延影响较小；当移动终端数从6逐步递增至20时，边缘服务器计算能力大小对所有移动终端的总时延影响较大。另外，通过对比计算能力为30 000 Megacycles/s与50 000 Megacycles/s曲线可知，当移动终端个数由14增长至20时，2条曲线总时延的差值也在逐步增大。

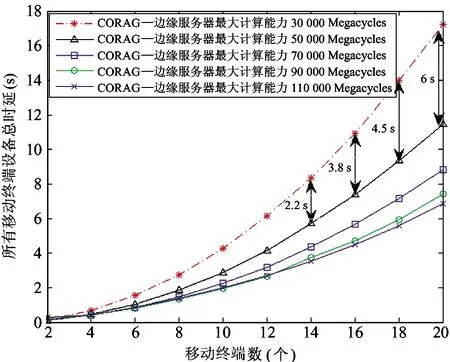
图6 随着移动终端数个数增加，不同边缘服务器计算能力条件下的CORAG算法性能比较

因此从以上结果可以得出，边缘服务器的计算能力越高，移动终端的时延越低。这是因为当终端个数较少时，现有的计算资源可以满足终端用户的需求；然而随着终端数量的增加其需要的计算资源将越来越多，此时服务器的计算资源越丰富，移动终端的总时延越低，算法的性能越优越。

4 结 论

本文针对计算能力不足的移动终端处理低时延、高可靠应用而产生高时延的问题，提出了一种基于博弈论的计算卸载与资源分配联合优化算法。该算法在设计过程中首先将计算卸载与资源分配问题表示为非合作博弈模型并通过引入势博弈概念证明该博弈模型存在纳什均衡状态；其次在已知移动终端卸载的决策条件下，利用拉格朗日乘子法获取计算资源以及上下行频谱资源的最优解；最后在最优解的基础上，采用迭代法获得移动终端的纳什均衡解。仿真结果表明，与LOC算法、ROC算法以及COURG算法相比，本文提出的CORAG算法可以降低所有移动终端的任务时延，提升终端用户的服务体验。本文主要研究是在单基站覆盖下多个移动终端在非合作场景中的时延优化问题。然而在实际应用场景中，移动终端是频繁移动的，而这将增加不同终端间的连接几率并使移动终端间的资源复用成为可能；此外由于网络具有不同的负载特性，如何根据不同网络特点进行有效的资源分配也是未来研究方向[22，23]。因此在终端频繁移动的条件下根据不同的网络特点，提出有效的资源分配算法降低终端任务时延是下一步的研究重点。