切换拓扑下多舞台移动机器人编队容错跟踪控制①

倪洪杰 朱俊威 俞 立 禹鑫燚

(浙江工业大学信息工程学院 杭州 310023)

0 引 言

随着现代展演艺术需求越来越旺盛，舞台演出中逐渐出现多个足形机器人、智能车台以及其他移动体等协同参与舞台演出，以提升演出效果[1, 2]。通常在各类实际演出中，多个舞台移动机器人往往需要根据演出剧情的特点进行编队移动演出，特别在现有演出中，经常要求多个相同控制结构的舞台移动机器人实现运动和状态表现一致性，以配合演员或者剧情变化来特定演绎。与多智能协同控制类似，多舞台移动机器人协同编队演出的核心问题同样是分布式协调控制，其目的是通过设计合适的控制协议，建立各舞台移动机器人之间的关系，实现共同的目标。同时多舞台移动机器人之间存在通讯拓扑连接，其拓扑可能随时间或任务目标的变化而进行实时切换。

在切换拓扑下的多智能体协同控制问题上，Shen等人[3]利用半马尔可夫链来描述可能由于网络通信复杂性而引起的随机拓扑交换，并提出了一种容错事件触发控制协议，以获得多智能体系统的领导跟随一致性。Saboori等人[4]研究了具有交换拓扑和有向通信网络图的线性时不变多智能体系统的协同执行器故障调节策略，故障可以同时发生在多个代理中。Gallehdari等人[5]研究了面向有向交换拓扑网络多智能体系统的分布式控制重构策略，将所提出的可重构控制律应用于一组自主水下航行器(ALIV)在有向切换拓扑和同时执行器故障等条件下的控制。Jia等人[6]讨论了在有向切换拓扑条件下四轴飞行器群的领导跟随问题，利用自适应神经网络状态观测器逼近未知非线性函数，重构不可测的内部状态，结合动态表面控制技术，提出了一种新的分布式输出反馈形成控制协议。Wang和Yang[7]研究一类高阶多智能体系统(MASs)的分布式容错控制问题，该系统具有切换无向拓扑、异构匹配不确定性、扰动和执行器失效、偏置、停机和阻塞等故障, 基于相邻节点的相关信息，通过分布式自适应机制，设计了一种新的容错一致性跟踪协议。Ye等人[8]研究了具有半马尔可夫跳变拓扑的复杂动态网络的容错同步控制问题,其主要目的是设计一个容错控制器，使闭环系统在执行机构发生随机故障时具有同步特性。Zheng和Zhang[9]利用增量算子方法研究了切换拓扑下多智能体系统故障和不匹配的一致性问题，引入了delta算子来统一连续、离散或采样系统在一个框架下的一致分析。Patel和Mehta[10]针对具有切换拓扑结构的离散多智能体系统，提出了一种领导跟随一致性的离散滑模协议。Yan等人[11]针对基于离散信息的开关通信拓扑结构下的多水下机器人协调控制问题，提出了具有或不具有时滞的协调控制协议。此外还有研究人员采用耗散理论和干扰观测的方法研究了具有静态领导者的多机器人系统跟踪控制问题[12]。

上述文献中大多只考虑了系统发生单个故障的情况，实际舞台移动机器人在演出过程中不可避免会因驱动执行器出现瞬间异常或者转速编码盘损坏等而出现各类故障现象，需要考虑在切换拓扑下的多移动机器人编队同步跟踪控制问题。本文和上述研究相比，主要突出点在于：(1)考虑了切换拓扑下的多舞台移动机器人跟踪控制问题，通过设计一种容错跟踪控制协议，在多个单体移动机器人均发生多种故障的情况也能保证群体同步运行。(2)观测器增益的切换并非随着拓扑实时变化。在切换拓扑后，计算拉普拉斯矩阵的特征值，只有当特征值上下界发生变化时，才需要重新计算观测器增益，从而避免了频繁切换增益。

1 问题描述

考虑实际演出中，有1+N个同构舞台移动机器人进行编队运动控制，其中由N个舞台移动机器人作为跟随机器人构建组成的一个网络，假设每一个跟随机器人的动力学方程可以用以下连续时间的线性时不变(linear time-invariant， LTI)系统来表示：

(1)

其中，xi(t)∈Rn,ui(t)∈Rm,yi(t)∈Rp分别表示跟随机器人的系统状态、控制输入和测量输出。fi(t),fsi(t)分别表示执行器故障、传感器故障，其导数范数均有界。wi(t)表示外部扰动，其范数有界。A,B,C,D,E,Bw为给定的实数矩阵。

1个同构舞台移动领航机器人的动力学方程为

(2)

其中，x0(t)∈Rn,r0(t)∈Rm,y0(t)∈RP分别表示领航机器人的系统状态、控制输入和测量输出，A、B、C同样为给定的实数矩阵。定义δi(t)=xi(t)-x0(t)作为第i个机器人节点的跟踪误差，由式(1)和(2)可以得到跟踪误差为

+Bwwi(t)

(3)

则可以得到一个增广后的误差跟踪系统：

(4)

其中i=1, 2, 3, 4。

2 主要结果

在设计切换拓扑下的容错跟踪控制协议前，先将扰动投影到匹配分量和不匹配分量[13]，如下所示：

(5)

(6)

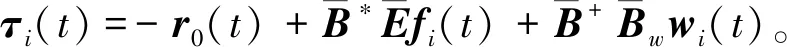
为构造分布式中间观测器，定义中间变量为

(7)

其中ω是一个调优参数。从式(6)和(7)中可以得到：

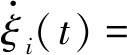
(8)

对于第i个机器人节点，基于式(6)、(8)，设计分布式中间观测器为

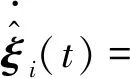
(9)

(10)

在前面分析的基础上，将第i个机器人节点的容错跟踪控制协议设计为

(11)

K的取值要使得A-BK是Hurwitz矩阵。将式(11)代入式(3)，得到第i个节点的闭环系统状态方程为

+Beξi(t)+Bw2wi(t)

(12)

由式(10)和(12)则整个闭环系统可以表示为

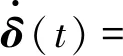
+(IN⊗S2)eξ(t)+(IN⊗Bw2)w(t)

(13)

其中，

M=L+G,S1=BK+ωBBT,S2=B

如果存在标量ω>0,ε>0，矩阵P1>0,P2>0,P3>0和H使得整个闭环系统的状态式(11)一致最终有界,则：

φi<0

(14)

其中，

证明给出Lyapunov函数为

V(t)=δT(t)(IN⊗P1)δ(t)

(15)

由式(13)和(14)，可以得到V(t)对时间的导数如下：

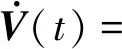
δT(t)[IN⊗P1(A-BK)+(A-BK)TP1]δ(t)

+2δT(t)(IN⊗P1S1)eδ(t)+2δT(t)(IN⊗P1S2)

(16)

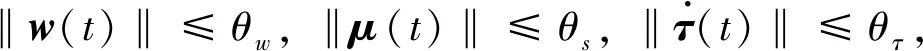
2δT(t)(IN⊗P1Bw2)w(t)

(17)

(18)

(19)

(20)

(21)

(22)

由式(15)～(22)得到：

+(A-BK)TP1]δ(t)

+2δT(t)(IN⊗P1S1)eδ(t)

+2δT(t)(IN⊗P1S2)

(23)

(24)

Σ11=He[IN⊗P1(A-BK)]

Σ12=IN⊗P1S1,Σ13=IN⊗P1S2,

+(1/ε)(IN⊗P3P3)

并且从式(15)中，可以得知:

V(t)≤max[λmax(P1),λmax(P2),λmax(P3)]

(25)

记Σp=-Σ，若Σ<0(即Σp>0)，则可以从式(24)和(25)中得出：

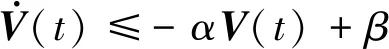
(26)

其中,

记集合Z为如下形式：

(27)

记Zs为Z的补集，则可以得知：

V(t)≥λmin(P1)‖δ(t)‖2

+λmin(P2)‖eδ(t)‖2

(28)

(29)

由于M是对称实矩阵，对M进行谱分解可以得到：

M=QΛQT

(30)

其中，Q是由M的特征值构成的矩阵，Λ= diag{λ1,…,λN} (i=1，2，…，N)是矩阵M的特征值。定义一个转移矩阵如下所示：

(31)

左乘Σ，右乘T及其转置后：

(32)

其中，

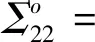
通过应用舒尔补引理，可得Σ<0，即Σo<0等价于式(14)。证毕。

注1本例所设计的切换拓扑下的多舞台移动机器人容错跟踪协议流程如图1所示，主要有以下步骤。

(1) 设定调优参数ω和反馈增益K，若最后估计性能不满意，则需要重新设定ω和K；

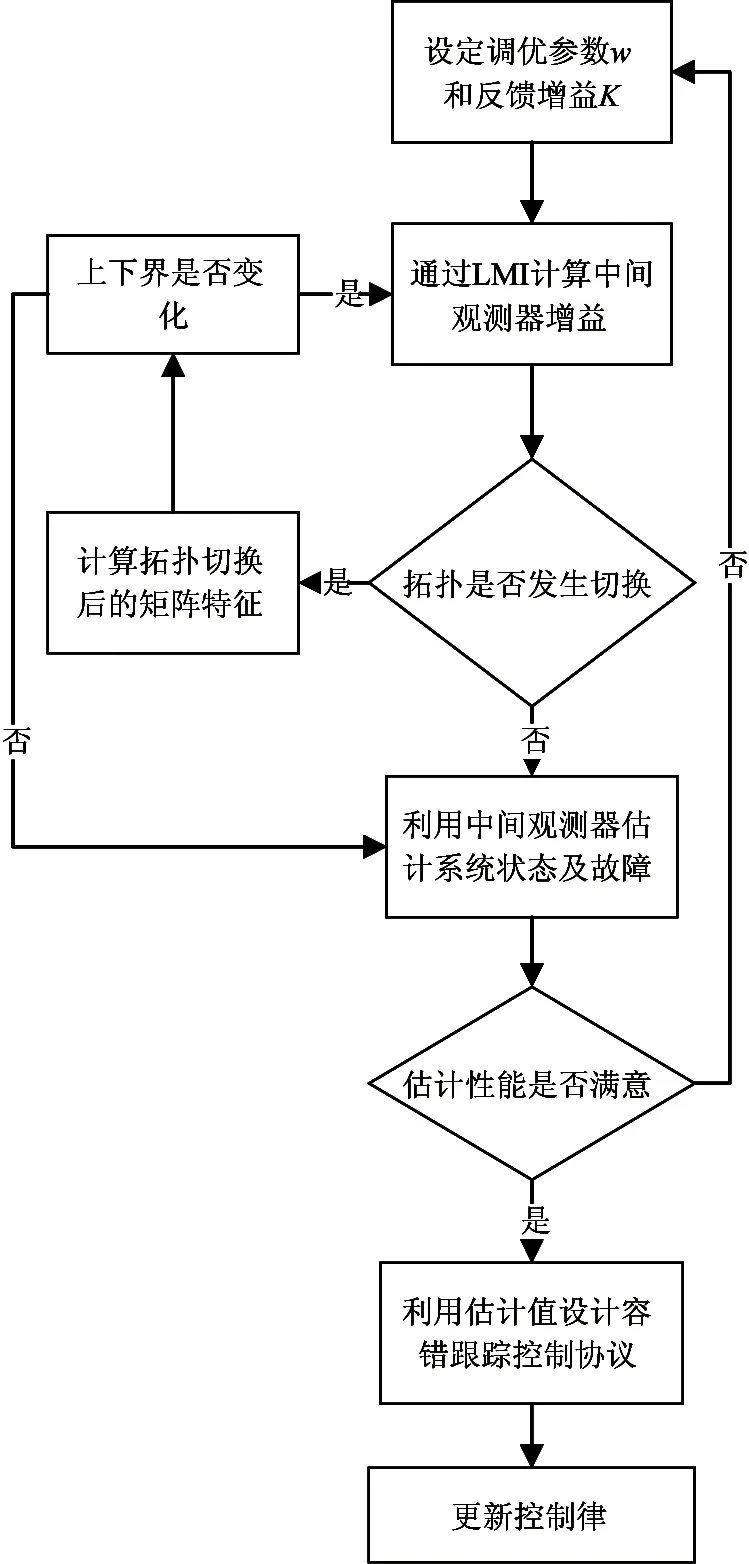
图1 容错跟踪控制协议流程图

(2) 在当前拓扑情况下，通过LMI计算观测器增益。由于本例中，系统之间的拓扑随时间而变化，因此需要根据当前拓扑的连接性质重新计算观测器增益；

(3) 设计中间观测器同时估计系统状态和发生的故障；

(4) 利用估计值设计基于状态反馈的容错跟踪控制协议，使得跟随机器人和领航机器人的状态保持一致。

注2在每次切换拓扑后，重新计算当前拓扑下拉普拉斯矩阵的特征值，由于最大最小特征值决定了式(12)是否有解，其本质上是一个凸条件。因此当特征值的上下界发生变化时，才需要重新计算观测器增益，避免了系统频繁切换。

3 仿真算例

由于舞台移动机器人运行在一个不完备的知识空间，因此需要为机器人编队设计一种实时检测故障，并保证编队同步运行的控制策略。本文以一种轮式移动机器人编队为例，通过仿真实验来说明所设计的容错跟踪控制协议的有效性。其中，舞台移动机器人的动力学模型[14]为

其中，Iv表示绕轮式机器人重心的转动惯量；m表示移动机器人总质量；l表示移动机器人宽度的一半；Iω表示移动机器人驱动轮的转动惯量；c表示车轮与地面的摩擦系数；r表示车轮半径；k表示移动机器人控制电机及驱动机构的驱动增益。

代入其具体参数：

Iv=10 kg·m2，m=50 kg，l=0.5 m,

Iω=0.05 kg·m2，c=0.05 kg·m2/s,

r=0.125 m，k=20 N·m/V

得到其领航机器人的状态空间方程为

考虑跟随机器人系统同时发生执行器故障和传感器故障以及扰动的情况，可得跟随机器人的状态空间方程：

假设外部扰动为wi(t)=0.1sin(0.2t)，u0(t)为控制输入。其中u0(t)的第1个分量表示右车轮的驱动电压ur(t)，u0(t)的第2个分量表示左车轮的驱动电压ul(t)，同前面领航机器人一样，任何跟随机器人无法直接获得该驱动实时量。同样假设u0(t)=r0(t)=3sin(0.2t)，需要指出的，在当前移动机器人系统框架下，故障fi(t)和fsi(t)实际上分别表示左车轮的驱动电压偏差和移动机器人方向角的量测偏差。在舞台表演中，移动机器人需要根据实际的表演需求不断变换其通讯拓扑，以满足各种各样的队形要求，图2为其拓扑变换流程。

图2 拓扑变换1流程图

为了模拟故障下同构移动机器人编队跟踪效果，设定各个跟随机器人的执行器和传感器故障，分别如表1和表2所示。

表1 执行器故障

表2 传感器故障

采用式(14)来计算观测器增益，由λ1、λ2、λ3特征值可以看出，在第2种拓扑情况下，4个特征值的上下界没有发生全部变化，因此在此拓扑情况下，不需要重新计算观测器增益，如图3所示。

在MatLab程序下进行本算法的仿真验证，领航机器人和跟随机器人的跟踪状态如图4、图 5所示，图6～9给出了组合未知信号及其估计值，图10给出了传感器故障及其估计值。从上述图表中可以看出，切换拓扑下的多舞台移动机器人容错跟踪控制问题得到了解决。

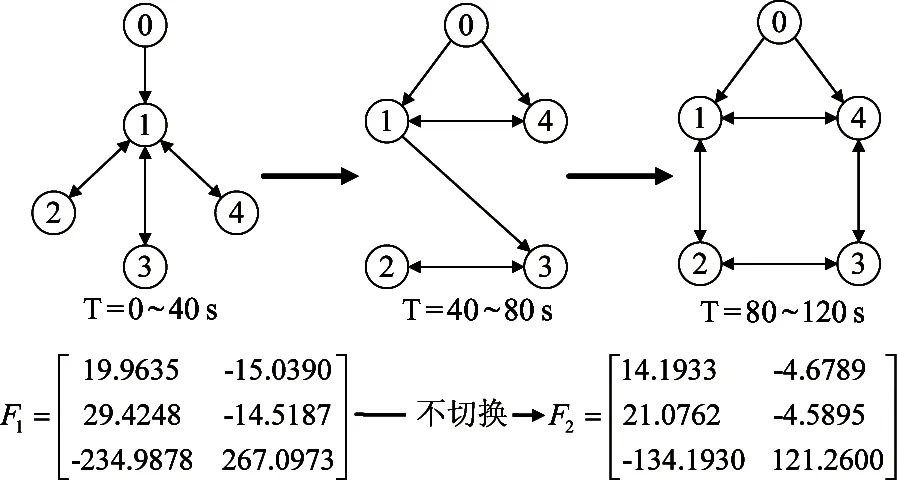
图3 拓扑变换2流程图

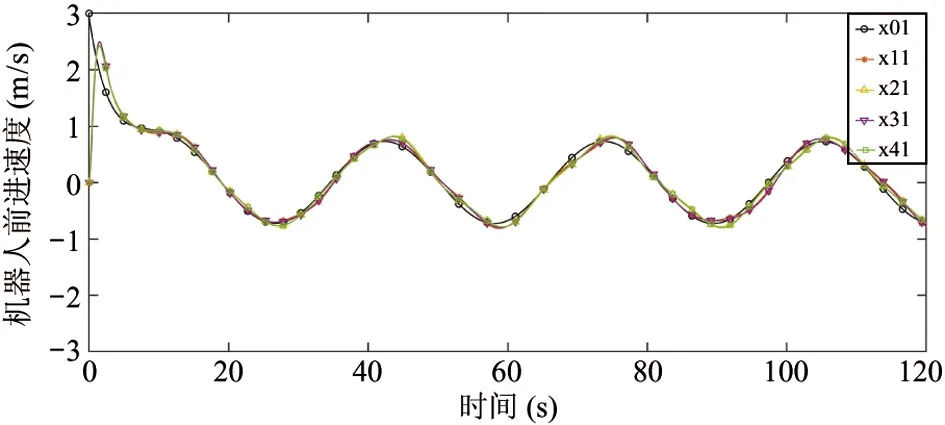
图4 领航与跟随机器人状态1

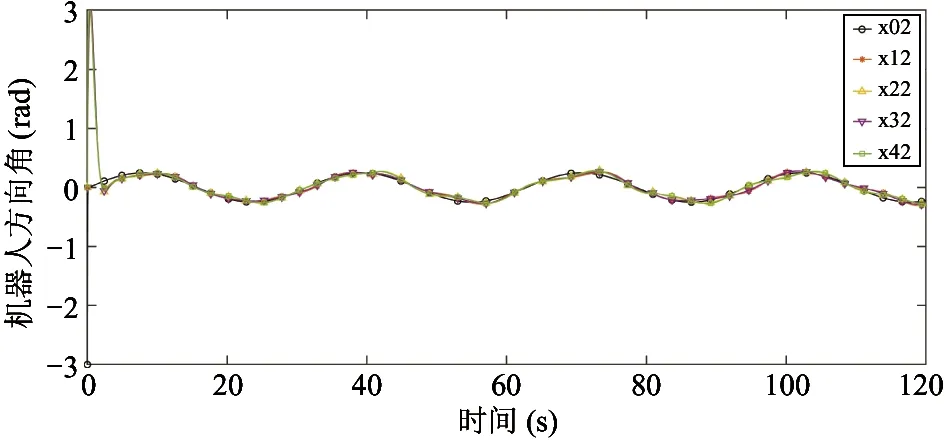
图5 领航与跟随机器人状态2

图6 组合未知信号1及其估计

注3本例中每个节点上有4个未知输入信号，但是每个节点只有2个输出，根据故障估计理论，无法单独估计每一个未知输入信号，因此本文将多个未知输入信号整合为一个组合未知信号进行估计，即τi(t)=-r0(t)+fi(t)+wi(t)。

注4本例中，在40 s和80 s分别切换一次拓扑，但观测器增益只切换了一次。从上述图表中可以看出，在增益切换时，系统状态和故障的估计均发生一定程度的抖动，但随后又立刻得到调节，并且其抖动的超调量较小，证明了本例中所设计的切换拓扑下的多舞台移动机器人容错跟踪控制协议的有效性。

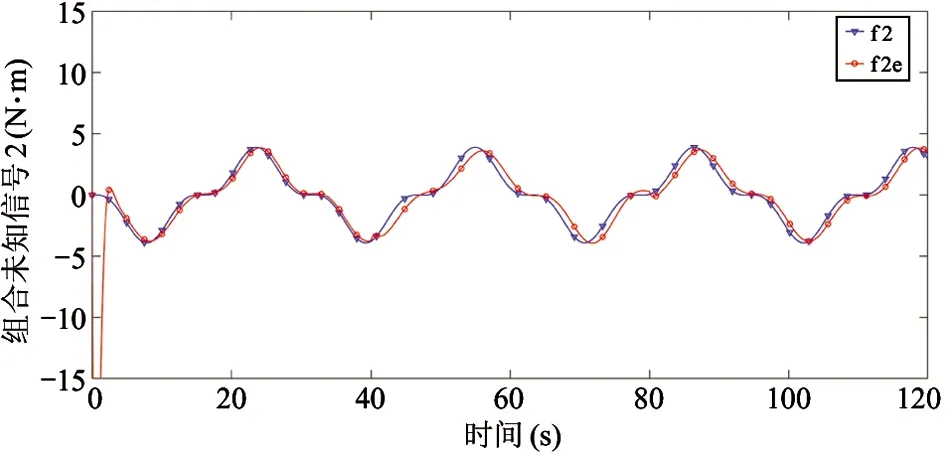
图7 组合未知信号2及其估计

图8 组合未知信号3及其估计

图9 组合未知信号4及其估计

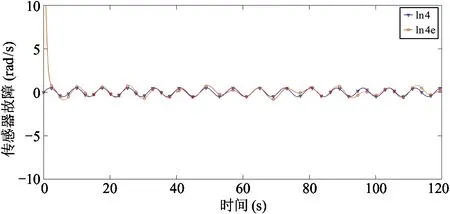
图10 传感器故障及其估计

4 结 论

围绕现代舞台演出高品质艺术表现需求，针对多舞台移动机器人协同编队演出特点，提出了一种在切换拓扑情况下的移动舞台机器人容错跟踪控制方法。在完成不确定性量进行匹配分量和不匹配分量分解后，继而通过分布式中间观测器设计来估计由多种组合未知输入信号，进而设计基于估计值的容错跟踪控制协议对匹配未知输入进行有效补偿，又通过调节特定参数充分抑制不匹配不确定性效应。机器人驱动器和传感器等多个故障发生下的仿真结果表明，本文设计方法仍能确保舞台移动机器人获得较好的容错跟踪控制性能，同时避免观测器增益频繁切换。下一步将围绕多舞台移动机器人故障特征点不确性来进一步提升容错控制算法的鲁棒性。