基于图像的VTOL飞行器视觉伺服控制①

邹立颖 刘真海 林钰川

(齐齐哈尔大学通信与电子工程学院 齐齐哈尔 161006)

0 引 言

近些年来，垂直起降(vertical take-off and landing ，VTOL)飞行器，由于具有对起降环境依赖小、机动性强等优点，被广泛应用于军事和民用等领域[1]。随着应用领域的不断扩大，VTOL飞行器的控制问题成为飞行器控制领域的研究热点[2]。VTOL飞行器是典型的欠驱动、非最小相位系统[3，4]，这给其控制研究带来了极大困难。目前为止，已有文献对其进行了深入研究[1-12]。文献[6]提出了一种非线性控制器，实现了全局渐进镇定控制。文献[7]采用模型分解的方法研究了输出轨迹跟踪问题。文献[8]采用观测器重构速度信号，实现了VTOL飞行器全局输出渐近跟踪。文献[9]应用饱和函数法进一步解决了输入受限情况下VTOL飞行器的轨迹跟踪问题。文献[11]基于最优控制提出了一种非线性状态反馈控制律，实现了VTOL飞行器的镇定控制。上述工作都没有考虑VTOL飞行器的定点降落问题。

本文对VTOL飞行器的定点降落问题展开研究。一般来说，VTOL飞行器的位置和姿态都是由全球定位系统(GPS)和惯性测量单元(IMU)获取[12]，但是GPS实时性差，IMU的精度低，对于定位精度高和实时性强的特殊任务(如定点降落)难以胜任。作为一种强大的感知环境的有效工具，视觉传感器具有精度高、实时性强等优点[13,14]，适合于执行特殊任务。近10年来，视觉伺服技术已经广泛地被应用于控制领域[15-20]，视觉伺服技术主要分为2类[15]，即基于位置的视觉伺服(position-based visual servo, PBVS)和基于图像的视觉伺服(image-based visual servo, IBVS)。PBVS需要精确的物体模型，且对图像误差及摄像机标定误差敏感。IBVS将误差直接定义在图像空间，对图像误差及摄像机标定误差不敏感。本文采用IBVS方法解决VTOL飞行器的定点降落问题。文献[21]于2008年提出了一种新的双目视觉伺服模型，由于该模型不需要未知点的深度信息，模型维度低，易于计算。因此本文采用该双目视觉模型。

对于VTOL飞行器的定点降落控制问题，本文提出了一种基于图像的视觉伺服控制方案。其主要贡献是将基于图像的视觉伺服控制方法推广到VTOL飞行器系统。利用机载摄像头获取图像信息，基于反步法设计了视觉伺服控制器，引导VTOL飞行器定点降落在期望位置。所采用的视觉模型中不包含深度信息，从而避免了未知点深度信息的测量或估计。利用李雅普诺夫理论证明了，在所提出控制器作用下VTOL飞行器闭环系统渐近稳定，图像误差最终收敛为0，实现了基于图像视觉伺服控制。

1 VTOL飞行器数学模型

通常讨论的VTOL飞行器动力学模型是由文献[5]提出的简化模型：

(1)

其中，(y,z)是VTOL飞行器质心的水平和垂直方向位置，φ为滚转角，u1和u2为飞行器底部推力控制输入和滚动控制输入，g为重力加速度，ε是描述滚动控制输入和横向加速度关系的耦合系数。

本文解决的是VTOL飞行器的定点降落问题，给定飞行器的目标降落位置Yd=(Y1d,Y2d)，控制目标为设计控制律使得VTOL飞行器系统平稳降落到目标位置。

对系统式(1)，采用输入变换：

(2)

其中，v1和v2为新的控制输入，则系统式(1)变为

(3)

(4)

整理得：

(5)

其中，

2 双目视觉模型

根据文献[20]，双目视觉模型为

(6)

(7)

式中，Ji(mi)∈R3×6表示特征点mi的图像雅可比矩阵。

该视觉模型不包含深度信息，避免了深度信息的测量与估计。

由于摄像机安装在飞机质心位置，则有：

(8)

其中，

进而得：

(9)

式中，K(mi)=Ji(mi)A

3 视觉伺服系统控制器设计

为了实现定点降落的控制目标，本文利用机载摄像头获取目标物体的图像信息，采用基于图像的视觉伺服控制方法，同时结合反步法设计出视觉伺服控制器，引导飞行器系统自主降落在目标位置。

为了便于研究，取目标上一个特征点进行研究，令目标点的图像特征m=y1，w=y2，由式(5)和式(9)得VTOL飞行器视觉伺服系统：

(10)

令目标点的期望图像特征md=y1d，并定义视觉伺服系统的图像误差：

e1=y1d-y1

(11)

(12)

定义Lyapunov函数：

(13)

对上式求导，并将式(12)代入可得：

(14)

基于反步法，选取虚拟控制量：

y2d=K+(y1)Λe1

(15)

其中，K+(y1)为K(y1)的伪逆矩阵，Λ为待设计的正定矩阵。

定义误差变量：

e2=y2d-y2

(16)

将式(15)和(16)代入式(14)可得：

(17)

为了保证系统的稳定性，将滑模面设计为

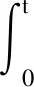
(18)

其中，K1为待设计的正定矩阵。

定义Lyapunov函数：

(19)

对上式求导得：

(20)

设计滑模控制律为

(21)

其中，M为待设计的正定对角矩阵。

将式(21)代入式(20)得：

下面以定理1形式给出本文主要成果。

定理1对于VTOL飞行器视觉伺服系统式(10)，如果采用式(21)控制器，则闭环系统是渐近稳定的，即m→md,w→0。

4 仿真结果

仿真结果如下。

图1为特征点在左右摄像机图像平面的轨迹曲线，圆圈为初始点位置，星号为期望点位置，由图可见，特征点由初始点顺利到达期望点。图2表示图像误差曲线，可以看出，图像误差快速收敛为0，收敛精度高。图3表示飞行器滚转角及其角速度变化曲线，图3表明滚转角及其角速度收敛速度快，稳定性好。图4和图5分别表示飞行器的水平和垂直方向位置和速度收敛曲线，由图4和图5可以看出，飞行器的位置和速度收敛速度快，在10 s内完成收敛，动态过程平稳。图6为VTOL飞行器控制输入曲线，可以看出控制器响应迅速、稳定收敛。仿真结果表明VTOL飞行器能够快速、准确地到达目标位置，同时保证滚转角及其角速度渐近收敛到0，系统内部动态稳定，本文设计的控制器效果良好。

图1 特征点在左右摄像机图像平面轨迹

图2 图像误差曲线

图3 滚转角及滚转角速度

图4 水平位置和速度曲线

图5 垂直位置和速度曲线

图6 控制输入

5 结 论

本文提出一种基于图像视觉伺服技术与反步控制方法相结合的控制策略，将基于图像的视觉伺服控制方法应用到VTOL飞行器系统。将反步法与滑模控制技术相结合设计了视觉伺服控制器，解决了飞行器自主定点降落控制问题。该方法所采用视觉模型不含深度信息，直接利用图像信息即可获得图像雅克比矩阵，无需测量或估计未知点的深度信息，因而提高了系统的控制性能。利用李雅普诺夫理论给出了闭环系统的稳定性证明。仿真结果表明，所提出的方法能够保证VTOL视觉伺服系统快速、稳定地到达期望目标位置，图像误差渐近收敛为0，实现了基于图像的视觉伺服控制。