基于(N, T)休眠机制的云计算中心节能策略及优化①
王晓琛 王宇廷 张丽媛 金顺福
(*燕山大学信息科学与工程学院 秦皇岛 066004) (**河北省计算机虚拟技术与系统集成重点实验室 秦皇岛 066004) (***廊坊师范学院理学院 廊坊 065000)
0 引 言
随着云计算应用的普及与云服务规模的扩大,云数据中心在面向各界提供高性能服务的同时,产生了巨大的能量消耗[1,2]。如何在保证云系统节能效果的前提下,提高云用户请求响应性能成为相关领域的研究热点。
针对云计算数据中心的高能耗问题,部分学者使用虚拟机整合技术对节能策略进行了相关研究。Fayyaz等人[3]为了降低云数据中心的总体能耗,提出基于虚拟机/任务整合的云基础架构,通过虚拟机监视器将任务从未充分利用的服务器迁移到合适的服务器,使用动态阈值电压调节算法关闭空闲服务器。Zhou等人[4]提出一种虚拟机整合算法,针对不同类型的主机,进行基于主机负载预测的虚拟机迁移,研究云数据中心的空闲能耗问题。Tang等人[5]为了降低云数据中心服务器、通讯网络及冷却系统的总体能耗,提出基于工作负载预测的节能作业调度算法,使用虚拟机迁移及整合技术,关闭相应模块及机架。
还有部分学者基于休眠模式研究了云数据中心的节能问题。Fan等人[6]为了降低云数据中心的总体能耗,提出基于多种休眠模式的服务器调度方案。使用绿色休眠管理器制定服务器活跃模式及多睡眠模式的时间表,确保有足够的服务器以最低的能耗为云请求提供服务。Jin等人[7]为了提高云数据中心的能源效率,提出具有速度切换及多重休眠模式的节能策略。基于当前的工作负载,确定主虚拟机的运行速度及备用虚拟机的状态。为了实现系统节能,Hou等人[8]提出基于多种休眠模式的嵌入式系统的节能优化算法。在估计空闲持续时间长度之后,制定最优控制算法选择合适的休眠模式。在上述文献的休眠模式中,只有休眠定时器超时,系统才能从休眠期切换至唤醒期,而不考虑系统中的云用户请求数量,在一定程度上影响了云用户请求的响应性能。
本文兼顾云数据中心的能量效率与云用户请求的响应性能,面向多虚拟机引入(N,T)休眠机制,研究了云系统的节能策略与优化问题。
1 能量节省策略及系统模型
1.1 能量节省策略
在传统的云数据中心中,除了处理云用户请求需产生的必要能耗外,云系统在空闲时也会产生额外的能耗,造成能源浪费。为了在保证云用户服务质量的前提下,最大限度地提高云数据中心的能量效率,本文面向多虚拟机提出一种带有(N,T)休眠机制的节能策略。该策略的工作原理如图1所示。
当云系统中全部云用户请求都完成服务,即云系统变空时,全部虚拟机同时进入休眠状态,云系统由唤醒状态进入节能状态。云系统节能状态内第一个到达的云用户请求使虚拟机由休眠状态转入休眠监听状态,并启动一个长度为T的计时器及阈值为N的计数器。计时器及计数器中的任何一个失效,都将同时唤醒全部的虚拟机,即全部虚拟机同时进入运行或空闲状态,云系统将从节能状态切换至唤醒状态。
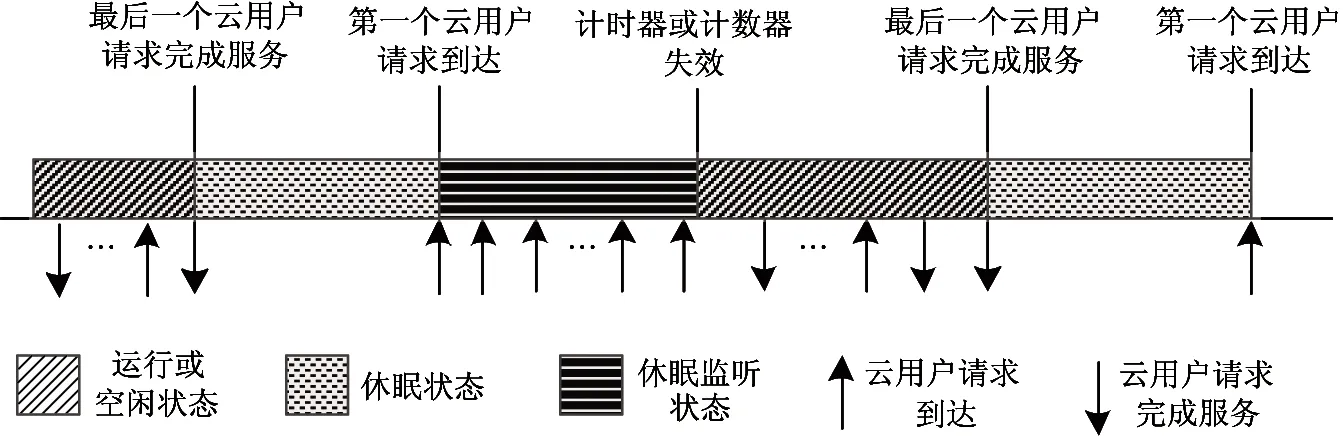
图1 (N, T)休眠机制的工作原理
1.2 系统模型
将云用户请求抽象为顾客,将虚拟机抽象为服务台,将休眠状态抽象为休假,基于(N,T)休眠机制可建立多重同步休假随机模型。
假设所有云用户请求是同质的,所有虚拟机是同构的。云用户请求到达间隔服从参数为λ(λ>0)的指数分布,服务一个云用户请求的时间服从参数为μ(μ>0)的指数分布,休眠定时器的长度T服从参数为θ(θ>0)的指数分布。
令随机变量L(t)表示t时刻系统中云用户请求的数量,称为系统水平。令随机变量J(t)表示云系统所处的状态。J(t)=0表示云系统处于节能状态,虚拟机或者休眠或者休眠监听。J(t)=1表示云系统处于唤醒状态,虚拟机或者空闲或者运行。{(L(t),J(t)),t≥0}构成一个2维连续时间马尔可夫链,其状态空间Ω表示为
Ω={(i,j)|i=0,1,2,…,j=0,1}
(1)
令πi, j表示稳态下云系统水平为i且云系统处于状态j的概率分布,则有:
i=0,1,2,…,j=0,1 (2)
令πi(i≥0)表示稳态下云系统水平为i的概率向量,πi=(πi0,πi1,πi2,…)。则该马尔可夫链的稳态概率分布π由πi(i≥0)构成,π表示为π=(π0,π1,π2,…)。
2 模型分析和性能指标
2.1 模型分析
令Q表示连续时间马尔可夫链{(L(t),J(t)),t≥0}的一步状态转移率矩阵,Qx, y表示系统从x(x=0,1,2,…)水平跳转至y(y=0,1,2,…)水平的转移率子阵。在第2节给出的假设条件下,马尔可夫链中L(t)的跳转只能发生在相邻水平之间。为表示方便,用Bx代替系统水平下降的子阵Qx,x-1,用Ax代替系统水平不变的子阵Qx,x,用Cx代替系统水平上升的子阵Qx,x+1。
在多重同步休眠机制中,只有在虚拟机处于休眠状态时到达一个云用户请求后,才启动阈值为N的计数器,故设置唤醒阈值下限Nmin=2个;为了保证所有的云用户请求都能在虚拟机唤醒以后立即被服务,故设置唤醒阈值上限Nmax=c个。
考虑到唤醒阈值N不大于系统中的虚拟机数量c,分Bx、Ax及Cx,并给出一步状态转移率矩阵Q。
首先,根据跳转前不同的系统水平讨论一步状态转移率子阵Bx。
跳转前系统水平x=0时,全部虚拟机处于休眠状态,不存在一步状态转移率子阵B0。
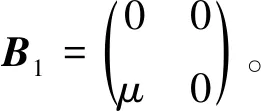
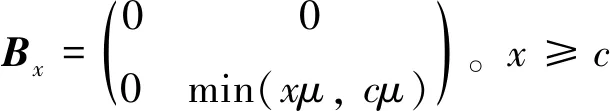
其次,根据跳转前不同的系统水平讨论一步状态转移率子阵Ax。
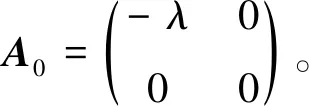
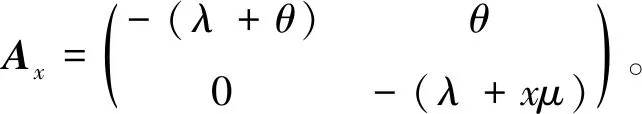
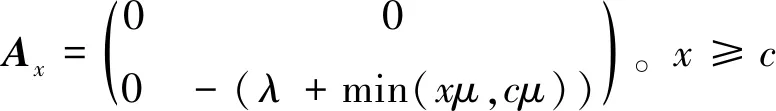
最后,根据跳转前不同的系统水平讨论一步状态转移率子阵Cx。

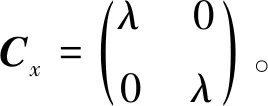
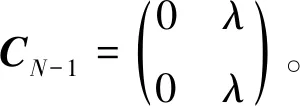
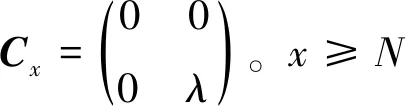
按照系统水平从低到高的顺序,系统一步状态转移率矩阵Q写为
Q=
(3)
由一步状态转移率子阵Q的结构可知,马尔可夫链{(L(t),J(t)),t≥0}是一种拟生灭过程,该过程正常返的充分必要条件是矩阵二次方程R2B+RA+C=0的最小非负解R(称为率阵R)的谱半径SP(R)<1。
转移率子阵A,B及C都是右下角只有一个非零元素的方阵,因此,率阵R也必然有相同的结构。设
(4)
其中,r22是实数。
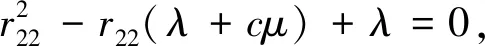
构造方阵B[R]如下:
B[R]=
(5)
基于平衡方程及正规化条件,建立方程组:
(6)
其中,e是维数为2×c的全1列向量,e1是维数为2的全1列向量。
利用高斯-赛德尔法[9](Gauss-Seidel method)求解方程组式(6),可得πi(i=0,1,…,c)的数值解。结合矩阵几何解方法,给出πi=πcRi-c,i>c,可进一步求得πi(i=c+1,c+2,…)的数值解。
2.2 性能指标
云用户请求响应时间定义为从云用户请求到达云系统开始到服务完成为止的时间长度[10]。一个云用户请求响应时间包含在系统缓冲区中的等待时间及在虚拟机上的服务时间。运用Little公式[11],云用户请求平均响应时间D的表达式为
(7)
云系统节能水平定义为单位时间内云系统因休眠机制的引入而减少的能量消耗。云系统处于唤醒状态时消耗正常的能量,处于节能状态时节省能耗;由节能状态切换至唤醒状态的过程会增加额外的能耗。云系统节能水平S的表达式如下:
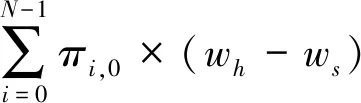
(8)
其中,wh表示云系统处于唤醒状态时单位时间内的能量消耗,ws表示云系统处于节能状态时单位时间内的能量消耗,wa表示云系统由节能状态切换至唤醒状态的能量消耗。
3 系统实验
为了在不同服务率μ下进一步研究唤醒阈值N及休眠参数θ对虚拟机调度策略的影响,进行数值实验及仿真实验。数值实验基于式(7)和式(8)用Matlab R2016a进行;仿真实验基于(N,T)休眠机制采用Java语言在MyEclipse2014下进行。
图2刻画了不同唤醒阈值N及服务率μ下云用户请求平均响应时间D随休眠参数θ的变化趋势。
由图2可知,若服务率μ及唤醒阈值N固定,随着休眠参数θ的增大,云用户请求平均响应时间D整体呈下降趋势。休眠参数越大,休眠定时器长度越短,云用户请求在系统节能状态的滞留时间越少,因而,云用户请求平均响应时间减小。特别地,当休眠参数θ=0.0时,系统退化为纯N策略,云用户请求平均响应时间较长;当唤醒阈值N=∞时,系统退化为纯T策略,云用户请求平均响应时间也较长。与传统的纯N策略及纯T策略相比,(N,T)策略下的云系统休眠机制改善了云系统的响应性能。
从图2可以看出,当μ=1.3,θ<4.0时,云用户请求平均响应时间D随着唤醒阈值N的增大呈现出增加的趋势;当μ=1.3,θ>4.0时,唤醒阈值N对云用户请求平均响应时间D无影响。

图2 休眠参数对云用户请求平均响应时间的影响
为了准确了解唤醒阈值N对云用户请求平均响应时间D的影响,图3刻画了不同休眠参数θ及服务率μ下云用户请求平均响应时间D随唤醒阈值N的变化趋势。
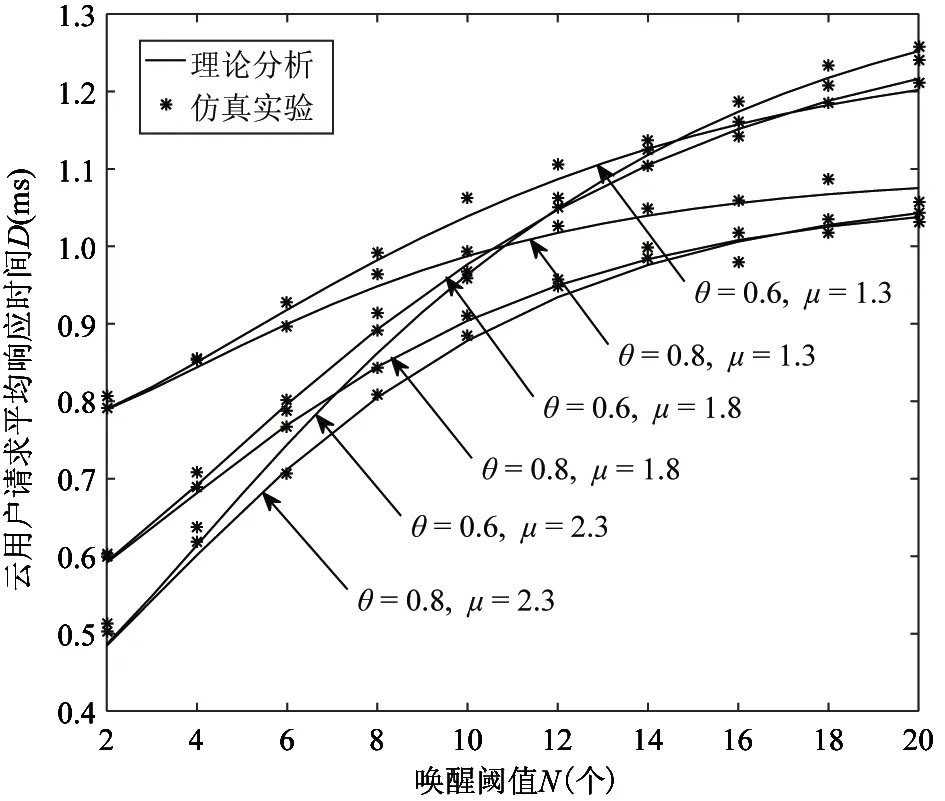
图3 唤醒阈值对云用户请求平均响应时间的影响
由图3可知,若服务率μ及休眠参数θ固定,随着唤醒阈值N的增大,云用户请求平均响应时间D整体呈增加趋势。唤醒阈值越大,节能状态下云用户请求数达到唤醒阈值所需的时间越长,因而云用户请求平均响应时间增加。
图4刻画了不同唤醒阈值N及服务率μ下云系统节能水平S随休眠参数θ的变化趋势。

图4 休眠参数对云系统节能水平的影响
由图4可知,若服务率μ及唤醒阈值N固定,随着休眠参数θ的增大,云系统节能水平S整体呈下降趋势。休眠参数越大,休眠定时器长度越短,云用户请求在系统节能状态的滞留时间越少。由于云系统处于节能状态时单位时间内的能量消耗低于系统唤醒状态时的能量消耗,因而,云系统节能水平降低。特别地,当休眠参数θ=0.0时,系统退化为纯N策略,云系统节能水平较高;当唤醒阈值N=∞时,系统退化为纯T策略,云系统节能水平也较高。(N,T)策略下云系统休眠机制响应性能的改善是以牺牲一定的云系统节能水平为代价的。
图4可以看出,当μ=1.3,θ<3.0时,云系统节能水平S随着唤醒阈值N的增大呈现出增加的趋势;当μ=1.3,θ>3.0时,唤醒阈值N对云系统节能水平S无影响。
为了准确了解唤醒阈值N对云系统节能水平S的影响,图5刻画了不同休眠参数θ及服务率μ下云系统节能水平S随唤醒阈值N的变化趋势。
由图5可知,若服务率μ及休眠参数θ固定,随着唤醒阈值N的增大,云系统节能水平S整体呈增加的趋势。唤醒阈值越大,系统节能状态内云用户请求数达到唤醒阈值所需的时间越长,即系统处于节能状态的时间越长,因而,云系统节能水平提高。
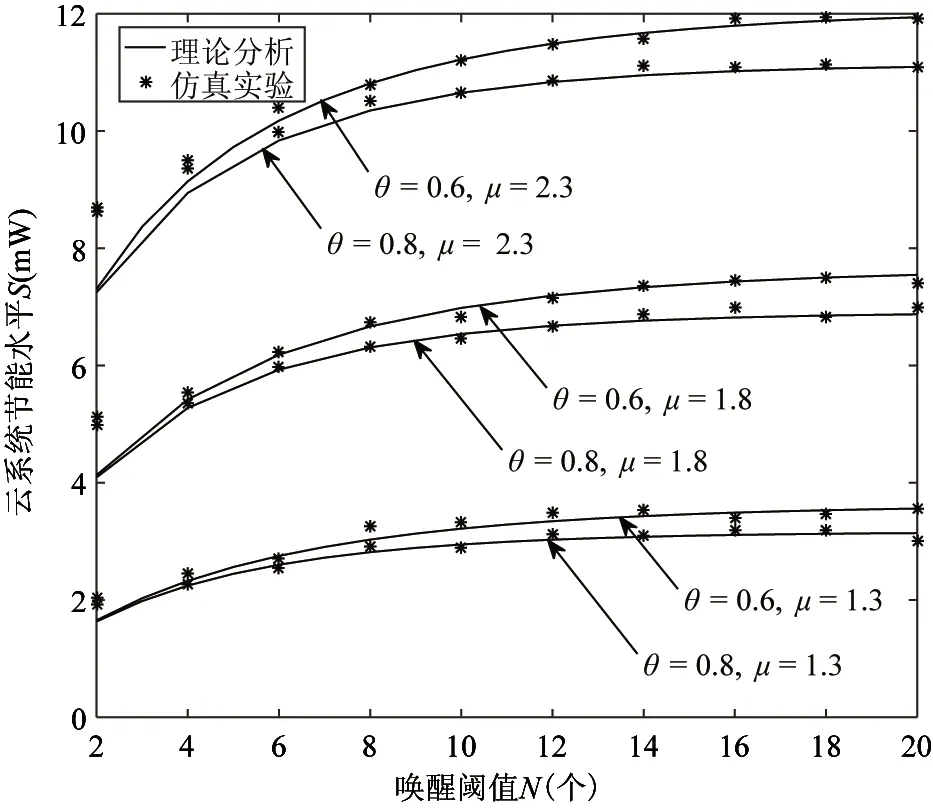
图5 唤醒阈值对云系统节能水平的影响
综合图2和图3揭示出的云用户请求平均响应时间的变化趋势与图4和图5揭示出的云系统节能水平的变化趋势,可以看出在设置休眠参数θ及唤醒阈值N时,云用户响应性能及云系统节能效果之间存在折衷关系。过大的休眠参数θ可以降低云用户响应时间,但降低了云系统节能水平。过大的N可以提高云系统节能水平,但又影响了云用户响应性能。为此,面向(N,T)休眠机制的虚拟机节能策略,需要联合优化休眠参数θ及唤醒阈值N。
4 系统优化
为了寻找云用户响应时间D及云系统节能水平S之间的平衡点,需要联合优化休眠参数θ及唤醒阈值N。
由图2~图5的实验结果,给出不同服务率μ下云用户请求平均响应时间的最大值Dmax及云系统节能水平最大值Smax。无量纲化云用户请求平均响应时间与云系统节能水平,采用权重算法[12],建立系统成本函数H为
(9)
其中,f1与f2表示权重系数,且f1+f2=1。
由2.2节的理论分析可知,云用户请求平均响应时间D与云系统节能水平S均很难用休眠参数θ与唤醒阈值N显示表示,系统成本函数H的封闭解也很难求出。因此,利用传统的理论分析方法难以给出系统成本函数H的优化结果。
群体智能优化算法具有操作简单、不受目标函数形式影响的特点,但容易陷入局部最优。本文以提高全局搜索能力为目的,综合使用对数螺旋函数及正弦函数更新飞蛾的当前位置,改进飞蛾扑火优化(moth-flame optimization, MFO)算法[13],用于优化(N,T)休眠机制的系统参数。该算法的主要步骤如算法1所示。

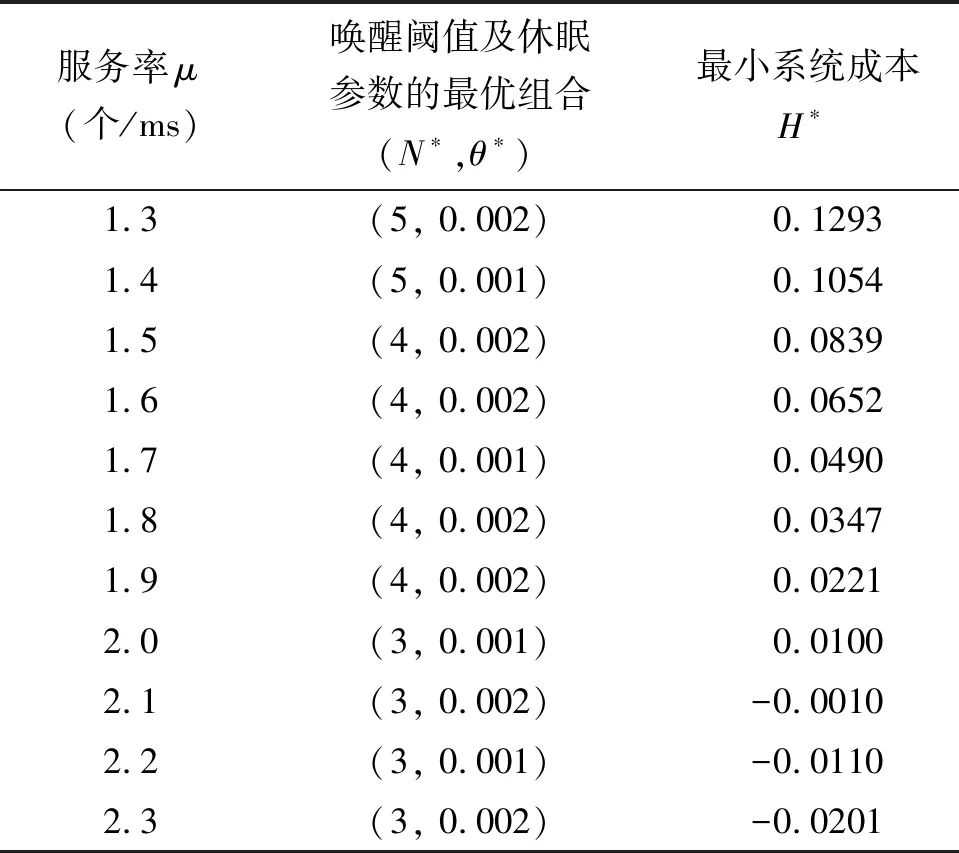
算法1 (N, T)休眠机制系统参数的优化算法Input: 种群数量n,最大迭代次数Imax,唤醒阈值下限Nmin及上限Nmax,休眠参数下限θmin及上限θmaxOutput: 最小成本H∗,最优参数组合(N∗,θ∗)1: for N=Nmin:Nmax2: 构建n×3二维表M3: M(i,1)=N, i∈{1,2,…,n}4: M(i,2)=rand·(θmax-θmin)+θmin, i∈{1,2,…,n} % 初始化休眠参数5: M(i,3)=H(M(i,1),M(i,2)), i∈{1,2,…,n} % 由式(4)计算系统成本函数6: 创建与表M内容相同的表F,并对表F按最后一列值升序排序,构造表X存放表F第一行的内容7: Iter=18: f=roundn-IterImax(n-1)()9: for Iter=2:Imax10: M(i,1)=N, i∈{1,2,…,n}11: t=-2+IterImax()·rand+1 % t为[-2,1]之间的随机数12: Di=|(M(i,1), M(i,2))-(F(i,1), F(i,2))|, i∈{1,2,…, f} % 计算表M中前f个系统参数与表F中前f个系统参数之间的欧氏距离13: M(i,2)=Di·ebt·sin(2πt)+F(i,2),i∈{1,2,…, f} % 利用螺旋函数及正弦函数更新表M中前f个休眠参数14: Di=|(M(i,1), M(i,1))-(F(f,1), F(f,2))|,i∈{f+1,…,n} % 计算表M中后(n-f)个系统参数与表F中最后一行系统参数之间的欧氏距离15: M(i,2)=Di·ebt·sin(2πt)+F(f, 2), i∈{f+1,…,n} % 利用螺旋函数及正弦函数更新表M中后(n-f)个休眠参数16: M(i,3)=H(M(i,1), M(i,2)), i∈{1,2,…,n}17: 结合表M与表F,构造表R,并对表R按最后一列值升序排序18: f=roundn-IterImax(n-1)()19: 清空表F,抽取表R中前f行的内容,放入表F中20: endfor 21: if F(1,3) 利用改进的飞蛾扑火优化算法进行实验。实验过程中的休眠参数范围为[θmin,θmax]。考虑休眠定时器长度为无穷大,设置休眠参数下限为θmin=0.0 m/s。由图2与图4可知,当休眠参数θ>11.0 m/s时,随着休眠参数θ的增大,云用户请求平均响应时间及云系统节能水平的变化很小,因此,设置休眠参数上限为θmax=12.0 m/s。算法所需其他实验参数设置如表1所示。 表1 实验参数设置 将上述实验参数代入算法1给出的算法中,在不同服务率μ下寻找出最小系统成本H*,并给出唤醒阈值N及休眠参数θ的最优组合(N*,θ*)。系统优化数值结果如表2所示。 表2给出的系统优化数值结果是在表1所设权重系数下得到的。在实际应用中,对于实时性要求高的云系统,通常设置较大的权重系数f1,而对于追求高节能效果的云系统,则应设置较大的权重系数f2。 表2 系统优化数值结果 折衷考虑云数据中心的节能水平与云用户请求的响应性能,提出了基于(N,T)休眠机制的云计算中心节能策略。结合唤醒阈值及休眠定时器,建立了一种多重同步休假随机模型,并给出了2维马尔可夫链的一步状态转移率矩阵。利用矩阵几何解方法,给出了云系统节能水平与云用户请求平均响应时间等性能指标。在Matlab R2016a平台下基于性能指标的理论分析进行了数值实验,在Myeclipse2014平台下采用Java语言进行了仿真实验。实验结果表明,较大的休眠参数可以减少云用户响应时间,但降低了云系统节能水平;较大的唤醒阈值可以提高云系统节能水平,但又影响了云用户响应性能。权衡不同性能指标,建立系统成本函数,通过改进飞蛾扑火优化算法,给出了云数据中心节能策略的联合优化结果。 在下一步的工作中,将引入延迟休眠机制,进一步研究响应性能更高的云计算中心的节能策略。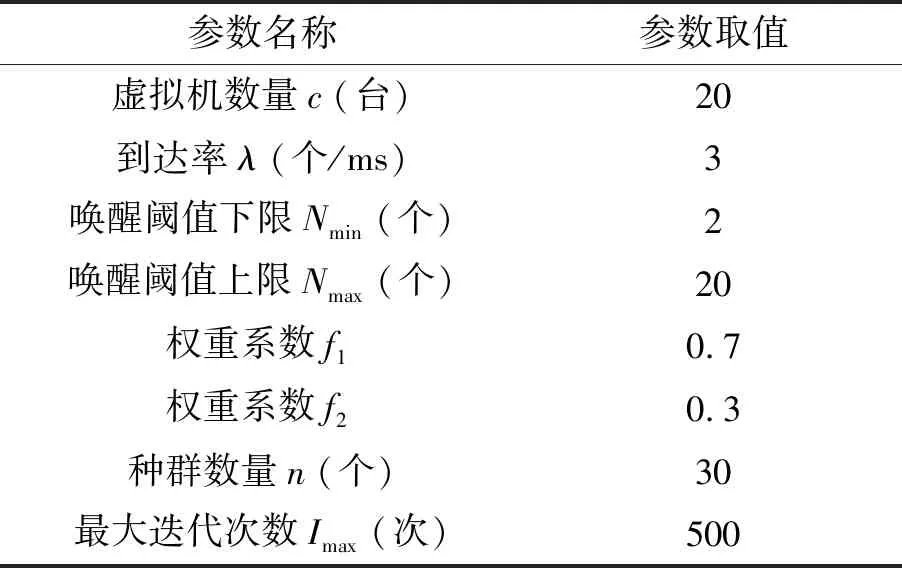
5 结 论

