适用于VSC-HVDC系统的静态电压稳定分析改进方法

吴成业，李 飞，刘光晔

(1.安徽工业大学 电气与信息工程学院，安徽 马鞍山 243032；2.湖南大学 电气与信息工程学院，湖南 长沙410082)

随着大规模分布式能源并网、大容量远距离输电的发展，基于电压源换流器的高压直流输电(VSC-HVDC)技术受到了广泛的关注[1-5]。在纯交流系统中，电压稳定问题一直是电力系统研究普遍关注的重要课题之一[6]。对于VSC-HVDC系统，目前其研究大多集中在系统的潮流计算[7-8]、可用输电能力计算[9-10]以及VSC控制器设计[11-12]等方面，而关于系统静态电压稳定的研究方法还很少。

静态电压稳定问题的关键是求取PV曲线中的鞍结分岔点，而连续潮流法[13]一直是求取PV曲线的重要工具。对于含VSC-HVDC的交直流混合系统，文献[14]和文献[15]均通过连续潮流法求得了初始点到电压稳定鞍结分岔点间的PV曲线。由于潮流计算均采用交替求解法，因此其与交流系统中连续潮流法的区别主要是校正环节需要计算交直流网络间的传输功率。

而在纯交流系统中，文献[16]提出了一种基于泰勒级数思想的PV曲线快速求取方法。该方法通过将系统功率展开为关于节点电压幅值的泰勒级数，根据电压稳定鞍结分岔点处功率参数关于节点电压的导数为零的特性，可快速求取电压稳定临界点，同时选择电压幅值为自变量，解决了泰勒级数法在极限点处截断误差大的问题。然而该方法会产生计算误差的两个缺陷。一是泰勒级数展开点的选择存在问题。理论上展开点离极限点越近，曲线拟合得到的鞍结分岔点计算结果越精确，而该方法是直接在距离极限点较远的基态潮流处进行泰勒级数展开的。仿真得到了较精确的结果，是因为计及无功约束时将PV曲线进行了分段处理，客观上将最后一段包含鞍结分岔点曲线的初始点往极限点处拉近了。二是在绘制非光滑PV曲线时，由于每段曲线(第一段除外)的初始点都是上一次泰勒级数的拟合结果，其误差虽然很小，但是会产生误差的传播，不利于最后电压稳定鞍结分岔点的精确计算。

对于VSC-HVDC系统，虽然其系统结构和参数都与纯交流系统不同，但其PV曲线本质上还是描述负荷节点电压幅值关于系统功率的函数关系，因此文献[16]中的泰勒级数法同样可以应用到混合系统求取电压稳定鞍结分岔点。为了消除文献[16]中的两个缺陷，本文在建立泰勒级数法求解VSC-HVDC系统静态电压稳定问题模型的基础上，通过泰勒级数展开点的选择，减小电压稳定鞍结分岔点的截断误差。同时用连续潮流法求取初始潮流点与泰勒展开点之间的计算量较小的PV曲线，然后用泰勒级数法快速求取后半段计算量大的PV曲线，消除传播误差。对修改后的IEEE14节点VSC-HVDC系统进行仿真，验证本文方法在VSC-HVDC系统中的适用性。

1 稳态特性与潮流计算模型

1.1 VSC-HVDC系统稳态模型

VSC-HVDC系统结构如图1所示。它主要由交流系统、直流网络以及电压源换流器组成。

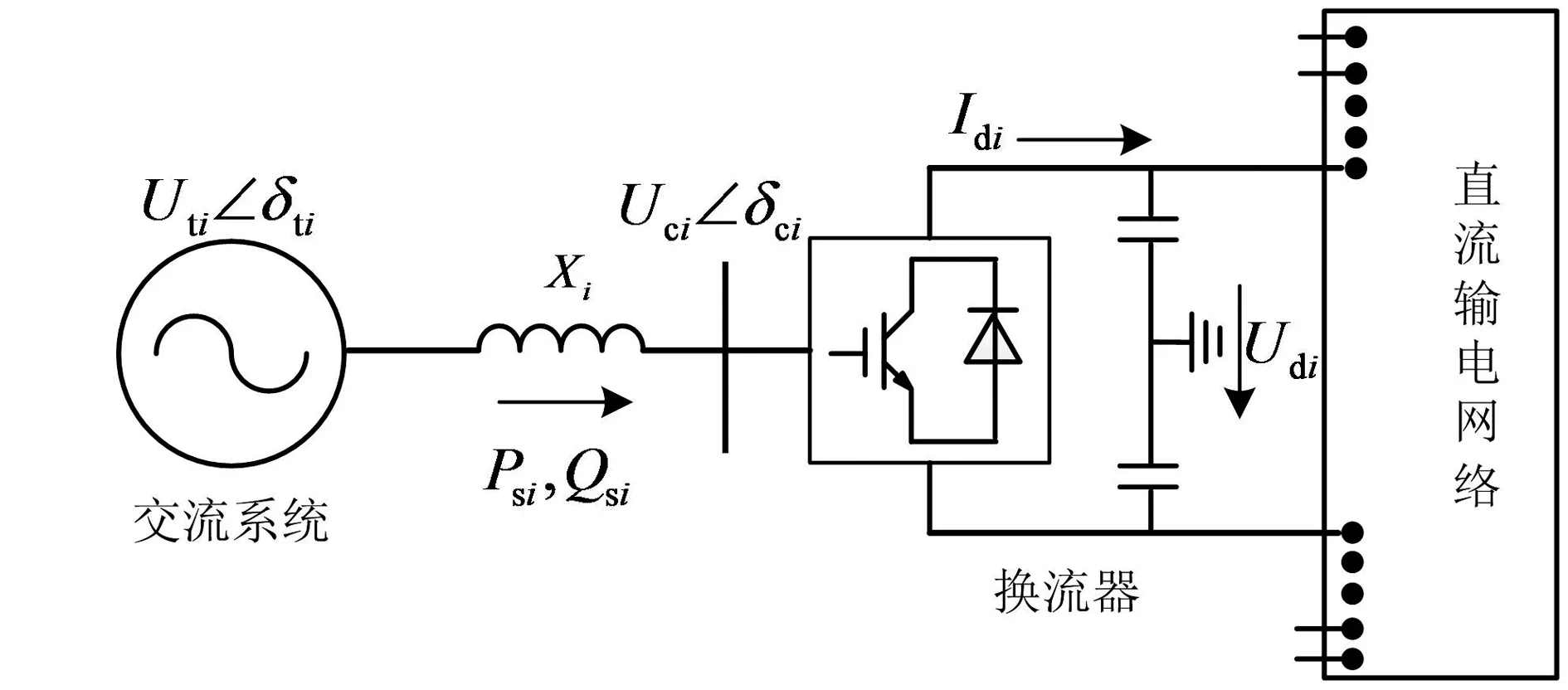
图1 VSC-HVDC 系统模型

其中Xi为忽略换流器电阻的等效电抗，令换流器与交流侧的相角差为δi=δti-δci，可得到交流系统与换流器之间的传输功率为

(1)

(2)

由于换流器采用PWM整流技术，其交流电压幅值与直流电压利用率μ和调制度M有关，即

(3)

由式(1)—式(2)可以看出有功功率传输主要取决于δ，无功功率的传输主要取决于Uc，即由调制度M决定。因此，通过对δ、M的控制便可实现系统对有功功率和无功功率大小和方向的同时控制。

1.2 VSC-HVDC系统潮流计算模型

潮流计算本质上是一个在已知方程条件下求解未知变量的问题。对于VSC-HVDC系统，其潮流方程包括三个部分：

1)在交流系统中，对于与换流器相连的节点有功率方程

(4)

(5)

对于纯交流节点(用下标a表示)，有功率方程

(6)

(7)

2)在直流系统中，有网络方程

0=Idi-∑gdijUdj

(8)

式中gdij为直流网络的导纳矩阵元素。

3)对于电压源换流器，由式(1)—式(3)可得

0=Psi-βiMiUtiUdisinδi

(9)

(10)

0=UdiIdi-βiMiUtiUdisinδi

(11)

式(4)—式(11)为VSC-HVDC系统潮流计算所需的全部方程。需说明的是，方程中共包含10个所需求解的变量，而VSC-HVDC系统潮流计算根据换流器的控制方式[7-10]消去其中两个变量。

本文采用统一迭代法，将式(4)—式(11)线性化得到基于牛顿法的潮流计算修正式为

(12)

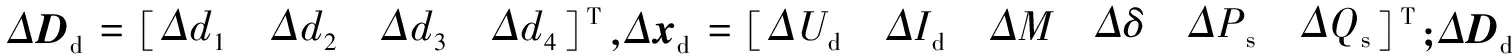
2 连续潮流法与泰勒级数法

2.1 连续潮流法求泰勒展开点前的PV曲线

设VSC-HVDC系统中，节点功率都是功率参数λ的函数，由式(4)—式(11)得到VSC-HVDC系统电压静态稳定分析的数学模型为

W=F(X)

(13)

式中：

X=[θa,θt,Ua,Ut,Ud,Id,M,δ,Ps,Qs]T;X同样根据换流器控制方式需消去两个变量。

假设图2是该系统中某负荷点的PV曲线，其中λ1为本文所定义的泰勒展开点。

图2 负荷节点的PV曲线图

利用文献[15]中的连续潮流法求λ0与λ1之间的PV曲线。由于本文采用统一迭代法进行潮流计算，交直流网络间的传输功率当做系统变量处理，因此校正环节无需再进行传输功率的计算。同时该段曲线离极限运行点较远，因此连续潮流法中可以选取较大步长，且整个过程无需进行参数化处理。可见该段PV曲线的计算量很少。

当负荷接近临界值λmax时，由于雅克比矩阵奇异，为了得到λ1与λmax之间PV曲线，连续潮流法需做参数化处理，且步长控制得很小，该段曲线的计算量是很大的。因此本文采用文献[16]中的方法求取该段曲线。

2.2 泰勒级数法求泰勒展开点后的PV曲线

文献[16]中已经说明用泰勒级数拟合某一函数时，为了拟合结果精确，要求函数为单值函数。因此本文以节点电压幅值为自变量，而系统功率参数为因变量，则可得到如图3所示的PV曲线。

图3 电压为自变量的PV曲线图

分析图3中的曲线,每一个负荷节点的电压幅值U都对应一个系统功率参数λ，即功率参数是负荷节点电压幅值的函数，

λ=G(U)

(14)

泰勒级数是可以将任意形式的可导函数表示成简单且易于分析的幂级数。将曲线所蕴含的函数关系在U1处展开成泰勒解析多项式，即

(15)

在电压稳定临界点处，系统功率参数λ关于节点电压幅值U的导数为零，可由式(15)快速求出电压稳定临界点(Ucr,λmax)。

需说明的是，本文中泰勒展开点λ=λ1是距离极限点较近的点，系统中无功支持较弱的PV节点已全部转换为PQ节点，且VSC-HVDC系统中其他不等式约束量对于系统功率从λ1增长到λmax的这一较短过程不起约束作用。即λ1到λmax之间的PV曲线是连续可导的。

3 电压稳定临界点的求取

3.1 功率参数关于节点电压幅值的泰勒级数

对式(13)两边同时关于λ求1—3阶导数可得

(16)

式中：定义d0Jvsc/dλ0=E为单位矩阵；而Jvsc=∂F/∂X，正好是初始潮流计算的雅可比矩阵。再由式(16)可得系统中各个变量关于λ的1—3阶导数为

(17)

至此本文得到了VSC-HVDC系统中各个变量关于功率参数λ在泰勒展开点λ=λ1处的1—3阶导数，而其中包含各负荷节点电压幅值U关于功率参数λ的导数。为了得到式(15)形式的泰勒解析式，可利用反函数的求导法则，求出系统功率参数λ(Ui)关于各个负荷节点电压幅值Ui的泰勒级数幂次项系数为

(18)

由此得出功率参数λ关于各个节点电压幅值Ui在泰勒展开点λ=λ1处的3阶泰勒展开式为

(19)

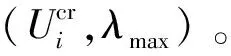
3.2 泰勒级数展开点的选择

设任意一个在定义域内可导的单值函数为

y=f(x)

(20)

令其在x=x1处的泰勒展开式为

y=f(x1)+α1(x-x1)+α2(x-x1)2+

α(x-x1)3+…

(21)

当用式(21)计算y在x=x2处的值时，为了使泰勒级数计算的结果尽可能精确，有两种途径。一是增加泰勒级数的幂次项系数；二是缩小x1与x2之间的距离，即减小Δx=|x1-x2|。

由于VSC-HVDC系统潮流计算的雅克比矩阵中各个变量之间不是简单的线性关系，其关于功率参数的3阶以上导数的计算已十分繁琐，因此泰勒展开点λ=λ1的选择比较关键。要求λ1尽可能接近其极限功率λmax，而潮流方程不奇异。

连续潮流计算过程中，在接近电压稳定临界点时，步长会显著变小，且之后每次步长值之间的数值差也很小。本文采用自适应步长控制，令第n次的步长计算值为σn，若有

(22)

则表明已接近电压稳定临界点，式中ε为判别精度，根据步长控制方法一般有ε=0.1～0.5。而此时功率参数所对应的值λn便是本文方法中的泰勒级数展开点λ1。

4 仿真算例

4.1 修改后的IEEE14 节点系统算例分析

以修改后的IEEE14节点VSC-HVDC系统进行仿真，其系统结构示意如图4所示。

图4 修改后的 14 节点系统

在该系统中2号节点与4号节点之间用VSC-HVDC系统相连，其直流电导gd24=33.33。2号节点为PV节点，令与其相连的电压源换流器VSC1控制方式为定直流电压Ud2=2.000 0、定交流母线电压Ut2=1.045 0，4号节点为负荷节点，令与其相连的电压源换流器VSC2控制方式为定交流有功功率Ps4=-0.360 0、定交流无功功率Qs4=-0.018 0。

假令两个换流器的结构参数相等，其等效电抗X=0.15，直流电压利用率μ=1。VSC-HVDC系统的功率增长方式为全部发电机和负荷功率等比例增长，即对于式(13)，有W=λW0。

本文先用连续潮流法求PV曲线，发现当功率参数值为1.75时，步长明显变小，且满足不等式(22)，因此令λ1=1.75为泰勒展开点，然后用泰勒级数法进行后续计算，得到功率参数的泰勒级数式(19)中各个系数的结果见表1。

观察表1中各幂次项系数可以发现，二次项的系数值最大，这与功率是电压的二次函数相符合。由电压稳定临界点处dλ/dUi=0的条件，计算出各个负荷点的电压稳定临界点，与连续潮流法计算所得结果λmax=1.862 5进行比较，见表2。

表1 电压幅值与幂次项系数

表2 IEEE14系统临界电压点计算结果及其误差

观察表2中的数据可以发现，对于电压稳定临界点的计算，两种方法计算结果基本相同，极限功率误差百分比均小于0.5%。另外，本文也对IEEE30系统进行了仿真验证，与文献[16]方法的计算结果比较，本文方法计算精度明显较高。

4.2 VSC不同控制方式下的算例分析

在VSC-HVDC系统中，换流器采用不同的控制方式，其电压稳定的情况也会有所不同。为了分析VSC换流器对系统电压稳定性的影响，本文以图4中的IEEE14节点系统为例。令换流器VSC1的控制方式不变，而分别改变与4号节点相连的换流器VSC2的有功功率和无功功率控制参数Ps4和Qs4，见表3。

表3 换流器VSC2功率控制参数

画出各负荷点在不同控制方式下的PV曲线，其中9号节点的PV曲线如图5和图6所示。

图5 IEEE14系统9号节点改变有功功率控制参数下PV曲线

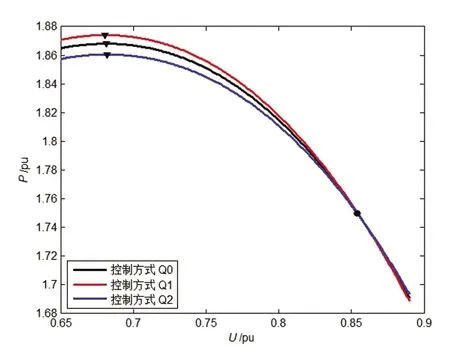
图6 IEEE14系统9号节点改变无功功率控制参数下PV曲线

由图5和图6可以发现，通过控制换流器传输功率的大小可以改变系统的电压稳定性。曲线的顶点越高，说明电压稳定性越高；顶点间距越大，说明影响程度越大。

5 结论

本文将纯交流系统中基于泰勒级数的静态电压稳定分析方法应用到了VSC-HVDC系统并做出了改进。基于泰勒级数法的VSC-HVDC系统的静态电压稳定分析，其难点在于换流器中各直流参数的限制会影响PV曲线的连续性。本文通过将泰勒级数法与连续潮流法相结合，在稳定临界点附近选取泰勒级数展开点，既较大程度地避免了因直流参数限制导致的PV曲线不连续，又改善了泰勒级数法的缺陷，提高了计算精度。