基于扩展卡尔曼滤波算法的二阶电池模型SOC估算
查伟民
(方大新材料(江西)有限公司,江西 南昌 330096)
电池管理系统是电动汽车的关键部件之一,具有电池系统状态监测、故障诊断与保护、均衡管理和绝缘检测等功能。对电池组中单体电池的SOC进行精确地估算,可以为电池管理系统进行能量均衡提供依据与判断,有利于延长电池的使用寿命[1]。
目前常用的SOC 估算方法有开路电压法、安时积分法、神经网络法和卡尔曼滤波算法等[2]。开路电压法需要长时间静止测得电池两端开路电压(OCV),再通过查表形式或者多项式形式确定对应的SOC值。安时积分法可以精确地估算电池的SOC,但是此方法需要精确的初始SOC值,不能避免错误的初始SOC所带来的误差。神经网络算法需要大量的历史试验数据来进行训练与预测,该方法计算量十分庞大,在计算能力差的硬件上很难应用[3-6]。国内外利用卡尔曼滤波算法对电池SOC估算方面进行了大量的研究,主要有扩展卡尔曼滤波算法和无迹卡尔曼滤波算法等。本文主要运用MATLAB/Simulink平台对电池的二阶模型进行了建模,运用MATLAB工具箱中的最小二乘法对电池模型参数进行了辨识,然后再利用扩展法卡尔曼滤波进行SOC估算,并对结果进行了分析与讨论。
1 电池等效电路模型
电池等效电路模型主要有PNGV模型、Thevenin 模型、二阶RC 等效电路模型以及N阶RC等效电路模型等。一般情况下随着RC个数增加,模型就越精确;但是随着RC个数增加,所需要辨识的模型参数也就越多,相应的计算量也会增大[7-10]。为平衡模型精度和计算量,本文选取二阶RC模型作为电池模型来进行仿真与估算,如图1所示。

图1 二阶等效电池模型
电池的剩余电量估计是电池管理系统的关键技术之一,其能够直观的反映电池的荷电状态。美国先进联合会(USABC)从电量角度将电池荷电状态SOC定义为:在一定放电条件(恒流、恒温)下,电池剩余容量与相同条件下额定容量的比值。
(1)
式中:SOC(t)表示t时刻的SOC值,SOC(t0)表示t0时刻的SOC值,η表示库伦效率,这里η=1,I表示输入的电流,Qn表示电池额定容量。根据电路的基尔霍夫定律可知,二阶模型可以由式(2)来表示:
(2)
式中:R0为电池模型欧姆内阻,R1和R2为电池模型极化内阻,C1和C2为电池模型极化电容,U1和U2分别为R1和R2两边的电压,Ut为电池的端电压,Uoc为电池的开路电压,It为流过电池的电流。
2 电池模型的参数辨识
在进行仿真与估算之前,需要对二阶RC等效电路模型进行参数辨识,本文主要运用离线辨识的方法对二阶模型进行参数辨识。首先对电池进行混合脉冲功率特性工况(HPPC)放电实验,实验电池为NCR18650电池,脉冲电压曲线如图2(a)所示。现选取单个脉冲对电池模型进行参数辨识,如图(b)所示。电压从A点到B点的突然下降主要是由电池欧姆内阻所引起的,电压从B点到C点主要是由极化电容的迟滞效应所引起的,当电流突然卸载之后,由于欧姆内阻的作用,由C点瞬间上升到D,然后再由D点缓慢上升,直至平稳。
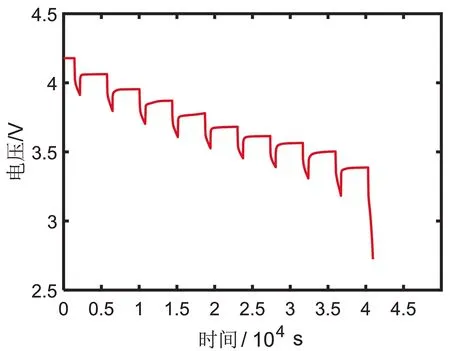
(a)采集的电压曲线
这一过程中欧姆内阻R0可由式(3)表示:
(3)
式中:R0为电池欧姆内阻,I为输入电流。
从C点到D点直至平稳过程中,电池端电压可以表示为:
V=VOC-V1(0)e-t/R1C1-V2(0)e-t/R2C2
(4)
式中:V1为电路模型中R1C1端的电压,V2为电路模型中R2C2端的电压。
由A点到C点过程中,电池端电压可以表示为:
V=VOC-IR0-IR1(0)e-t/R1C1-IR2(0)e-t/R2C2
(5)
在C点处,RC并联网络的电压等于式(4)中的初始电压,即
(6)
根据式(4)、(5)和(6),利用MATLAB的cftool工具箱[11],辨识出二阶模型的各个参数,见表1。

表1 放电过程中模型离线参数辨识结果
在单个HPPC脉冲放电工况中,放电完成后经过长时间静止,可以将此时的电压作为电池OCV,因此记录每次脉冲放电后的SOC值与其对应的OCV值,两者的关系可以由六次多项式来表示,拟合曲线如图3所示。
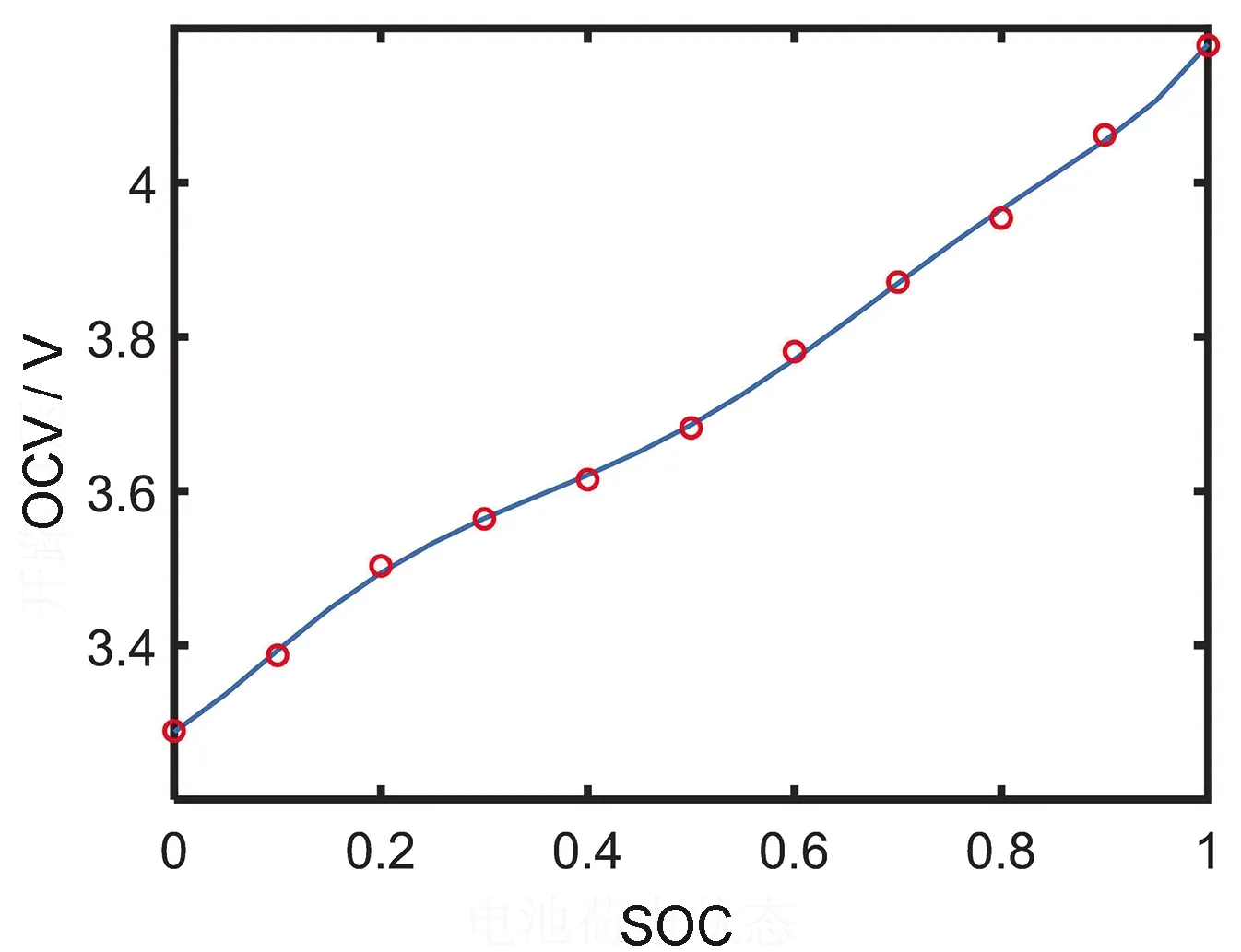
图3 OCV-SOC拟合曲线图
电池的SOC-OCV关系可以由式(7)来表示:
Uoc=19.068SOC6-56.276SOC5+
60.844SOC4-28.32SOC3+4.766SOC2+
0.809SOC+3.288
(7)
3 扩展卡尔曼滤波算法的SOC估算
扩展卡尔曼滤波算法和无迹卡尔曼滤波算法都能对非线性系统进行最优状态估计,本文只利用扩展卡尔曼滤波算法进行电池的SOC估算。扩展卡尔曼滤波的基本思想是利用泰勒公式在状态估计值处对非线性系统进行一阶泰勒展开,将系统线性化,然后运用卡尔曼滤波算法对系统状态进行估算。
根据式(2)可以将电池模型状态方程和观测方程转化为:
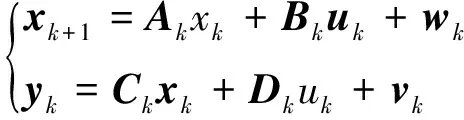
(8)
式中:wk为过程噪声,其均值为零,方差为Q的高斯白噪声,vk为观测噪声,也是均值为零,方差为R的高斯白噪声,ΔT为采样时间,这里为1 s。
Ck=[-1-1dUoc(SOC)/d(SOC)]Dk=-R0
xk=[U1(k)U2(k)SOC(k)]
uk=I(k)
卡尔曼滤波算法的步骤如下:
(9)
(2)状态预测
(10)
(3)协方差预测
(11)
(4)计算卡尔曼增益
(12)
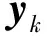
(13)
(6)更新状态
(14)
(7)协方差矩阵
(15)
4 仿真结果与分析
通过MATLAB/Simulink平台建立电池二阶等效模型,并利用扩展卡尔曼滤波算法对电池SOC进行估算。实际电池测试中,先将电池充满电,因此实际中的SOC为1,参考SOC值可以用安时积分法在无噪声的情况下来计算,可视为理想SOC值。图4为EKF算法流程图。在HPPC工况下,实际的SOC值与EKF估算SOC值及误差值如图5(a)和(b)所示,从图上可以看出,EKF算法估算的SOC与实际值误差不大,很好的追踪了实际的SOC值,通过计算可得,最大绝对误差值为0.019 8,平均绝对误差值为0.006 4,平方根绝对误差值为0.08。实际测量的电压值与EKF估算的电压值及误差值如图6(a)和(b)所示,从图中可以看出实际测量的电压值与EKF估算的电压值相吻合,其最大绝对误差值为0.059 8 V,平均绝对误差值为0.002 V,平方根绝对误差值为0.045 V。
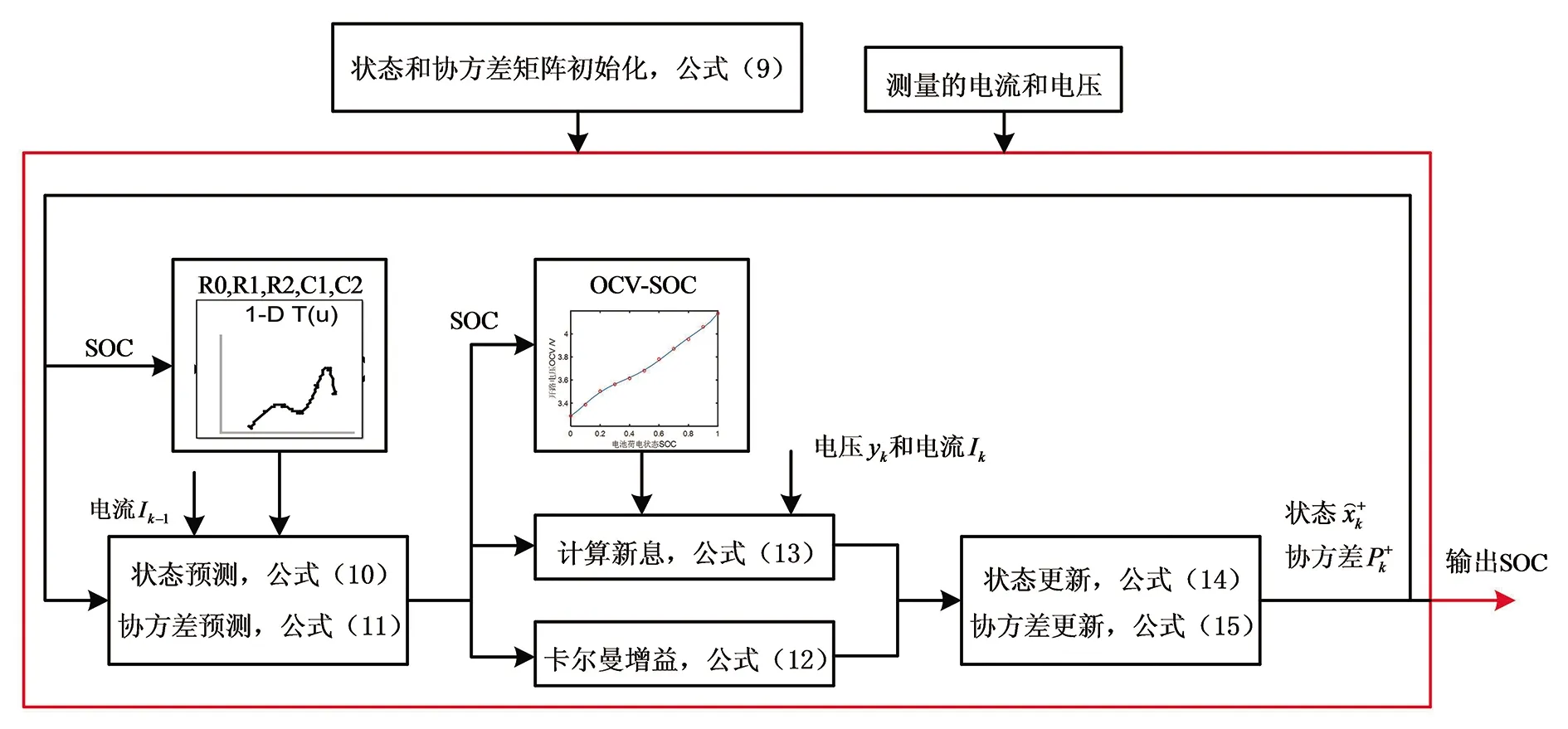
图4 EKF算法流程图
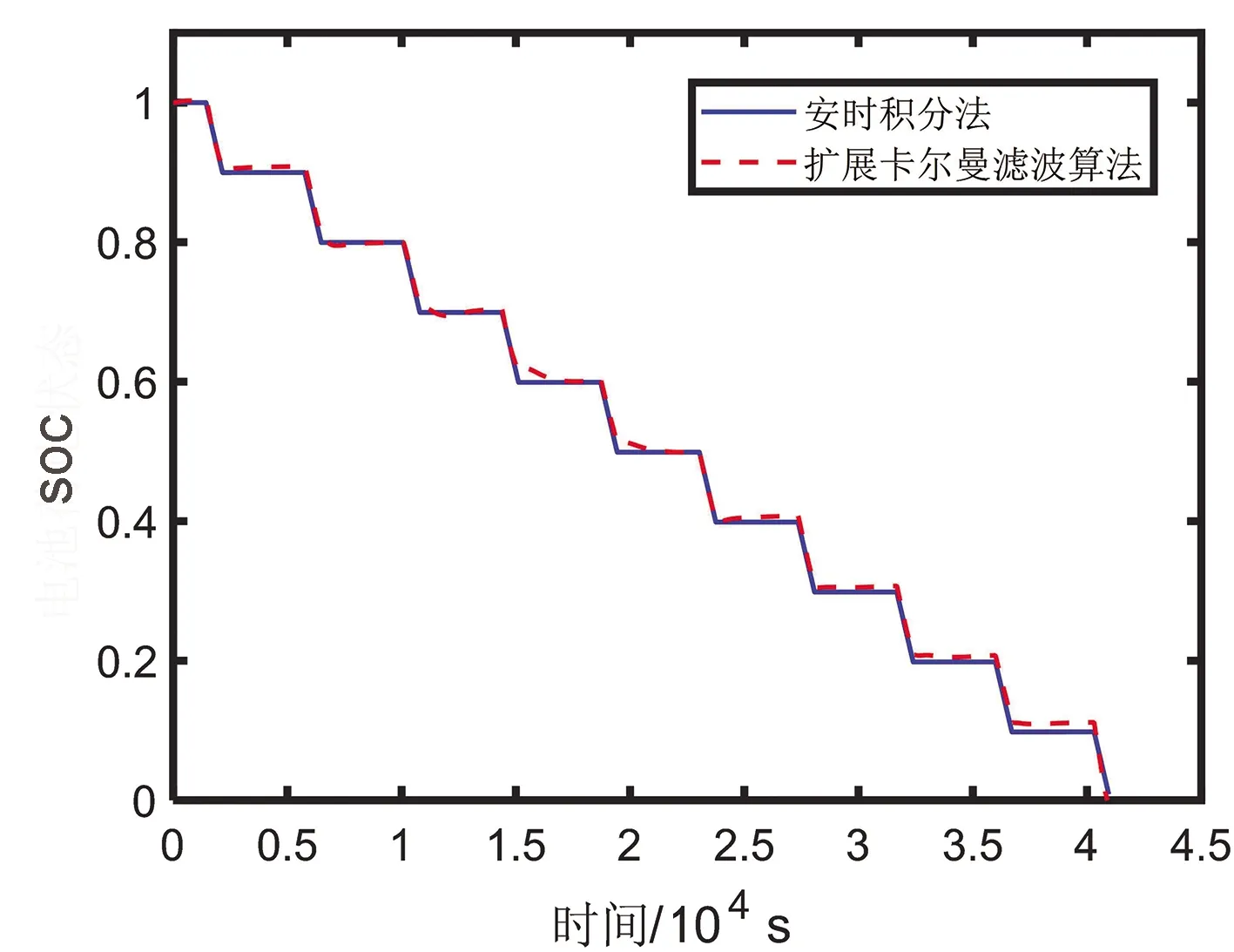
(a)EKF算法估算SOC曲线
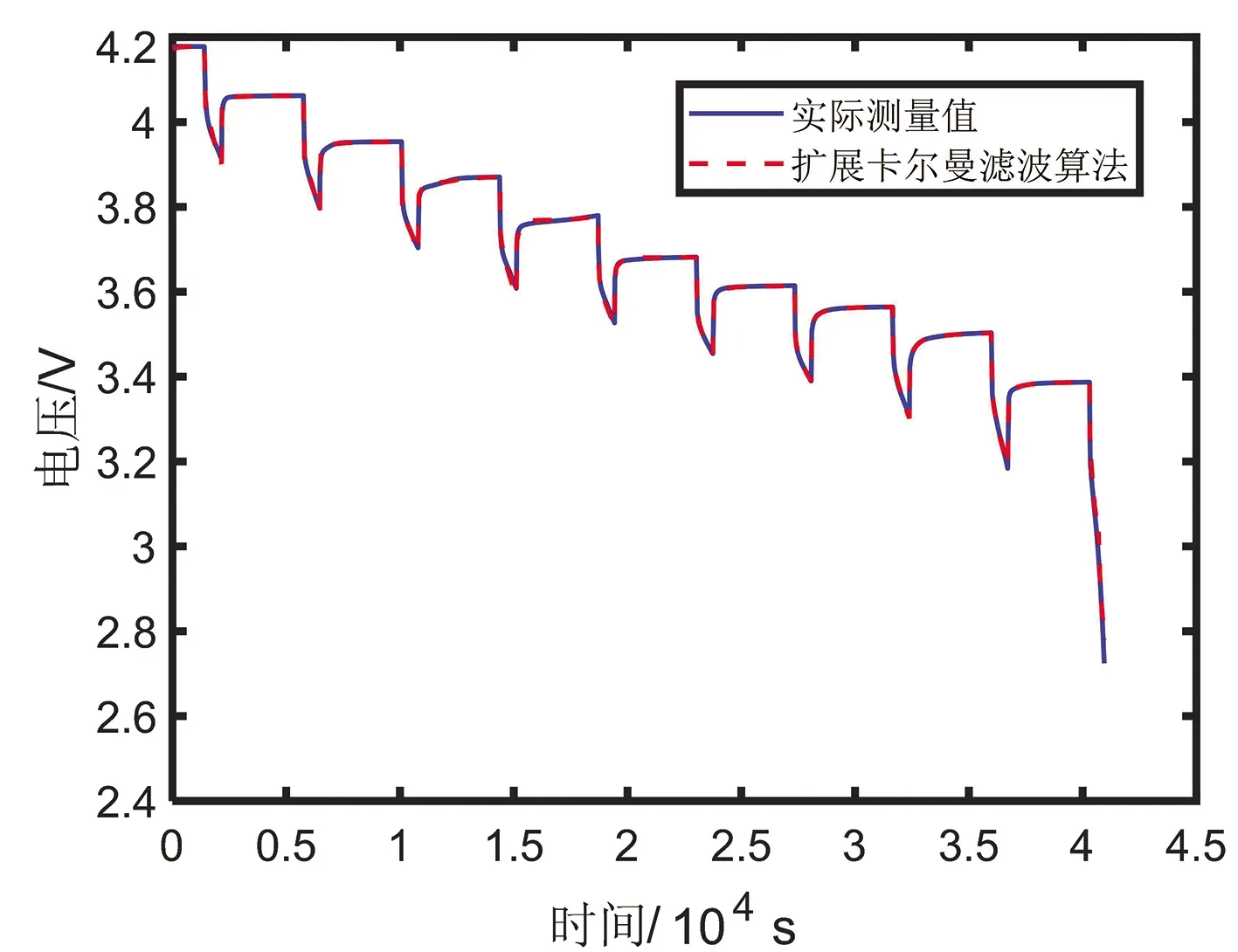
(a)EKF算法电压预测曲线
为检验EKF算法在电池SOC估算方面是否具有鲁棒性,现将初始的SOC值假设为0.9,然后再利用EKF算法对HPPC工况进行仿真与分析。SOC估算结果如图7(a)和(b)所示,从图中可以看出,即使初始SOC值不确定的情况下,EKF算法也能够很好的追踪实际的SOC值,以误差为0.05为基准点,EKF算法将在351 s时得到收敛,通过计算得知平均绝对值误差为0.007 3,均方根绝对误差为0.085 3。电压估算曲线如图8(a)和(b)所示,从图中可以看出,电压估算曲线在SOC初始值不确定的情况下也能很好的追踪实际的电压曲线,其平均绝对误差值为0.003 2 V,平方根绝对误差值为0.057 V。
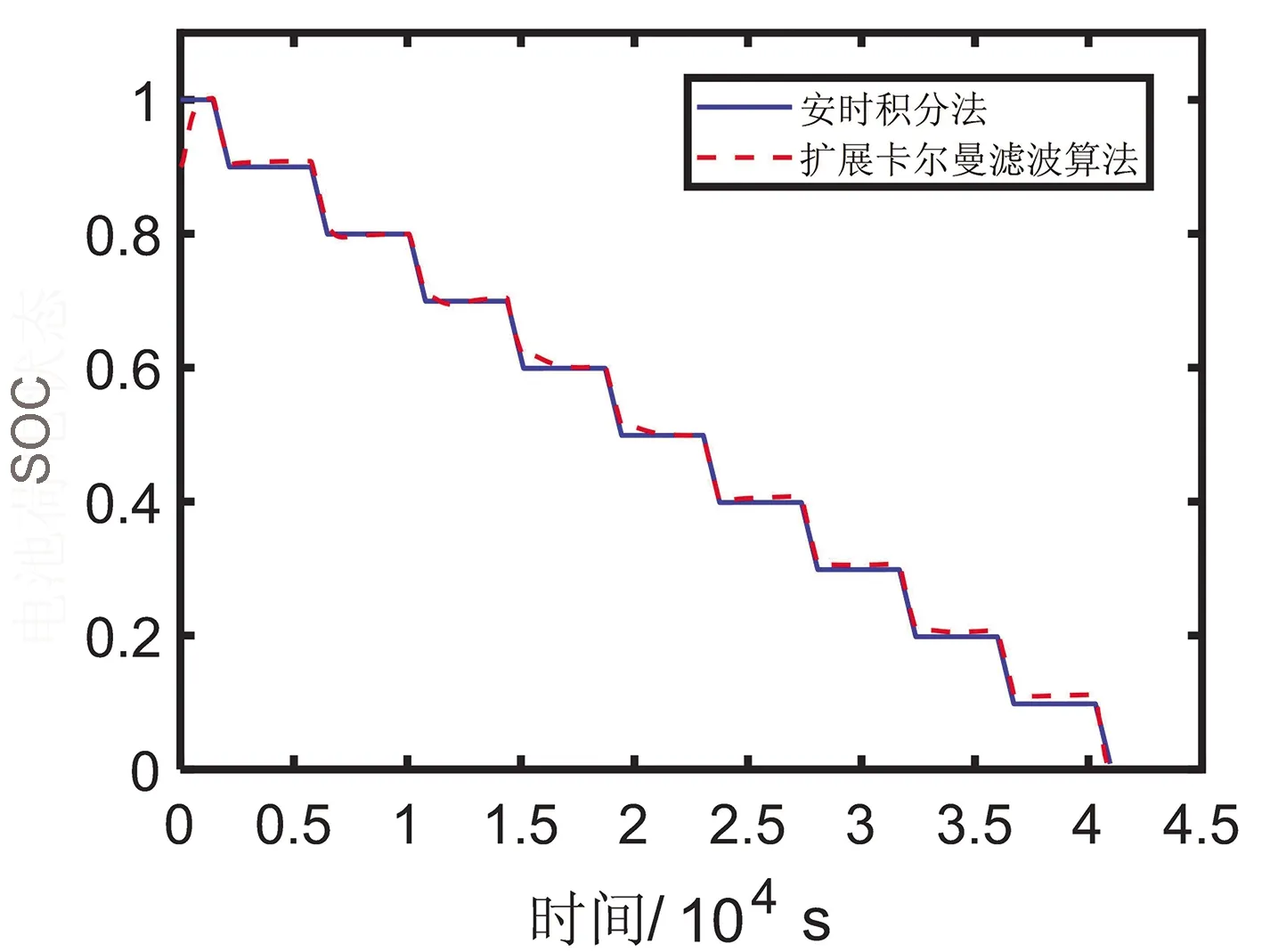
(a)EKF算法估算SOC曲线

(a)EKF算法电压预测曲线
5 结束语
本文以锂离子单体电池为实验对象,进行了HPPC工况脉冲放电实验,再通过MATLAB/Simulink仿真平台对其进行了等效电路模型的建模,并通过最小二乘法参数辨识原理对二阶模型的各个参数进行了离线参数辨识,最后利用扩展卡尔曼滤波算法对电池等效电路模型进行了SOC与电压估算。在准确初始值和假设初始值两种情况下进行仿真验证,单体电池的SOC误差在0.01以内,电压估算误差在0.005 V以内。在初始值不确定的情况下,电池SOC曲线与估算电压曲线也能够快速收敛于真实值,这表明EKF算法在电池SOC估算方面具有精度高、收敛快和实用性较强的优点。未来的工作中,电池健康状况将成为主要研究方向。该算法还需进行硬件在环测试,以验证其在实际工作中的效果。

