赛车车架动态特性仿真、测试与评价

王 丽， 李长玉， 戴海燕， 李淼林

（华南理工大学广州学院汽车与交通工程学院，广州510800）

0 引 言

振动现象是工程结构系统经常遇到的问题之一，在外界激励（动态载荷）的作用下，机械结构会发生振动，研究机械结构在动态载荷作用下的振动特性，即动态特性。国内外学者对于机械结构的动态特性研究较多。国外学者Harak等［1］以缓冲器和缓冲垫片为研究对象，采用自由模态分析和约束模态分析的方法，改进了缓冲器的结构。SUN等［2］以工业生产中应用广泛的薄壁件为研究对象，进行振动模态测试，以提高其模态特性。廖宁波等［3］以卫星扬声器振膜作为研究对象，采用ANSYS Workbench仿真软件对微型扬声器振膜进行了有限元分析，并利用模态分析得出振膜的各阶固有频率和振动形态，提升了振膜性能。朱梦等［4］对工业机器人的核心零件RV减速器进行了有限元仿真和模态分析，并通过实验验证了仿真结果的可靠性，为后续研究结构的动态特性提供了参考。伍济钢等［5］对光流点匹配跟踪的薄壁件进行了有限元仿真和振动模态测试，获得了薄壁梁的固有频率和模态振型。朱茂桃等［6］利用动态性建模与仿真分析方法，开发了一种具有阻尼切换功能的两级阻尼半主动液压减震器。仇高贺等［7］对全地形车架建立有限元模型并获得固有模态参数，分析了满载工况时车架频率响应特性和怠速工况时发动机振动对车架动态性能的影响。李长玉等［8］对车辆排气系统进行了有限元仿真和模态分析，分析了该排气系统动态特性。

有限元法和模态分析作为动态特性分析方法，能较好地解决行业中的可靠性、耐久性等问题，模态分析在赛车车架的设计中也逐步开始运用［9-12］。机械结构的模态分析有仿真模态分析和实验模态分析两种。赛车车架设计一般采用软件仿真模态分析。本文以中国大学生方程式汽车大赛赛车车架为研究对象，探讨赛车在行驶过程中来自路面和发动机常用工况的激励频率对整个车架产生的振动，采用仿真模态分析和实验模态分析相结合的方法，研究其动态特性，获得了其前6阶模态参数。对实验模态分析结果和仿真模态结果进行了对比分析，模态振型和固有频率是一致的，具有较好的动态特性。

1 赛车车架结构

1.1 赛车车架有限元建模

某赛车车架属于非承载式车身，其结构分前舱、驾驶舱和发动机舱3部分，结构示意图如图1所示。前隔板与前环之间为前舱、前环和主环之间为驾驶舱，主环之后为发动机舱。

利用CATIA软件建立车架初始模型。车架钢管的建模采用CATIA扫略命令，直接将线框扫出圆柱面，在零部件设计中，将圆柱面增厚成管状即可。对于前舱和驾驶舱，先建模出主环和前环，导入95%的人体模型调节前舱和驾驶舱的尺寸，可建模出前舱和驾驶舱的框架。对于发动机舱，将发动机模型导入CATIA以此确定发动机舱的轮廓。

图1 某赛车车架结构示意图

CATIA人体模型的依据是人机工程学。实际操作时，将CATIA人体模型置于1∶1空间模型，如图2所示，进行校核，验证其合理性和可行性。根据实际赛车手驾驶姿势的人体生理角度，包括人体尺寸、作业尺寸（手腿操控范围）等，确定相应的驾驶舱和前舱的尺寸、座椅位置、方向盘等参数（见表1）。7．83 g／cm3，屈服强度高，可达到680 ～695 MPa，力学性能好；且4130的Cr铬和Mo钼的含量比较高，材料比较坚硬，碳的含量比例适中，特别适合焊接。因此该赛车车架材料选用4130钢管。

图2 加载人体模型后的1∶1车架空间模型

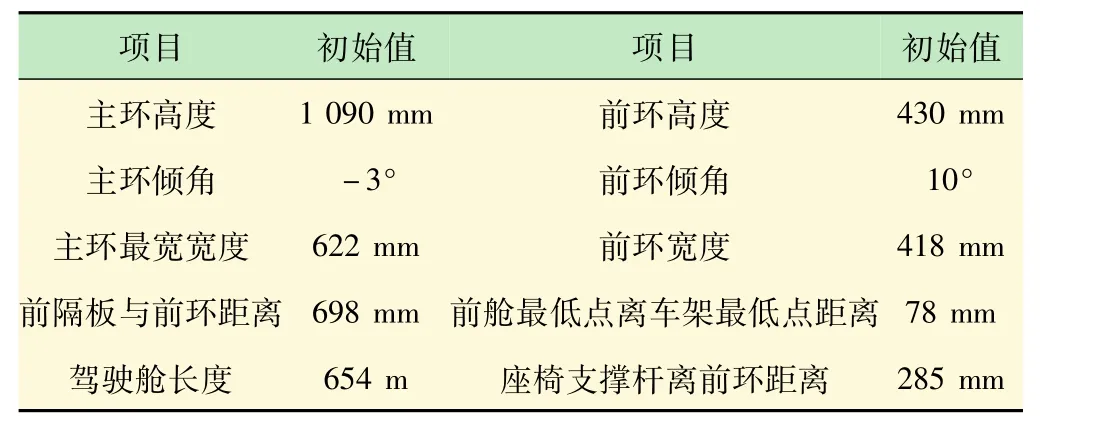
表1 人机车架尺寸

建立高质量的有限元模型是ANSYS前处理非常重要的一步，构建的模型越真实，分析误差就越小，网格的划分非常关键。赛车车架选用4130圆钢管，用梁单元划分网格。设置单元格大小为1 mm，自动生成网格。在不影响结果精度的前提下对模型进行简化，为最大限度地减少误差，依据小特征网格细化原则，用直线代替车架中钢管弯曲的几何结构增加网格密度，力求结果精确并提高求解效率。在CATIA做好车架的线体后，导入ANSYS。

1.2 车架仿真模态分析

利用已建立的有限元模型，加载约束为固定悬架所有硬点。采用ANSYS软件进行仿真模态分析。为了能准确地描述系统的动态特性，设置求解系统的模态振型。低阶模态振型相对高阶振型对机械结构的影响较大，因此本研究中计算前6阶模态振型。

2 车架振动模态实验

2.1 试验设计

为验证赛车车架结构的动态特性，采LMS-test lab系统（LMS振动试验系统），进行了Test．Lab的Impact锤击法模态测试试验。对于实验采集到的数据，要进行加速度和力时域信号的减噪、时频变换、功率谱计算和模态参数识别等工作，才能得出模态振型。实验中信号的处理和分析利用一般复杂模型的最小二乘复频域模态识别方法（Least squares complex frequency domain method，LSCF）［13］。LSCT 1 采用频响函数矩阵作为识别初始数据，采用右矩阵分式模型描述其数学模型［14-15］：

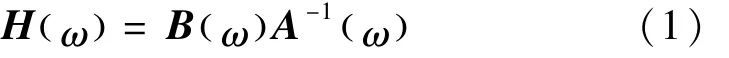
式中：H(ω)为频响函数矩阵，H(ω )∈MNa×Nb。Na为系统输出数，Nb为系统输入数。而A(ω)、B(ω)∈MNa×Nb为矩阵多项式，即

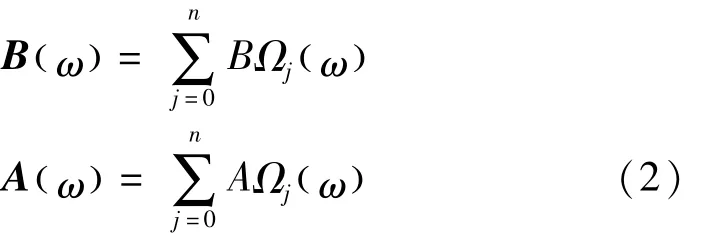
式中：n为模态分析时的模型阶次；Aj、Bj(j ＝0，1，…，n)为矩阵多项式的系数；Ωj(w)为基函数，定义为：

式中，Ts是采样周期。

基于正则方程缩减最小二乘问题，获得压缩正则方程为：

通过求解最小二乘问题得到模态参数。该方法具有较强的抗干扰能力和优秀的识别模态能力，特别是针对复杂机械结构尤为突出，是目前国际上公认的最优秀的实验模态参数识别方法之一。利用LSCT 1［16］分析频率响应函数进行模态识别，即在LMS振动试验系统的Modal Analysis模块对频响函数进行模态参数分析，得到车架前6阶振型和固有频率。

实验模态测试系统如图3所示。

测试采用定点锤击法，即在测试过程中选择某一固定点作为参考点施加锤击，在其他的测试点（又称测点）进行测量并采集数据。赛车车架的振动测试包括发动机舱、驾驶舱和前舱等相关位置，主要测试内容为X（横向）、Y（纵向）、Z（竖直）方向，共实施147 个测点。

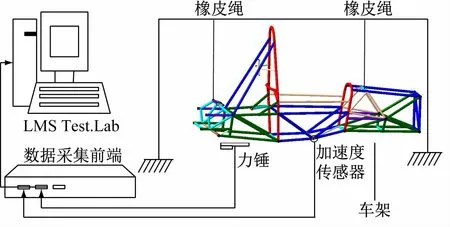
图3 实验模态测试系统示意图

2.2 锤击法模态测试过程

测点工况为了测试整个车架振动的动态特性，选取影响较大的框架布置测点，测点布置情况如图4所示。

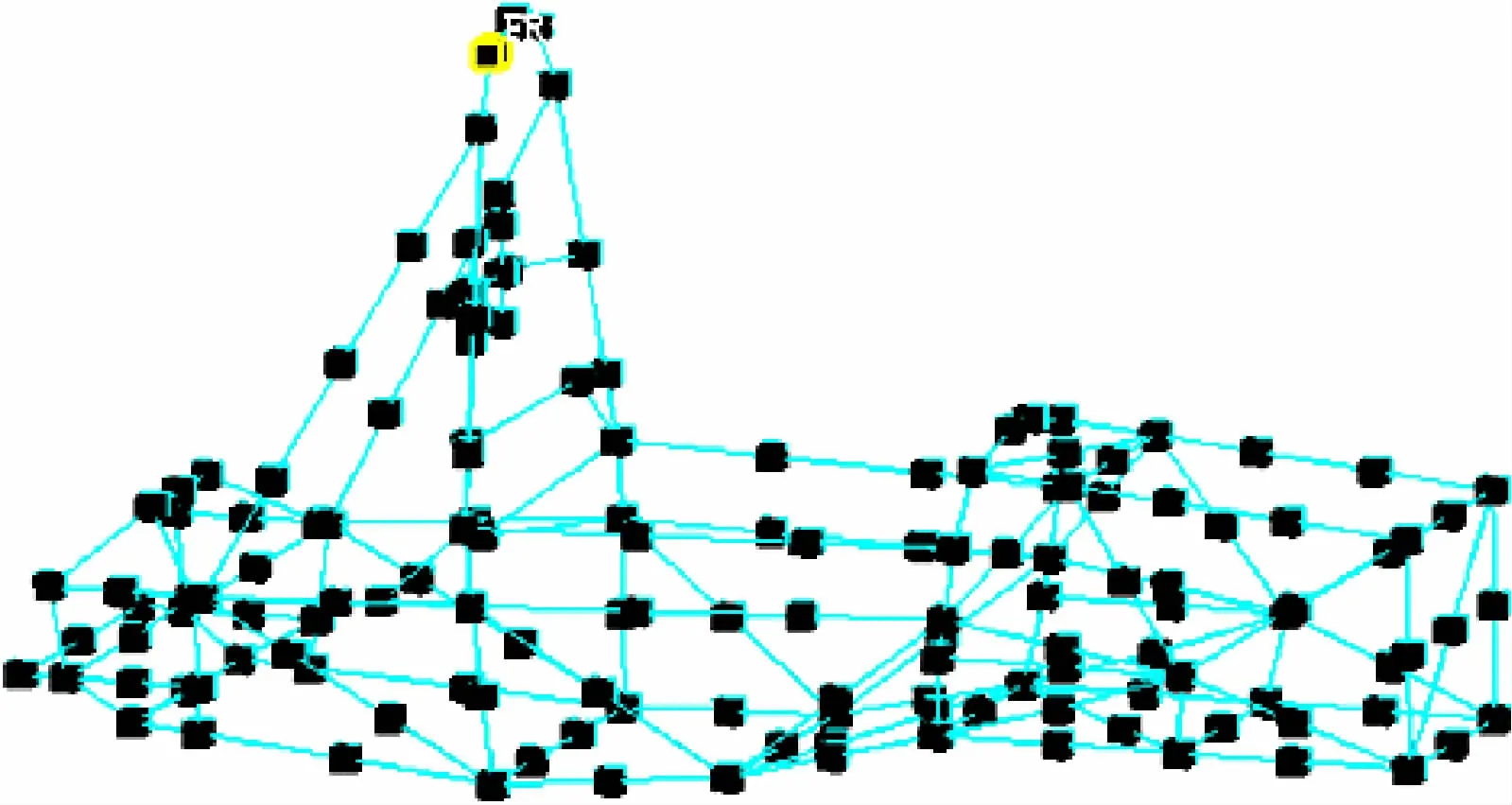
图4 测试系统测点布置图

同时，LMS振动试验系统的Geometry工作表里面车架点线框模型，点的方向要与3向加速度传感器贴的方向一致，且根据车架的实况调节点的欧拉角即方向。

贴好加速度传感器，将车架悬吊并保持水平。连接电脑和LMS振动试验系统的测试设备，并保持各通道畅通，设定初始参数，包括通道设置、锤击示波、锤击设置，开始测量。

在测试时，选取76号测点为参考点，用力锤敲击76号测点。加速度传感器拾取其他测点X、Y、Z 3个方向的加速度信号。根据加速度信号和输入的力信号可计算各点相对于参考点频率响应函数。其中第76号测点3个方向的频率响应如图5所示。

3 对策振型对比分析与评价

3.1 赛车车架固有频率对比

根据仿真模态分析和锤击法模态实验测试得固有频率，分析某赛车车架的动态特性，各阶次的固有频率数据对比见表2。由表2的固有频率对比可见，实验模态分析对比仿真模态分析的固有频率，相对误差最小为4．5%、最大为第5阶的8．55%，前6阶相对误差均在10%以内，两者固有频率吻合度较高。因此，对于该赛车车架在实验模态分析得到的系统固有频率与仿真计算分析得到的固有频率具有较高的一致性。

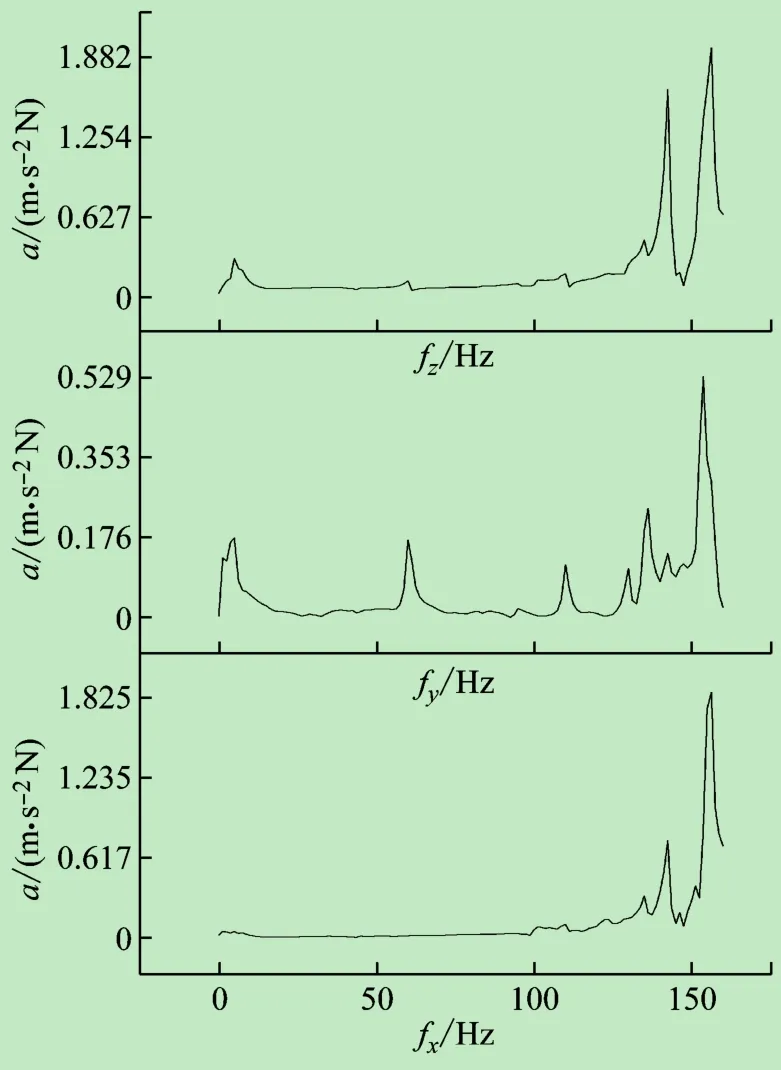
图5 第76号测点频率响应函数图

表2 仿真模态分析与实验模态分析固有频率对比

3.2 赛车车架振型对比

图6～11分别为某赛车车架的仿真模态和实验模态分析的前6阶模态振型图，其中图6～11（a）为各阶的仿真模态振型图，图6～11（b）为各阶的实验模态振型图。

图6为车架的第1阶模态振型，车架整体绕着中后部的Y轴发生垂直弯曲。驾驶舱后部至前环位置上偏移，使得发动机舱、前舱位置有向下偏移趋势，驾驶舱后部的变形较大。通过比较，仿真计算和实验测试的第1阶模态振型重合度较好。

图7为车架的第2阶模态振型，振型绕车架X轴发生弯曲，包含了S形侧向弯曲、轻微的扭转变形，且后端的驾驶舱变形较大。通过比较，仿真计算和实验测试的第2阶模态振型重合度较好。

图8为车架的第3阶模态振型，振型绕车架中部Y轴发生弯曲，即垂直弯曲。前环至前舱发生上偏移，发动机舱下偏移，主环至发动机舱的变形较大。通过比较，仿真计算和实验测试的第3阶模态振型重合度较好。

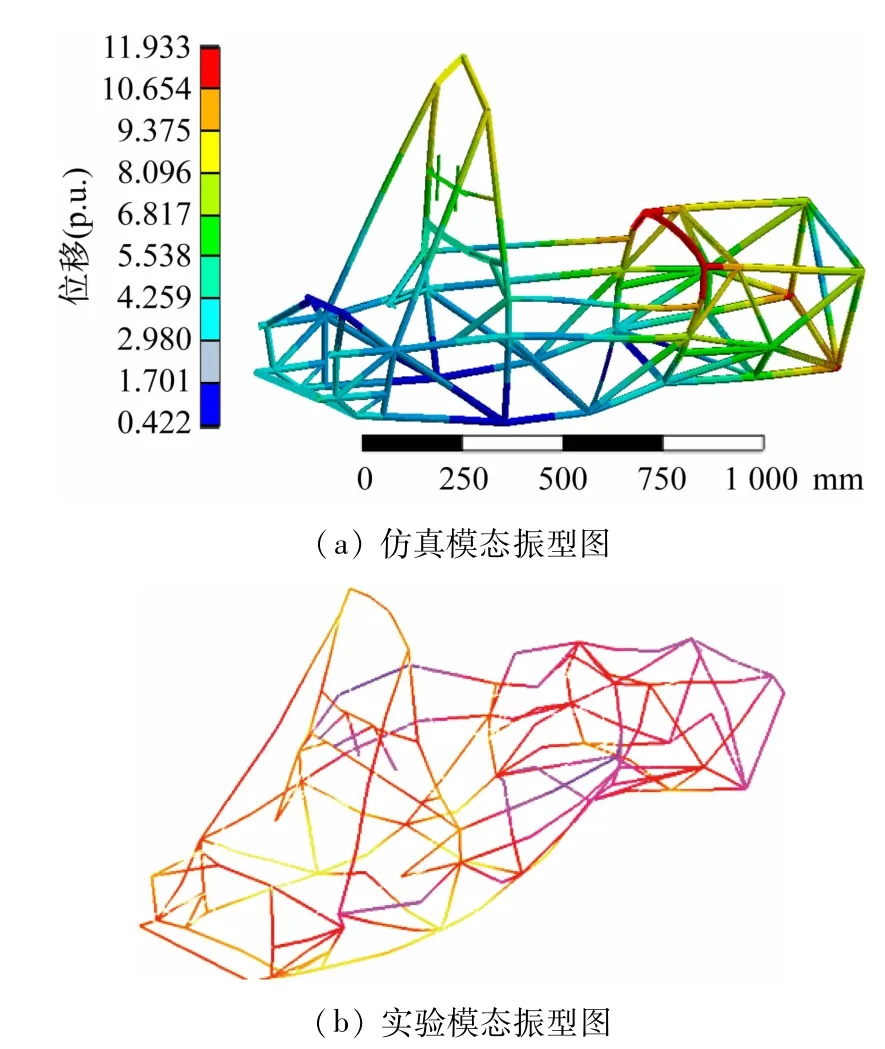
图6 第1阶模态振型对比

图7 第2阶模态振型对比

图9 为车架的第4阶模态振型，振型绕车架中部Y轴垂直弯曲，主环弯曲幅度较大。通过比较，仿真计算和实验测试的第4阶模态振型重合度较好。

图10为车架的第5阶模态振型，振型绕车架X轴和Y轴均有弯曲，既有垂直弯曲，又有侧向弯曲，可以看成是1阶和2阶的综合。通过比较，仿真计算和实验测试的第5阶模态振型重合度较好。

图11为车架的第6阶模态振型，轻微绕车架中部Y轴弯曲，侧边防撞杆以上主环振动较剧烈。通过比较，仿真计算和实验测试的第6阶模态振型重合度较好。

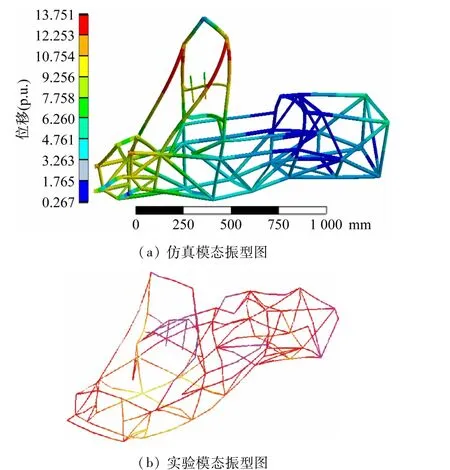
图8 第3阶模态振型对比

图9 第4阶模态振型对比

综上所述，该车架模态振型主要表现为垂直弯曲、侧向弯曲和轻微的扭转。各阶模态振型在固定频率附近实验测试模态和仿真计算模态具有相同的振型，且二者体现的是同1阶模态。

3.3 赛车车架动态特性分析与评价

赛车在实际行驶过程中的激励主要有两种，一是来自路面的激励，二是发动机常用工况对整个车架产生的振动。

由于赛道路面较为平缓，可参考城市交通较好的路面。根据实际，当车速80 km／h左右时，路面激励频率通常为3 Hz以下，车轮不平衡引起的激振频率通常为11 Hz以下。从表3的模态分析结果可知，车架的低阶固有频率高于路面和车辆不平衡引起的激振频率范围。避免了路面激励与赛车车架发生共振。

图10 第5阶模态振型对比

图11 第6阶模态振型对比

发动机激励频率是由发动机转速决定的，发动机激励频率：

式中：n′为发动机转速；i′为发动机缸数；τ为赛车发动机冲程数。赛车发动机型号为4缸4冲程CBR600，根据此发动机相关数据可知，该赛车常用转速为12 000 ～15 000 r／min，由式（5）计算获得对应的振动频率为400～500 Hz；怠速工况下转速为4 000 r／min左右，对应的振动频率为133Hz。对比表2中的固有频率值，这两种工况下前5阶模态固有频率与发动机的激励频率相差较大，第6阶模态的固有频率与发动机怠速工况激励频率相差不大，而怠速时间很短暂，即使发生共振的时间也很短暂，可以忽略。

以实验测试赛车车架的固有频率，根据式（5）计算对应赛车发动机转速，见表3。

表3 某赛车发动机固有频率和转速

由表3可知，该赛车车架前5阶固有频率与外界激励频率相差较远，对应转速小于发动机怠速转速。第6阶模态固有频率对应的赛车发动机转速4 212．48 r／min，相比较该赛车发动机的怠速工况转速4 000 r／min，相差不大，但怠速工况4 000 r／min为不常用转速，且怠速发生时间很短，可以忽略。因此，该赛车车架在前6阶模态很大程度上避免共振现象的发生，该车架具有较好的动态行驶性能。

4 结 语

本文利用仿真计算模态和实验模态对比分析的方法对某赛车车架的动态特性进行了分析和评价。两者误差较小，说明建立的赛车车架有限元模型质量较高，计算结果正确。同时，两者得到的该赛车固有频率与发动机工作激励频率相差较大，可避免工作激励引起赛车车架共振；该赛车车架前5阶固有频率与外界激励频率相差较远，对应转速小于发动机怠速转速，能避开共振，动态特性较好。

本文的方法可应用与赛车车架开发环节，在保证设计赛车车架较好动态性能的同时缩短开发周期，降低开发成本。本文的结论对赛车车架动态特性设计具有一定的指导意义。

·名人名言·

我们应该使每一个学生在毕业时候，带走的不仅仅是一些知识和技能，最重要的是要带走渴求知识的火花，并使它终生不熄地燃烧下去。

——苏霍姆林斯基