基于DBN 算法的热轧高强钢薄板轧机振动预报研究①

董志奎， 梁朋伟， 禚超越， 孙建亮，3， 赵静一， 卢明立

（1.燕山大学 机械工程学院，河北秦皇岛066004；2.江苏天明机械集团有限公司，江苏连云港222002；3.燕山大学国家冷轧板带装备及工艺工程技术研究中心，河北 秦皇岛066004）

钢铁行业是国民经济的支柱性产业，经预测，2018～2021 年，我国钢产量、钢消费量、钢进口量、钢自给率均呈现平稳增长态势［1］。 高强钢薄板既有很高强度又有良好塑韧性，广泛应用于汽车行业、精密仪器、航空航天等工业领域［2-3］，因此高强钢薄板轧制的研究具有重要意义。

在高强钢薄板轧制过程中，轧机若出现剧烈振动，将造成轧件厚度不均、表面振痕等缺陷，甚至剧烈的瞬时振动可能会损坏轧机零部件，故深入研究轧机振动机理及预防振动的措施，已成为板带轧制相关课题的重要方向［3］。

轧机系统的输入和输出间关系复杂，一个输入量的变化可能造成多个输出量的变化，这种多参数间存在复杂耦合关系的不确定性系统很难用统一的振动理论来解释，被学术界称为“幽灵式”振动［4］。 钢铁企业在生产过程中积累了大量的实时监测数据（PDA 数据），其中蕴涵着包括轧机振动机理在内的设备运行客观规律，但这些数据量非常巨大，且其中参数与轧机振动间的关系非常复杂，传统数据处理方法很难处理如此庞大的数据，并从中挖掘出反映轧机振动客观规律的信息［5］。

深度置信网络（deep belief nets，DBN）算法是深度学习框架的一种，广泛用于数据分类和预测［6］。 误差反向传播（error back propagation，BP）算法，包括信号的正向传递和误差的反向传递，是深度学习的基础［7］，采用遗传算法（genetic algorithms，GA）优化BP神经网络，优化后的算法称为GA-BP 算法［8-9］。

本文将研究轧机振动的聚焦点放在PDA 数据上，采用DBN 算法和GA-BP 算法建立轧机振动预报模型，充分挖掘轧机PDA 数据，对轧机振动进行预报。通过现场实测数据训练本模型的精度，并应用本模型建立轧制工艺参数和轧机振动强度的定量关系，为轧制制度的改进以及在轧制过程中实现快速减弱甚至消除轧机振动提供建议。

1 热轧机振动机理分析

轧机的振动形式如表1 所示［10］，其中机架系统的垂直振动多为三倍频（指在150 ～250 Hz 内的低频振动），是高速板带轧制生产中危害性最大的振动［11］，因此，本文针对机架系统垂直振动的机理展开分析。

表1 轧机的振动形式

1.1 建立轧机垂直振动模型

研究轧机振动机理需要建立有效反映轧机振动的数学模型。 本文采用应用较为广泛的集中质量法建立轧机振动模型。 结合轧机特点及计算所需，将轧机系统进行简化，如图1 所示。 其中M1为机架立柱、上横梁、压下装置等的等效质量；M2、M5分别为上、下支撑辊系的等效质量；M3、M4分别为上、下工作辊系的等效质量；M6为下横梁、垫块等的等效质量；K1，C1以及K7，C7分别为上、下支撑辊的轴承座到上横梁支点的等效刚度和阻尼；K2，C2以及K6，C6分别为上、下支撑辊中部到轴承座的等效刚度和阻尼；K3，C3以及K5，C5分别为上、下工作辊和上支、下撑辊之间弹性压扁的接触刚度和阻尼；K4，C4分别为工作辊和轧件之间弹性压扁的接触刚度和阻尼。

图1 轧机垂直振动系统模型

1.2 计算轧机等效刚度和等效质量

轧机的基本参数如表2 所示。 若轧制过程中轧机发生振动，此时认为动能等于势能，将轧辊和机架看作梁，对其全长积分可得系统最大动能和势能。 即可求得系统各部分的等效质量和等效刚度［11］。

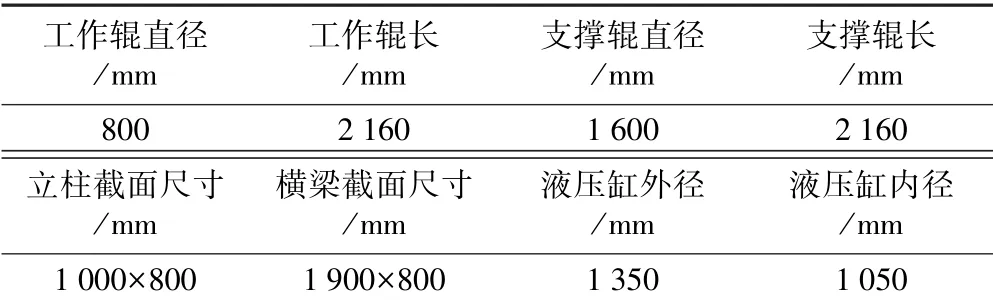
表2 轧机参数

按照能量守恒的原则，设Kx和Mx分别为梁上x点的等效刚度（N/m）和等效质量（kg），Vxm、Yxm分别为该点在振动过程中的最大速度（m/s）和最大位移（m），Txm为该点最大动能（J），ω为振动圆频率（rad/s），则等效刚度Kx和等效质量Mx为：

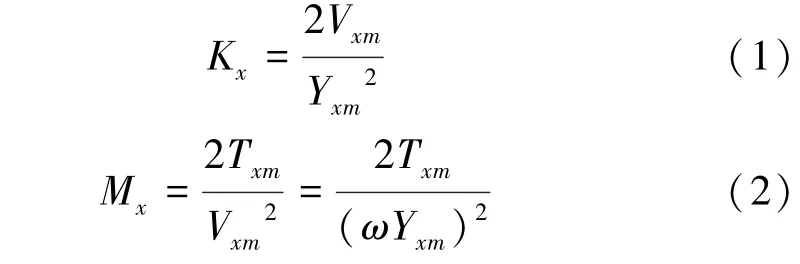
计算结果如表3 和表4 所示。

表3 等效刚度计算值/（GN·m-1）

表4 等效质量计算值/kg

1.3 求解轧机的固有频率和主振型

根据机械振动理论，经计算可知上述系统阻尼很小，可忽略阻尼对固有频率的影响。 对于六自由度的无阻尼系统，其矩阵形式的运动微分方程为：

式中［M］为质量矩阵；［K］为刚度矩阵；｛x″｝为等效质量的加速度列阵；｛x｝为等效质量的位移列阵。

求解上述系统振动固有频率与主振型，即为求解式（4）的特征值和特征向量：

式中［A］为主振型；p为圆频率，Hz。

根据计算出的等效刚度和等效质量，应用MATLAB进一步求解，求得该系统的各阶固有频率f1～f6见表5，图2 为该系统的各阶振型曲线。 由表5 和图2 可知，f3为159.14 Hz，从振动趋势上看，上下工作辊相反，上下支撑辊也相反，上下机架却相同，此时轧件厚度波动明显，且易发生自激振动，轧机振动最剧烈。

表5 F2 机架垂直振动固有频率计算值/Hz

图2 垂直振动各阶振型

用ICP 压电加速度计测量某钢厂F2 机架的垂直和水平振动，发现轧机在160 Hz 时垂直振动最剧烈，与本文计算求得的结果基本吻合，该频率位于3 倍频范围内，是高速板带轧制生产中危害性最大的振动。

2 轧机振动预报模型的设计

钢铁生产中各层级的数据存在多变量、非线性、强耦合的特点，传统的数据处理方法很难处理并从中挖掘出反映轧机振动客观规律的信息［5］。 DBN 算法通过多隐层人工神经网络，将高维数据转换为低维编码，能够有效降低数据间的相关度，提取出更加本质的数据特征，同时避免了维数灾难的出现，加快了运算速度［6］。 因此，本文采用DBN 算法对PDA 数据中特征进行挖掘、归类和降维，再将这些特征作为GA-BP 算法的输入，来预测轧机振动。

2.1 基于DBN 算法的设计

首先对所采集数据进行归一化处理，以方便处理数据中各个不同的参数；由于轧制工艺参数间存在很大的非线性，为提高预测精度，对采集数据进行聚类处理；由于轧机振动是一个多参数强耦合的复杂过程，因此需要用DBN 算法对数据样本进行降维处理，最终提取出更加本质的数据特征，进而作为GA-BP 算法的输入。

1） 原始数据的采集。 采集轧制相关数据，包括轧制力、轧制速度、入口厚度、压下率、入口张力、出口张力、轧件宽度、振动加速度，致振参数为轧制力、轧制速度、入口厚度、压下率、入口张力、出口张力、轧件宽度，将这些参数作为输入量，轧机振动加速度作为输出量。

2） 输入数据的归一化处理。 用premnmx 函数对原始输入数据归一化处理，即将原始数据的区间控制在［-1，1］之内：

式中P为原始输入数据；T为归一化数据；minp为P的最小值；maxp为P的最大值；minT为T的最小值；maxT为T的最大值。

3） 样本聚类处理。 聚类的计算步骤如图3 所示，聚类后对其有效性进行分析，以获得最佳的聚类数，本文采用DB 指标［11］，按式（6）计算：

式中k为聚类数量，初始化时设定kmin、kmax；Ui为Vi类全部离散数据至聚类中心的均值；Uj为Vj类全部离散数据至聚类中心的均值；Vij为Vi类和Vj类中心的均值。

图3 聚类计算步骤

4） DBN 算法降维处理。 根据DBN 算法原理［7］，经过反复调整和优化，本文降维处理步骤如表6 所示。

表6 降维处理步骤

2.2 DBN 算法提取数据特征的相关性分析

为了避免降维过程中数据特征的丢失，本文进行DBN 算法提取数据特征的相关性分析，采用Pearson相关系数法，用p表示，p的绝对值越大，相关性越强，如表7 所示。

对三类原始特征每一维特征进行相关性分析，结果如表8 所示。 第一类数据样本中，1～5 维中，随着维数升高，相关性越高，1 维、6 维和9 维为极弱相关或无相关，其他维都在中等程度相关及以上；第二类数据样本中，1～5 维中，随着维数升高，相关性越高，6 维和9维为无相关，1 维、2 维、7 维和8 维为弱相关，其他维都在中等程度相关及以上；第三类数据样本中，5～9 维为极弱相关或无相关，1 维和4 维为弱相关，2 维和3维为中等程度相关。

表7 相关性程度评价表

表8 三类原始特征相关性表

对第一隐层DBN 三类的每一维特征进行相关性分析，结果如表9 所示。 第一类数据样本中，1～2 维和5～8 维为无相关，其他维都在中等程度相关及以上；第二类数据样本中，所有维都为极弱相关或无相关；第三类数据样本中，1～8 维为无相关，9 维为弱相关。

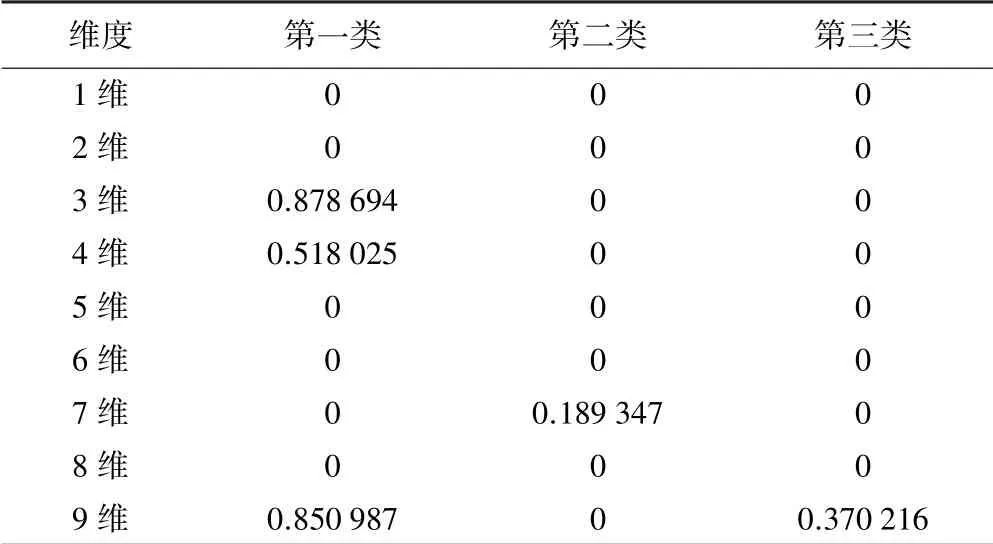
表9 第一隐层DBN 的特征相关性表

对第二隐层DBN 三类的每一维特征进行相关性分析，结果如表10 所示。 第一类数据样本中，3 维为弱相关，其他维都为极强相关；第二类数据样本中，所有维都为极弱相关或无相关；第三类数据样本中，所有维都为弱相关。

表10 第二隐层DBN 的特征相关性表

对第三隐层DBN 三类的每一维特征进行相关性分析，结果如表11 所示。 第一类数据样本中，1 维和3维为极强相关，2 维为强相关；第二类数据样本中，所有维都为极弱相关或无相关；第三类数据样本中，所有维都为弱相关。

表11 第三隐层DBN 的特征相关性表

对第四隐层DBN 三类的每一维特征进行相关性分析，结果如表12 所示。 第一类数据样本为强相关；第二类数据样本为极弱相关或无相关；第三类数据样本为弱相关。

表12 第四隐层DBN 的特征相关性表

通过以上分析，可知降维的维度并不与特征的相关性成比例，因此本文对降维后的所有特征用GA-BP算法预测，再将预测值融合，得到最终的预测值。

2.3 基于GA-BP 算法的设计

BP 神经网络的基本原理是信号向前传递，由输入层到隐层，经处理后再到输出层，如果未获得期望输出，则将误差信号传递回去，进行网络权值和阈值的修正和调整，以得到最优值，进而得到期望输出［8-9］。 由于BP 神经网络初始权值和阈值具有随机性，易陷入局部最优，映射速度慢，而遗传算法能弥补这一不足［8-9］，采用遗传算法优化BP 神经网络，由此得来GA-BP 算法。

1） GA-BP 神经网络参数初始化如图4 所示。

编码长度的计算公式为：

式中S为编码长度；R为输入层神经元个数；S1为隐层神经元个数；S2为输出神经元个数。

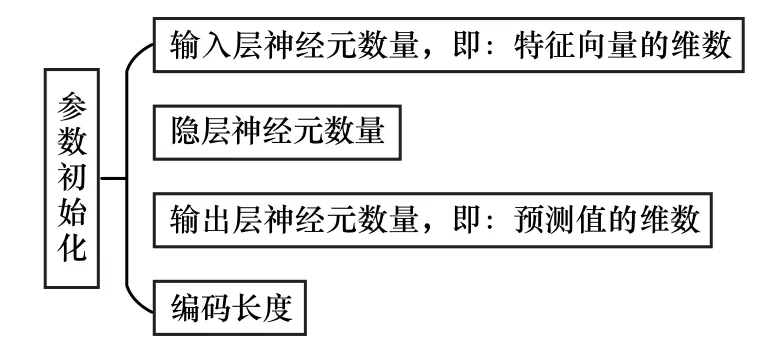
图4 GA-BP 神经网络参数初始化

2） 编码。 设置GA-BP 神经网络参数，计算权值和阈值数量，将权值和阈值编为一组，用相同数量的变量表示该组。 编码后的基因如下：

式中wij为输入层第j个神经元对隐层第i个神经元阈值；vij为隐层第j个神经元对输出层第i个神经元阈值；θi为隐层第i个神经元阈值；ti为输出层第i个神经元阈值。

3） 计算个体适应度值。 将振动加速度的预测值反归一化，再计算MSE 值。 反归一化计算公式为：

式中yi为第i个样本点归一化后的振动加速度；u为振动加速度的均值；σ为振动加速度的标准差；yi′为第i个样本点反归一化后的振动加速度。

4） 选择、交叉和变异。 以轮盘形式择优选取个体；再与上一代的优秀个体单点交叉，形成新的个体；为了防止算法出现“早熟”，并增强算法随机搜索能力，变动种群中个体的某一编码值。

5） 重复3），满足终止条件时，算法结束，得到最优网络的所有阈值和权值；反之重复4），继续迭代最优个体。 GA-BP 算法流程如图5 所示。

3 振动预报模型的应用分析

某厂于2005 年设计建造了热连轧生产线，其热轧带材设计年生产能力450 万吨。 主要产品有汽车结构用钢、桥梁用钢、船体结构用钢等。

该热连轧机在生产过程中，其F2 机架有剧烈的振动现象，在生产薄板坯时振动尤为严重，甚至导致轧机轧辊、分速箱齿轮出现了不同程度的磨损，对设备安全和产品质量产生了严重的影响。

该厂轧机轧制1.6 mm 高强钢薄板时振动明显，故采集了其轧制相关数据作为样本，共200 组原始数据，本文用其中100 组数据对本预报模型进行训练，以提高振动预报精度，利用另外100组数据进行预报，并分析预报误差，最后，建立轧制工艺参数和轧机振动强度的定量关系。

图5 GA-BP 算法流程

3.1 振动预报模型的训练

当前大多算法用最后一隐层的特征作为预测算法的输入，但这可能使特征在DBN 降维后陷入过拟合［11］，因此，利用预测值融合的方法来处理每一隐层的预测值，即对DBN 的3 个隐层降维后的特征都进行GA-BP 算法预测，再对预测值按式（10）进行计算，记为融合值，即最终的预测值。

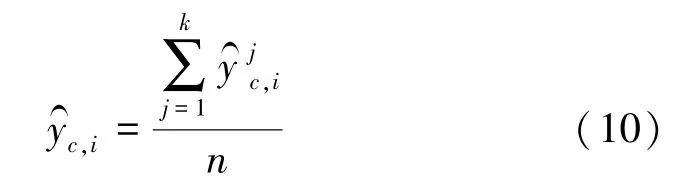
式中c为类别；i为样本编号；j为目标隐层；n为样本特征隐层个数；为c类中第i个样本的融合值；为c类中用第j个隐层的输出特征求得的第i个样本的预测值。

应用本预报模型预测后，与原始数据样本进行对比，根据对比结果来修正本预报模型，直至预报结果与原始数据的吻合度达到要求。 本模型训练后的最终预测结果如图6 所示。

通过预测结果可以看出，第一类预测结果中第一隐层接近实际振动情况，第三隐层与实际振动情况有较明显差距；对预测结果融合后，使预测结果接近实际振动情况。 在第二、第三类预测结果中三个隐层输出的预测结果都比较接近实际振动情况，预测结果较好。

3.2 预测结果的误差分析

图6 预测结果

为反映振动预报模型预测结果的准确性，结合现场实测原始数据，对预测结果进行误差分析，结果如表13 所示。

表13 预测误差表

对比结果表明，预测误差在3.94%以内，预测结果与轧机实际振动情况有较好的吻合度。

3.3 轧制工艺参数对轧机振动的影响

在高强钢薄板的轧制过程中，若轧机发生振动，传统做法大多是工人根据经验适当调整轧制工艺参数，以减弱轧机振动，这对工人经验水平有很高要求［5］。本文应用本振动预报模型分析轧制工艺参数对轧机振动的影响，以得出轧制工艺参数与轧机振动的定量关系，为优化轧制规程，以及在轧制过程中实现快速减弱甚至消除轧机振动提供更合理、更可靠的建议。

表14 是一组振动加速度为3.079 7g（g 为重力加速度）的样本数据，利用本文的振动预报模型，控制某一变量每次改变5%，保持其他变量不变，以探究各个轧制工艺参数与轧机振动间的定量关系，结果见图7。

表14 轧制工艺参数

图7 轧制相关参数变化影响轧机振动的预测结果

由图7 可见，随着轧制速度减小，轧机振动加速度不断减小，轧制速度减小20%时，轧机振动加速度减小1.63×10-3g；轧制速度增加10%时，轧机振动加速度增加1.10×10-3g。 随着轧制力减小，轧机振动加速度不断增大，轧制力减小20%时，轧机振动加速度增加2.01×10-3g；轧制力增加10%时，轧机振动加速度减小0.94×10-3g。 随着入口张力减小，轧机振动加速度不断增大，入口张力减小20%时，轧机振动加速度增加0.91×10-3g；入口张力增加10%时，轧机振动加速度减小0.49×10-3g。 随着出口张力减小，轧机振动加速度不断减小，出口张力减小20%时，轧机振动加速度减小2.76×10-3g；出口张力增加10%时，轧机振动加速度增加2.11×10-3g。 轧机振动加速度与轧件宽度之间没有明确的变化规律，轧件宽度从1 100 mm 变化到1 700 mm 的过程中，轧机振动加速度最大值和最小值的差值为1.40×10-3g。 随着入口厚度减小，轧机振动加速度不断增加，入口厚度减小20%时，轧机振动加速度增加0.70×10-3g；入口厚度增加10%时，轧机振动加速度减小1.1×10-3g。 随着压下率减小，轧机振动加速度不断减小，压下率减小20%时，轧机振动加速度减小1.50×10-3g；压下率增加10%时，轧机振动加速度增加0.80×10-3g。

将除轧件宽度外的6 个变量对轧机振动的影响统一观察，结果如图8 所示。 发现轧制速度、轧制力、出口张力、压下率对振动加速度的影响相对较大，入口张力和入口厚度对振动加速度的影响相对较小。

4 结 论

1） 针对某钢厂F2 机架，建立了轧机垂直振动模型，计算其各阶固有频率和主振型，发现第三阶固有频率最容易引起轧机自激振动，轧机振动最为强烈，模型预测结果与实际振动情况相符。

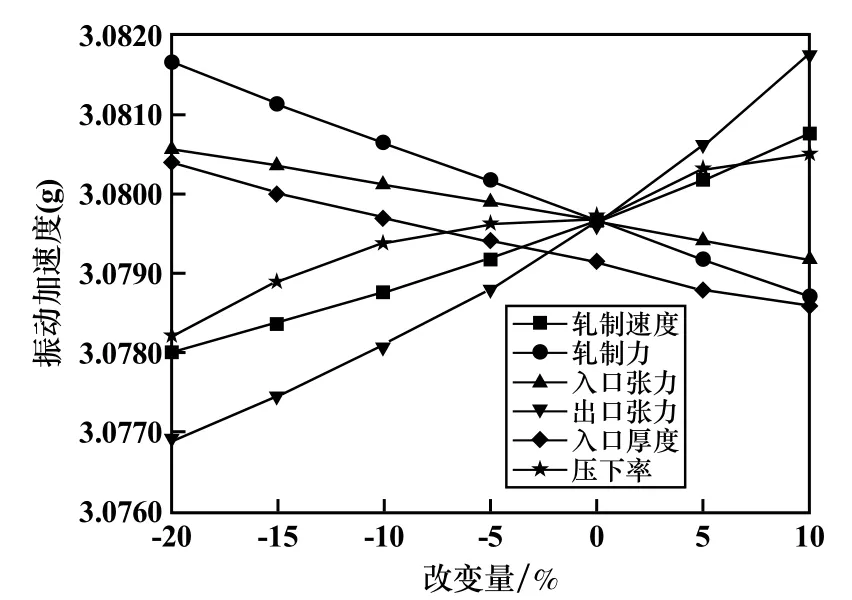
图8 6 个变量对轧机振动影响的预测结果

2） 应用DBN 算法和GA-BP 算法建立轧机振动预报模型，对PDA 数据进行分析和挖掘，并利用预测值融合的方法，防止特征在DBN 算法降维后陷入过拟合。 训练本预报模型，对预测结果进行误差分析，误差在3.94%以内，证明本预报模型计算精度较高，可用于轧机振动的预报。

3） 应用本振动预测模型，定量分析了轧制工艺参数的变化对轧机振动的影响，为优化轧制规程，以及在轧制过程中实现快速减弱甚至消除轧机振动提供更合理、更可靠的建议。