露天矿三维境界参数优化与应用①

曾凌方

（长沙有色冶金设计研究院有限公司，湖南 长沙410011）

露天境界优化及选择是露天矿山设计及生产的基础，它确定矿山生产期内的开采矿量、出矿品位、服务年限、生产成本及效益等主要经济技术指标，也影响矿山的长远发展规划。 而露天境界优化中经济参数的选取至关重要，它影响最优露天境界的确定。

20 世纪60 年代初，美国勒奇（Lerch）和格罗斯曼（Grossman）首次运用动态规划法和图论法圈定露天矿境界。 20 世纪80 年代中期大量计算机辅助下的运筹学方法开始广泛应用于生产实践。 主要优化算法有浮动圆锥法、图论法、网络最大流法、线性规划法等［1-3］，其算法基础都为矿床地质块段模型，运用地质统计学对矿体品位进行估值，并将经济价值和生产成本等参数赋值于矿岩块，计算块的价值，判别其是否存在开采价值。 但所赋经济参数多为当前形势下的取值，且均未考虑资金的时间价值，另外境界的几何约束也多为经简单类比或简单数值分析获得的非确定参数。 20世纪80 年代末，国内外部分学者开始认识到这一问题，并提出解决方案［4-5］。

本文尝试通过经济时间序列和神经网络方法对境界优化中的经济参数进行预测，利用编制的生产进度计划实现模型中块参数赋值，经境界优化及净现值比选，确定最优终了境界。

1 境界优化技术路线

露天矿开采境界综合优化方法实现的技术路线如图1 所示，主要包括3 个阶段：矿床基础模型创建、参数估值预测及境界优化研究。

图1 露天矿三维设计方法技术路线

1.1 基础模型创建

矿山基础模型是依据有关的测量、勘探、化验等数据信息资料，运用矿业三维软件平台建立一体化三维模型，主要包括矿区地表模型、矿体模型、岩性模型、构造模型及块体模型等［6］。 矿区地表模型是将赋有高程的等高线导入Surpac 软件形成三维地表模型。 矿体模型、岩性模型、构造模型是根据地质勘探工程圈定的矿体轮廓线、岩性分界面、构造边界线，以三维手段描述各自的空间分布状态而建立的实体模型。 块体模型以实体模型为基础，按照钻孔、探槽及坑探等化验数据，将各种基础属性赋值于各个块体中，同时定义块体的基础块尺寸、次级块尺寸等，这是境界优化的基础工作。

1.2 参数预测及赋值

首先采用变异函数模型分别沿矿体走向、倾向、倾角三个方向进行变异函数分析，在确定理论变异函数的主要参数后，利用Surpac 软件对矿石进行品位估值，建立符合地质报告中资源储量的三维矿体模型。该法充分借助计算机技术，不仅提高建模效率和估算精度，同时降低传统计算方法对矿体形态和探矿工程的依赖程度，且能够通过实体模型确定矿体在三维空间中的分布，实现了计算结果的三维可视化。 另外还可通过创建属性文件对任意块属性赋值，如块的矿石类型、岩性、比重、储量级别等参数。 建立贴合实际块模型是境界优化的基础，同时也是指导以后生产的依据。

时间序列分析是一种定量的回归预测方法，其原理是承认事物发展的持续性，运用过去的时间序列数据进行统计、分析及处理，消除随机偶然因素及随机波动产生的影响，推测出将来事物的发展趋势及发展规律［7-8］。 首先获取大量历史数据，通过对序列的自相关和偏相关特性分析，确定预测模型类别，经参数估算后形成预测模型，在此基础上可进行一定幅度的外推预测，如矿产品售价、开采成本、边坡角［9］。 计算公式为：

式中yt为时间序列；θ 为平均移动系数；φ 为回归系数；ut为相互独立的白噪声序列；n 为样本数；k 为滞后期；为样本算术平均值；rk为自相关系数；φkk为偏自相关系数；（l）为预测值。

神经网络系统是一种高度自适应的非线性动力学系统，可通过大量样本的学习来抽取隐含在样本中的因果关系，擅长处理随机的、包含众多因素的非线性问题，故特别适用于复杂边坡等岩体工程失稳灾害这种非线性动力学问题。 神经网络主要包括输入层、隐含层及输出层，输入层各神经元负责输入信息，并把信息传递到隐含层神经元；隐含层是信息处理层，负责信息处理交换；输出层负责输出各神经元的信息。

1.3 境界优化原理及过程

公式（5）是L-G 法获得露天境界内的矿块总价值：

式中vi为单个矿块体积；ρi为矿块密度；βi为单个矿块品位；po为矿产品售价。 通过对矿产品售价折扣方式可获得系列境界方案。

根据矿山地形、总图布置、生产能力及采剥发展顺序，利用MineSched 进度计划编排软件对各境界矿岩量进行排产，从而获得各方案的矿岩采剥总量、剥离量、基建工程量、出矿品位等数据，由此可进行年采剥费用、基建投资、年收益等计算，通过计算各方案NPV进行优化选择。 公式（6）是各境界方案的NPV计算公式：

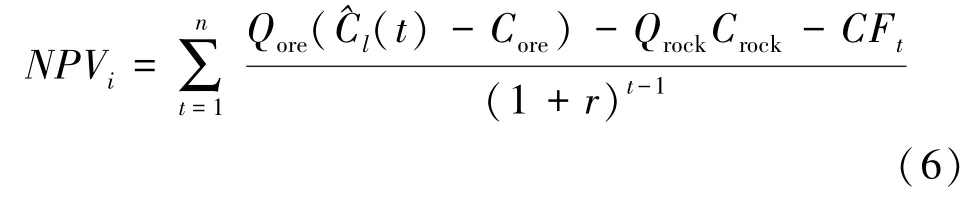
式中NPVi为第i个采剥方案的净现值；^Cl（t）为预测未来第t年的售价；Qore为第t年开采的矿石量；Qrock为第t年开采的剥离量；Core为第t年矿石生产成本；Crock为第t年剥离成本；r为贴现率；CFt为第t年投资额。

2 应用实例分析

2.1 矿山概况

某矿为内蒙古卓资县一大型斑岩型钼矿床，矿石类型为辉钼矿石。 矿区工程地质、水文地质及开采技术条件简单，矿体埋藏浅，适于露天采矿。 根据矿山地形地质图、钻探数据、勘探线剖面图及岩层信息等数据，创建了矿山实体模型。 图2 为矿山地表及矿体实体模型，矿体由两个主矿体构成，分别为Ⅰ矿体和Ⅱ矿体。

图2 矿床实体模型

2.2 优化参数预测及批量境界生成

结合露天开采工艺及勘探网度等因素，确定块体尺寸为10 m ×10 m ×5 m，可分解次级块尺寸为5 m ×5 m × 1.25 m。 依据变异函数参数设定了克立格估计参数和球状变异函数模型参数，对钼品位进行估值。图3 是品位估值后的矿床块体模型，估值信息主要包括矿体品位、矿岩密度、资源储量级别和矿石类型等。

收集国内类似岩性的20 个已生产矿山边坡参数作为样本库，取岩石容重、抗压强度、抗拉强度、岩体内聚力、地下水影响、边坡高度、结构面状况、爆破震动、岩体弹性模量共9 个对边坡稳定性影响较大的因素作为网络预测模型的基础数据，建立三层网络模型，其中输入层9 个神经元，隐含层6 个神经元，输出层3 个神经元。结合矿区组成边坡岩性的节理裂隙发育、岩层产状、岩性及构造分布，将矿区边坡分为3 个区域，取各区典型剖面进行分析，将参数输入预测模型，获得3组边坡角参数，见表1。

图3 矿床块体模型

表1 境界优化参数

取2013～2018 年钼精矿销售价格为分析对象，通过对钼价时间序列自、偏相关性分析，创建了ARIMA（2，1，2）预测模型，采用动态法外推预测。 预测结果显示，钼精矿价格总体呈上升趋势，在2015 年出现低谷后，价格有小幅度上升，随后基本处于小幅度震荡状态，未来5 年钼精矿平均售价在1 500 ～1 800 元/t。 以同样方式分析了矿山采选及剥离等成本，详细参数见表1。

矿石采矿损失率2.5%（回采率97.5%）、选矿回收率88%、贴现率12%，根据表1 优化参数，利用L-G 图论法，以5%的矿石售价折扣对露天境界进行优化，获得了-35、-30、-25、-20、-15、-10、-5、0、5、10、15、20、25、30、35 共15 个境界坑方案，分别命名为Pit1、Pit2、Pit3、…、Pit15。 图4 为境界优化生产的批量境界。

图4 露天矿批量境界

2.3 境界方案的动态分析

通过境界优化可知，矿区西部Ⅰ矿体品位较高，上部剥离少，选为矿山首采区，根据露天采场与选厂、排土场位置关系，将露天采场出入沟口布置在两坑之间靠近西境界的北部，采剥由北往南推进。 在保证二级矿量的前提下，尽量降低并平衡前期剥采比。 根据预选设备确定工作面宽度不小于40 m，工作线长度不小于150 m，台阶高度15 m。 利用MineSched 软件，根据上述原则对各境界方案编排生产进度计划。 根据进度计划结果可获得矿山基建工程量、年矿岩采剥总量、年出矿品位等信息。 由基建工程量计算基建期投资，根据矿山年矿岩采剥量及服务年限可进行设备投资估算，根据出矿品位、采出矿量及金属售价、废石剥离量等信息，按公式（2）计算各方案净现值。 图5 为折现率取12%时各方案净现值及平均剥采比折线图。 由图可知Pit9 方案（矿产品售价为原售价的1.05 倍）处的平衡剥采比发生跳跃且净现值最大，从矿山投资角度来看，此时的境界可使企业获得最大的经济效益。

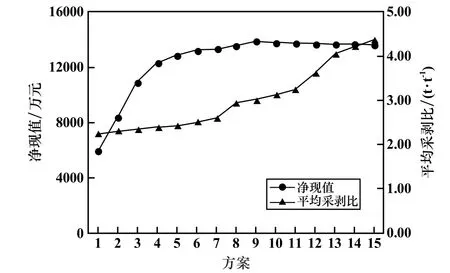
图5 净现值及剥采比

在最终境界DTM 模型基础上以15 m 高差提取台阶等值线，根据边坡组成的几何约束参数采用线文件扩展及人工绘制相结合的方式形成如图6 所示的终了露天境界三维图。

3 结 论

1） 矿山开采境界对矿石品位、产品销售价格、边坡角等经济参数有着很强的敏感性，将时间序列及神经网络方法引入境界优化过程，实现了经济参数及边坡角的科学预测，在此基础上获得最佳终了境界。

2） 三维境界优化涉及多种复杂信息，基于经济参数的预测能够较为精确地确定各种数据，以减少人为主观判别、数据收集和整理过程的误差，为后续境界优化中参数输入提供数据支撑。

图6 终了露天境界三维图

3） 计算机辅助下的露天三维境界优化，可视化程度高、运算速度快、操作灵活、精度高，可根据需要实时调整经济模型及相对应的数据库，短时间内完成多套开采方案比选，提高工作效率。

4） 该方法应用于某钼矿山表明：利用境界动态优化所得最优境界方案9 净现值较图论法直接获得的无折扣境界方案高出1.21 亿元，因此，三维动态优化方法可使矿山企业获得更好的经济效益。