基于多目标分解策略的副本布局算法研究*
邵必林,贺金能,边根庆
1.西安建筑科技大学管理学院,西安 710055
2.西安建筑科技大学信息与控制工程学院,西安 710055
1 引言
随着大数据和云计算的飞速发展,数据存储作为其中关键性的一个环节也备受关注[1]。鉴于时代背景和运用场景发生巨大转变,传统的存储技术已经逐渐不适用于云计算下分布式的环境,海量的数据、异构的环境、高可靠性以及可用性需求都超出了传统存储技术的处理范围,迫切需要新的技术方能满足目前现状的需求。由于同时具备加快访问速度、提高可用性和可靠性等提升存储系统效能的作用,副本技术已经逐渐成为研究的热点。
为了在分布式存储系统中有效地发挥副本技术的优势,有两个关键性的问题亟待解决:第一个问题是为每一个数据选取多少个副本是合适的;第二个问题是如何放置这些副本来满足系统效能的要求。把这两个相关联的问题合称为副本的布局问题。
研究人员针对这两个问题展开了很多研究[2-9]。目前现有的副本布局策略大都是研究副本带来的收益,比如高可靠性、高访问效率、负载均衡等,但是没有考虑到副本的创建和维护需要消耗系统资源。一方面要使用更多的副本来提高系统的效能,另一方面又要削减副本的数量来减少能量消耗,因此需要一个合理的副本布局策略平衡上述矛盾。当前的副本策略在考虑副本布局问题时也没有把数据中心的能量消耗作为一个主要的优化目标,只是单纯优化少部分效能指标。目前数据中心能耗问题越来越突出,提出一种兼顾数据中心能耗的数据副本布局方案就显得刻不容缓。
综合上述问题,本文将基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition,MOEA/D)[10]运用于求解副本布局的多目标优化问题上,提出了一种基于多目标分解策略的副本布局算法(replica layout algorithm based on a multi-objective decomposition strategy,MDSRL),将平均文件不可用性、负载均衡、能量消耗作为三个优化对象综合进行考虑,试图找到合适的副本数和副本放置方案。MDSRL把这三个目标分解成多个标量子问题同时进行优化来得到一组折衷解,得到的解在三个目标上都能取得比较不错的表现。
本文的主要贡献如下:
(1)构建了文件可用性、负载均衡以及能量消耗三个目标的目标函数并建立了多目标函数模型。
(2)设置了一种新的性能度量指标超体积占比(hypervolume account,HVA),以度量不同算法所得的一组折衷解在收敛性和分布性上的优劣情况。
(3)提出了一种基于多目标分解策略的副本布局算法MDSRL,寻找到了一组在平均文件不可用性、负载均衡以及能量消耗上都有良好表现的折衷解,并且解的分布性和收敛性较好。
2 相关工作
副本技术在万维网、P2P(peer to peer)系统、分布式系统以及云存储系统中得到了广泛的应用[11-12],甚至在物联网中也逐渐被使用[13]。因此副本布局的研究被越来越多的学者所重视[14-15]。
关于副本数量的选择问题,已有许多学者对其进行了深入的研究。目前现有的分布式文件系统采用的副本个数一般是固定的三个,这样会导致需要更多的副本时达不到可用性需求,只需要较少副本时又会白白消耗系统能量。陶永才等[2]提出了一种动态副本管理机制(dynamic replica management scheme,DRM),在满足可用性要求的情况下最小化副本数目。李帅等[3]提出了一种基于多访问策略的副本动态更新算法(min-placement far servers first,MPFSF),通过对通信距离设置阈值来判断是否增加和删除副本。Qu等[4]提出了一种基于改进马尔科夫模型的动态副本管理策略(dynamic replica strategy based on improved Markov model,DRS),通过改进的马尔科夫模型对冷热数据进行分类,根据分类结果决定是否增加和减少副本个数。但是上述策略都没有考虑如何平衡副本带来的系统开销和效能之间的矛盾。
云计算环境分布式存储的副本放置问题是一个NP难问题。由于进化算法(evolutionary algorithm,EA)可以同时在搜索空间搜索多个解,因此很适合求解NP难问题,研究者们尝试使用进化算法来选择最合适的副本放置位置方案。Cui等[5]提出了基于蚁群算法的副本放置策略,通过遗传算子不断迭代来找到最合适的数据节点,实验证明该策略减少了数据传输费用。罗四维等[6]提出了一种免疫优化策略的副本放置算法,通过克隆选择算子和记忆机制能够选择更加合适的副本放置节点,从而达到降低副本访问开销的目的。虽然已有的这些副本策略都在一定程度上优化了系统的效能,但是针对的大都是单个目标,并且只是单方面提高系统的效能,没有从全局的角度考虑副本所带来的能耗问题。
Hassan等[7]提出多目标进化算法(multi-objective evolutionary,MOE),将访问延迟、存储费用以及系统可靠性作为三个要优化的目标,并用快速非支配排序遗传算法(nondominated sorting genetic algorithm II,NSGA-II)[8]寻找一组折衷解,不过该算法没有考虑到能耗和负载均衡两个关键的指标。Long等[9]提出了一种多目标优化的副本管理(multi-objective optimized replication management,MORM)算法,基于人工免疫算法对平均文件不可用性、服务时间、负载均衡、能耗以及延迟五个目标进行了优化,但只是单纯将五个目标函数进行线性加权,将多目标转化为单目标进行求解,方法容易实现但是很难对解的优劣性进行客观评价。
综合前人工作的不足之处,本文将分解策略引入副本布局问题的多目标优化中,提出了MDSRL算法。文件可用是副本技术的首要目标,负载是否均衡将影响到系统的可靠性、稳定性、吞吐量以及响应时间,能耗问题在存储系统中变得越来越突出,因此综合考虑了平均文件不可用性、负载均衡和能耗三个目标。分解策略能够将这三个目标分解成多个子问题同时进行优化,借助领域内若干子问题提供的信息能够快速找到一组在三个目标上表现良好且分布性和收敛性较好的折衷解,并且实验证明了MDSRL算法能够动态调整副本的个数,有效平衡了副本开销和效能之间的矛盾。
相比于目前最优的多目标优化算法MOE,本文所提出的算法考虑到了负载均衡和能耗两个关键性指标,并且本文所提出的算法在平均文件不可用性和能耗上能取得比MOE算法更好的表现,同时MDSRL得到的折衷解在分布性和收敛性上比MOE更好;相比于当前优化目标个数最多的副本布局算法MORM,MDSRL并没有优化五个目标,但是MDSRL在平均文件不可用性和负载均衡上比MORM取得更好的表现,同时在能耗问题上的表现随着文件个数增多以后也能超过MORM,并且MORM不能得到一组折衷解,在某些目标上的较大提升是以在其他目标上的下降为代价,而MDSRL却能得到一组折衷解。
综上所述,本文所提出的算法在平均文件不可用性、负载均衡、能耗上都取得了相对不错的表现,并且本文提出了一种新的折衷解的性能度量指标方式,证明了本文所提出的算法比其他算法得到的折衷解在分布性和收敛性上更好。
3 系统模型和优化目标
3.1 问题定义
在云存储系统的分布式集群中,假设有m个数据节点D1,D2,…,Dj,…,Dm,有n个文件F1,F2,…,Fi,…,Fn,需要存储到这些数据节点上,副本布局策略就是将这n个文件合理部署到m个数据节点上,以使设定目标函数的效能达到最优。
根据上述对副本问题的定义,提出了基于多目标分解策略的副本布局算法MDSRL,为不失一般性,现针对云存储系统中的分布式场景做出如下假设:
(1)为了简化问题,除了第一次写入文件之后,后续对文件的访问是“只读”操作,并且对文件的每次访问都是顺序读取的,不考虑其他访问的形式。
(2)m个数据节点都是相互独立且异构的,节点存储副本和请求访问副本都是依赖于数据节点性能的,数据节点本身的性能指标对于副本放置位置的选择有着约束的作用。
(3)把文件作为一个整体考虑,但是对于更细的粒度比如文件块,可以把每一个文件块视作一个单独的文件进行处理,本文所提出的算法仍具有适用性。
3.2 多目标优化模型
副本的多目标优化问题可以由式(1)的数学模型所表示:

设Ω表示一个个体,Ω(i,j)为决策变量,在云存储系统中,每个个体都表示n个文件的副本分配到m个数据节点的一种分配方案,因此每个个体都构成了一个n×m阶的矩阵,矩阵中的每个值采用二进制的形式来表示,Ω(i,j)的值为1表示第i(i=1,2,…,n)个文件的副本存储到了第j(j=1,2,…,m)个数据节点上,值为0表示未存储。表1描述了个体的一个样例。每一行表示了一个文件在不同数据节点之间的副本布局策略,每一行的和表示该行所代表的一个文件的副本因子。

Table 1 Binary representation of individual表1 个体的二进制表示
当一个个体满足以下两个约束条件(可行域)时称之为可行解。
(2)每一个数据节点上所有文件的大小之和必须小于该数据节点的总容量,即对于∀j∈{1,2,…,m},都有,其中CPj表示数据节点的容量。
因此,当一个个体只要不满足上述约束条件的任意一个(不在可行域内),该个体便是不可行解。
3.3 优化目标
多目标优化问题(multi-objective optimization problems,MOP)和单目标优化问题(single-objective optimization problem,SOP)的不同在于多目标优化往往得不到满足所有目标函数的全局最优解,因为目标之间可能存在相互冲突[16],比如为了最小化文件不可用性需要创建更多的副本,但是更多副本数又会增加系统的能耗,与最小化系统能耗的目标相矛盾。因此,本文试图通过求得一组折衷的解来平衡冲突的目标,从而得到在各个目标上都表现良好的折衷方案。多目标优化所得的解是根据待优化目标的函数值来不断迭代演化得到的,因此待优化目标的目标函数表示决定了进化的方向。下面将详细给出平均文件不可用性(mean file unavailability,MFU)、负载均衡(load variance,LV)、能耗(energy consumption,EC)三个目标函数的表示。
3.3.1 平均文件不可用性(MFU)
文件的可用性要考虑到数据节点的失效率以及该数据节点的链路失效率。Ω(i,j)为决策变量,当文件Fi放置到数据节点Dj上时,令Ω(i,j)等于1,否则为0,设pj为数据节点Nj(1 ≤j≤m)发生故障的概率,设μj为数据节点Dj(1 ≤j≤m)连接的链路出现故障的概率,设数据节点和所连接链路的故障率初始时是随机生成的。某个文件的一个副本不可用的情形是该副本所在数据节点出现故障或者连接该数据节点的链路发生故障。由于每个文件都有相应的副本,并且每个副本都分布于不同的数据节点上,因此某个文件不可用当且仅当这一文件的所有副本都不可用。因为每个副本都是独立同分布的,文件Fi不可用性可以由式(2)计算:

其中,∏*表示为非零元素(即Fi存在于数据节点Dj上)的累积乘。
一个系统数据可用是当且仅当所有的文件都可用,而文件可用性P(Fi)可由得到。因此系统数据可用性(system availability,SA)的计算如式(3)所示:
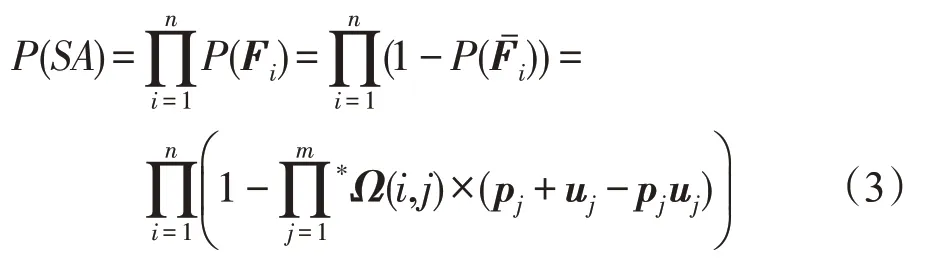
为了和多目标优化问题中大多数优化目标保持一致的优化方向,最大化系统可用性可以转化为最小化平均文件不可用性。因此,平均文件不可用性的目标函数MFU的计算如式(4)所示:

3.3.2 负载变化(LV)
负载均衡能够由负载变化来度量。由于标准差能够衡量数据的离散程度并与数据的量纲一致,因此数据节点的负载变化可以用负载的标准差来表示,并作为衡量系统负载均衡的标准。负载的标准差值越小,表明负载均衡能力越强,根据文献[17],数据节点Dj上文件Fi的负载L(i,j)值等于其访问速率和服务时间的乘积[17],因此L(i,j)可以由式(5)计算而得:

其中,V(i,j)是访问数据节点Dj时对文件Fi读请求的访问速率。如果该数据节点上不存在文件Fi,则让V(i,j)=0。ST(i,j)为文件Fi在数据节点Dj上的服务时间,其计算方法如式(6)所示:

其中,Si是文件Fi的大小,TSj是数据节点Dj的传输速率。
数据节点Dj的负载可以由在其上所有文件的负载之和得到,如式(7)所示:

那么,系统的平均负载就可进一步表示为式(8):

负载变化目标函数LV可以由标准差计算公式得到,如式(9)所示:
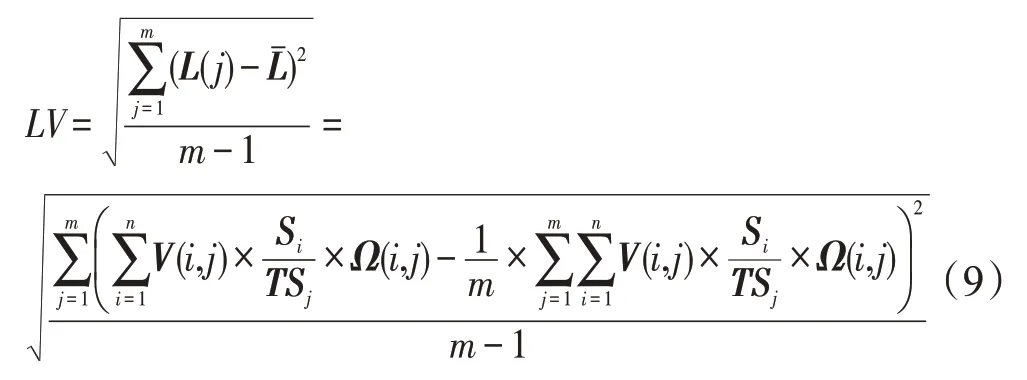
3.3.3 能耗(EC)
可再生能耗(renewable energy consumption,RE)和制冷能耗(cooling energy consumption,CE)占据系统总能耗的很大一部分,其他的部分可以忽略不计[18]。因此为了在最大程度上缩减能耗,就必须最小化RE和CE。文献[19]表明,服务器的能耗能够通过功率消耗和使用率之间的近似线性关系来进行较高准确率的度量[19]。本文使用了文献[9]中比较不同类型服务器的功耗图,它通过服务器端的Java程序分别测得系统CPU负载从10%到100%的功耗,图1中描述了本文中数据节点所使用的不同服务器的功耗随着负载率变化的曲线。

Fig.1 Power consumption by selected servers at different load levels图1 服务器在不同级别的功耗
负载率的计算如式(10)所示:

式中,L*(j)是数据节点Dj上的峰值负载,其实际负载率可以由转化为目前在Dj上所有文件的容量在整个节点的容量占比来进行计算,如式(11)所示:

设ERE(j)为数据节点Dj的计算机设备所消耗的可再生能源。ERE(j)的计算如式(12)所示:

其中,Pmax(j)表示数据节点Dj在处于负载率为100%时所消耗的功率,而Pidle(j)表示数据节点Dj处于负载率为0时所消耗的功率。因此,系统中数据节点所消耗的总功率如式(13)所示:

系统的能耗有一部分会转化为热能。设Γ表示数据节点的性能系数(coefficient of performance,COP)。COP越高,表示数据节点的冷却系统效率更高。COP主要取决于室内和室外的温度两个因素(Tin和Tout)。Γ的计算如式(14)所示:

在本文中,设Tout=36,Tin=26。设ECE(j)表示数据节点Nj的制冷能耗,那么有:

每个数据节点的制冷能耗之和就是系统总的制冷能耗。因此,总的制冷能耗可以用式(16)表示:

那么,系统总的能耗(system energy consumption,SEC)就由系统总的可再生能耗和总的制冷能耗之和所表示,可以由式(17)计算而得:

因此,能耗目标函数EC可用式(18)表示:
4 基于多目标分解策略的副本布局算法
4.1 基本定义
定义1一个多目标优化问题可以描述如下:

这里Ω是决策空间,F:Ω→Rt包含t个实值目标函数,Rt被称为目标空间。可实现的目标集合被定义为{F(x)|x∈Ω}。
定义2对于最小化多目标问题,对于n个目标分量fi(x),i=1~n,任意给定两个决策变量xa、xb,如果有以下两个条件成立,则称xa支配xb,表示为xa≺xb。
(1)对于∀i∈{1,2,…,n},都有fi(xa)≤fi(xb)成立。
(2)∃i∈{1,2,…,n},使得fi(xa)<fi(xb)成立。
如果对于一个决策变量x*∈Ω是Pareto最优解,当且仅当不存在决策变量x∈Ω使得x≺x*。Pareto最优解集是所有Pareto最优解的集合,帕累托前沿指的是Pareto最优解集对应的目标函数值的向量空间。
定义3切比雪夫数学模型如下:

z*=是参考点,对于任意i=1,2,…,t,,对于每一个Pareto最优解x*就存在一个权重向量λ使得其为此问题的最优解,因此通过改变权重向量就能获得不同的Pareto最优解。
定义4设解集X是Pareto前沿面的近似解集,是目标空间的一个参考点,对于任意i=1,2,…,t,,它被解集X中所有目标向量支配。那么关于参考点r*的超体积(hypervolume,HV)指的是被解集X所支配且以参考点r*为边界的目标空间的体积,如式(21)所示:

超体积能够在某种程度上综合反映解集的收敛性和多样性,HV值越大表明生成的解越好。用超体积的量化指标能够看到在一种算法上生成解集的好坏。因为不同的算法生成的解集是不同的,所以r*不同将导致在不同方法上生成的解集无法进行优劣性比较。因此本文将结合切比雪夫方法中的参考点z*来进行综合评判,新的度量指标超体积占比HVA的计算如式(22)所示:

HV(X,z*)是关于参考点z*的HV,HVA指的是解集X关于参考点r*的HV值占其关于参考点z*和r*的HV值之和的比例,HVA越大,说明解集X越好。
定义5根据种群个数N,MDSRL将多目标优化问题分解为N个子问题,同时生成N组均匀分布的权重向量,一个权重向量的邻域被定义为离它最近的几个权重向量的集合,通过邻域的信息来更新权重向量获得不同的Pareto最优解。通过切比雪夫模型能够将Pareto近似的子问题转化为标量子问题,不断逼近参考点来获得更好的Pareto最优解。
4.2 算法流程
MDSRL的算法结构是基于MOEA/D算法的,下面是算法的详细过程:
算法1MDSRL

步骤1在第1代时,先随机生成N个个体作为初始的种群P。由于个体是随机创建的,它可能不满足之前所定义的容量约束和完整性约束条件,因此要进行可行性检查和做相应的修复来满足约束条件,使得所有产生的个体都是可行解。同时要产生一组均匀分布的权重向量代表各个子问题的进化方向。
步骤2根据每个个体权重向量之间欧氏距离的大小来选取最近的T个个体作为邻域,把初始种群中个体在三个目标函数上的最小值作为参考点Z*,最大值作为参考点R*。
步骤3从邻域中随机选择两个个体K、L并使用遗传算子交叉和变异操作进行处理,对交叉变异后的子代进行可行性检查,修复不可行的个体,利用子代中的两个个体与Z*和R*中的函数值比较,更新Z*和R*,然后在子代中找出非支配解β。
步骤4采用切比雪夫方法使得个体不断向着参考点Z*逼近,使得解不断向着最优的方向进化。同时将每次得到非支配解β与外部种群中的解进行比较,从EP中移除所有被β支配的解,如果EP中的向量都不支配β,那么将β加入到EP中。
步骤5遍历种群中的个体,不断更新邻域解、Z*、R*以及EP的值。
步骤6若gen≤G,则gen=gen+1,把步骤4中得到的种群作为新的种群,然后转步骤3;否则达到停止条件,算法结束。
4.3 MDSRL的时间复杂度分析
对于给定的数据节点集D={D1,D2,…,Dj,…,Dm},文件集F={F1,F2,…,Fi,…,Fn},设初始种群中的个体数为N,最大代数为G,生成初始种群共花费了O(Nn+Nm)的时间复杂度,寻找相邻的若干个个体的时间复杂度花费为O(N2),寻找参考点Z*和R*用了O(N)的时间,交叉变异操作花费了O(mn)的时间复杂度,更新领域解花费了2O(3T)的时间复杂度,更新EP花费了O(N)的时间复杂度,由于遗传代数为G,因此MDSRL算法的最坏时间复杂度为O(Nn+Nm)+O(N2)+O(N)+(O(mn)+2O(3T)+O(N))NG=O(GN2+GNmn+GNT+N(m+n)+N2)。由于G、N、T都是事先配置的常量,不算在时间的复杂度中,因此MDSRL的最坏时间复杂度为O(mn)。
5 模拟实验和分析
为了模拟和验证本文所提出基于多目标分解策略的副本放置算法MDSRL的有效性,本章完成了一系列的模拟实验,利用Python3对该算法进行了实现和验证,处理器为Intel®CoreTMi5-7400M@3 GHz,内存为8 GB DDR4 SDRAM,硬盘为128 GB SSD,操作系统是Windows 10/64 bit。
5.1 实验参数设置
表2描述了实验中所采用的数据节点的配置参数。根据Long等[9]的工作,本文模拟了文件在8个数据节点之间的指派问题。提出的MDSRL算法中使用到的参数值如表3所示。在模拟实验中,由于假设的是“只读”操作,因此不用考虑数据的一致性怎么维护以及写操作所带来的开销。为了能够更好模拟云系统的访问行为,根据Xie等[20]提出的伪负载生成器建立一个符合文件访问规律的负载生成器,能够生成文件和请求。

Table 2 Data node configurations表2 数据节点配置

Table 3 MDSRL configurations表3 MDSRL的配置
5.2 实验结果分析
本文的实验是用MDSRL算法解决分布式存储系统中副本的多目标优化问题,同时和前面提到的MOE和MORM算法进行对比,图2展示了这三个算法的最后一代个体在MFU-LV-EC三维空间坐标上的分布图。

Fig.2 MFU-LV-EC objective space图2 MFU-LV-EC目标空间
从图2中可以发现MDSRL和MOE都能够生成一组折衷解,但是MORM只能生成一个最优解,这是因为MORM将多目标优化转化为了单目标优化,但是单目标优化通常只会产生单个最优解,而MDSRL采用的MOEA/D和MOE采用的NSGA-II都是多目标进化算法,因此能够得到一组折衷解。从图2中可以看出,相比MOE,MDSRL能够寻找到更加集中于底角附近的个体,即那些具有低平均文件不可用性、低负载变化和低能耗的个体。这能够在一定程度上说明MDSRL能够比MOE取得更好的一组折衷解。为了更加精准地度量MDSRL和MOE生成的一组折衷解的优劣程度,本文采用上文中提出的HVA指标进行评判,它能够对MDSRL和MOE生成的一组折衷解的收敛性和多样性进行评价,HVA值越大,说明生成的一组折衷解的收敛性和多样性越好。图3是MDSRL和MOE的HVA值随文件总数变化时发生改变的折线图。

Fig.3 HVA comparison图3 HVA值比较
从图3可以看出,MDSRL的HVA值始终保持稳定而且十分接近于1,这能够说明随着文件总数的增加,MDSRL生成的一组解的均匀性和收敛性始终较好,而MOE算法的HVA值随着文件总数的增加并不稳定,并且始终比MDSRL的HVA值低,这说明MOE生成的折衷解在均匀性和收敛性上没有MDSRL好,并且随着文件总数的增加,解的均匀性和收敛性不能得到保证。
图4描述了MDSRL、MOE和MORM生成的最终解相比开始初始化生成的解在三个目标上效能的平均提升比例。由于初始化得到的是一组解,而MDSRL以及MOE最后生成的也都是一组解,因此取这些解的平均值,然后再与MORM得到的一个最优解进行比较。可以看出MDSRL在平均文件不可用性上以及能耗上优于MOE,但是在负载均衡上稍逊于MOE。MDSRL在平均文件不可用性和负载均衡上优于MORM,但是在能耗上稍逊于MORM。另外,从图4中可以看到MORM在平均文件可用性上的提升比例为负数,这是因为MORM对目标函数进行线性加权时没有对目标函数进行归一化并且采用的权重比例相同,这会导致数量级高的目标函数实际的权重更大。由于能耗的数量级是最大的,导致MORM在能耗上的表现比MDSRL和MOE更好,但是在文件可用性和负载均衡上表现比MDSRL和MOE都差,甚至在文件可用性上的效能提升比例为负数,这是因为文件可用性的数量级最小。减少能耗是以增大平均文件不可用性为代价,导致不能生成一个折衷解。
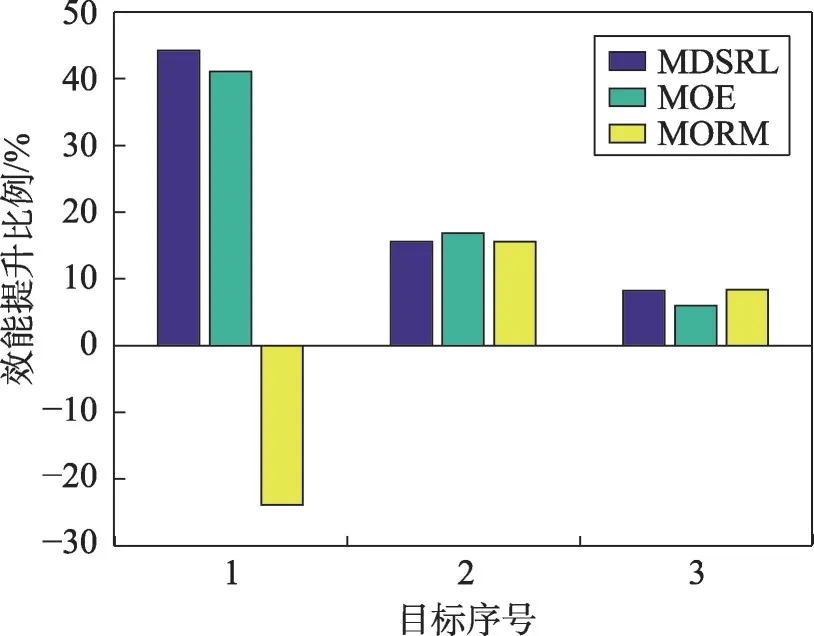
Fig.4 Efficiency of performance improvement图4 效能提升比例
图5将提出的三种算法在副本因子上进行了比较,发现相比现有的分布式文件系统都将副本因子设置为3,MDSRL、MOE和MORM都是根据文件自身的特征进行动态变化。从前面的实验结果分析可知,相比直接固定副本的个数,动态调整文件的副本数目能够有效提高系统的效能。

Fig.5 Comparison of replication factor图5 副本因子比较
图6(a)到图6(c)分别描述了三种算法在平均文件不可用性、负载变化和能耗三个目标的效能比较情况。
图6(a)描述了MDSRL能够比MOE和MORM取得更小的平均文件不可用性,相比MOE和MORM,它分别减少了3.11个百分点和68.1个百分点的平均文件不可用性。
图6(b)描述了MDSRL在负载变化目标方面稍逊于MOE,稍优于MORM,它比MOE增加了1.3个百分点,比MORM减少了0.2个百分点。
图6(c)描述了MDSRL在能耗方面优于MOE,稍逊于MORM,它比MOE减少了2.3个百分点的能量消耗,比MORM多了0.8个百分点的能量消耗,当文件个数越来越多的时候,MDSRL的能耗反而会比MORM少,可见随着文件个数的增加,MDSRL的节能效果更明显。从图6(c)可以看出,当文件个数达到300个时,MDSRL比MORM减少了0.9个百分点的能量消耗。
从图6(a)到图6(c),可以观察到MDSRL比MOE在平均文件不可用性以及能耗上能够取得更好的效能,在平均文件不可用性以及负载均衡上比MORM更优,在文件个数较少的时候比MORM在能耗上效能略差,但是当文件总数增多之后能够在能耗上取得比MORM更好的效能。

Fig.6 Efficiency comparison图6 效能比较
综上所述,MDSRL在三个目标上至少有两个目标比MOE和MORM更优,在另一个目标上稍逊或者基本相当,因此MDSRL在三个目标上都能取得不错的表现,且所求的一组折衷解在分布性和收敛性上更好。
6 结束语
本文主要考虑包括副本因子和副本放置策略在内的副本布局问题,为了解决副本带来的效能提升和能耗之间的冲突,提出了一种基于多目标分解策略的副本布局算法MDSRL,对平均文件不可用性、负载均衡、能耗三个目标进行优化,利用分解策略将多目标优化问题分解成多个标量子问题同时进行优化,试图寻找一组在这三个目标上都能取得良好效果的折衷解。实验结果表明,MDSRL至少在两个目标上都能取得比MOE和MORM更好的表现,且生成的折衷解的分布性和收敛性更好。当多目标个数多于三个时,种群中非支配解的个数急剧增加,很难得到一组在各个目标上都表现良好的折衷解,因此在未来的工作中将进一步研究超高维多目标的副本布局优化模型,以探寻更合适的副本布局多目标优化算法。

