面向时序图的K-truss社区搜索算法研究*

徐兰天，李荣华，王国仁，王 彪

北京理工大学计算机学院，北京 100081

1 引言

当前世界信息技术日新月异，每天都会产生大量的信息，越来越多的信息可以组成图结构的数据。在现实世界的许多网络，如社交网络[1-2]、化学网络[3]和图像处理[4-5]等都可以应用图网络。

近年来，图论研究提出用团来解决大图数据中的社区发现问题，即用团来描述大图数据中联系紧密的社区结构。然而团的定义过于严格，在很多情况下不能得到理想的结果，而且极大团的查找都是

NPC（non-deterministic polynomial complete problem）问题。幸而近期又出现许多类团结构，例如K-truss、Kcore等。K-truss结构能很好地体现出紧密社区结构中各节点的关系，其定义的要求要弱于定义严格的团结构，但是大于K-core。最重要的是，K-truss的查找不再是NPC问题，可以大大提高算法效率。

在现实生活中，实体间的联系并不是一成不变的，他们会随着时间而变化，或者实体间的联系本身就带有时间属性。比如在电话的通信网络中，一通电话的双方可以作为两个节点，打电话的行为会在两点间建立边的联系；在学者协作网络中，一个协作出版物的合作学者可以作为节点，协作出版物的出版会使各学者直接形成边联系。然而以上两种边的联系不是永久持续的，电话的通信联系会在电话挂断后被终止，协作出版物出版后学者的联系也会终止。在这种情况下，如果忽略边的时间属性会丢失大量信息。

本文的主要贡献在于基于K-truss模型提出了一种新的适合于时序图数据的持续社区模型，还提出了一种近似线性时间的时序图社区搜索算法。

2 相关工作

当前K-truss的研究主要体现在以下几个方面：第一是关于大图数据无法整个读入内存时的搜索算法，如Wang等改进了现有的K-truss内存算法并提出两种有效的I/O算法来处理无法在主存储器中完成的大规模网络[6]；王岩改进了基于内存的极大K-truss求解问题，并提出了基于上下界值的极大K-truss求解算法[7]。第二是将已有的串行算法改写为分布式并行算法，如王邠等提出了基于GAS（gather-applyscatter）模型的K-truss分解算法，解决了传统并行算法重复性计算和不能有效处理相互依赖的数据等问题[8]；Alemi等提出了在Spark平台下K-truss结构的分布并行算法[9]。第三就是K-truss结构在一些特殊的图数据上的应用，如齐宝雷提出了从不确定图数据中挖掘K-truss紧密子图模式的问题[10]；魏天柱提出了基于K-truss社区模型的紧密社区查询问题[11]。第四是关于K-truss结构节点特征的研究，如杨李的基于扩散K-truss分解算法识别最有影响力节点的研究[12]；王成成对非属性图和属性图中的社区搜索问题进行了研究[13]。

在时序图方面，韩文弢提出了关于时序图的存储和并行分析算法[14]；Paranjape等将时序图定义为时序边上的诱导子图，并设计了计算时序图的快速算法[15]。

关于时序图的社区发现，Wu等设计了大规模时序图下K-core模型的并行算法[16]；关于时序图下持续社区结构的研究，Li等设计了时序图下持久社区搜索算法，主要应用了K-core模型[17]。然而，K-core模型搜索的持续社区还比较大。为了获得更紧密的持续社区，本文研究基于K-truss模型的时序社区搜索，并将在后面与K-core模型对比。

3 基础知识

定义一个无向无权的简单图G，用VG代表属于G的所有节点的集合，用EG代表属于G的所有边的集合。令m=|VG|为简单图G中的节点总数，令n=|EG|为简单图G中的边总数。令nb(v)为所有与节点v有直接边相连的节点的集合，即nb(v)={u:(u,v)∈EG}，令deg(v)为所有与节点v直接相连的节点的个数，即deg(v)=|nb(v)|，deg(v)也被称为节点v的度。

定义图G中的三角形结构，三角形结构是一个长度为3的环，对于节点u,v,w∈VG，三个节点形成的三条边e=(u,v),e1=(u,w),e2=(v,w)，都有e,e1,e2∈EG。该三角形记为△uvw，定义图G中的所有三角形组成集合△G，则有△uvw∈△G。

定义1（边的支持度）对于图G中一条边e=(u,v),令sup(e,G) 代表边e在图G中的支持度。sup(e,G)=|△uvw:△uvw∈△G|，即边e在图G中所有参与形成的三角形个数。为了书写简单，本文用sup(e)代替sup(e,G)。

定义2（K-truss定义）K-truss是图G的一个极大的子图，记为Tk(k≥2)。K-truss要求子图Tk中的任何一条边在Tk中的支持度大于等于k-2，即∀e∈ETk,sup(e,Tk)≥(k-2)。根据定义，易知2-truss就是图G本身。

时序图与简单图的主要区别在于为边添加时间属性。在时序图中，边定义为e=(u,v,T)，T={t1,t2,t3…}。tn为边每次出现的时间点或时间片段，T为边所有出现的时间片段的集合。对于某一具体时刻的边也可用(u,v,t)表示。

4 时序图的K-truss社区搜索算法

4.1 时序图K-truss结构定义

由于本文使用的数据集的每条时序边上都标记一个时间戳，本文参考Li等对K-core持续社区结构的定义[17]，给出K-truss持续社区结构的定义。

定义3（持续时间段）定义一个时间间隔Δ，存在一个时间区间[ts,te]，te-ts≥Δ。这个时间区间成为边（三角形）的持续时间段需要满足以下两个条件：

（1）∀t∈[ts,te-Δ]，边（三角形的三边）的时间戳都能投影到[t,t+Δ]区间内。

（2）[ts,te]不存在一个子区间也满足（1）条件。

如图1所示，边(u,v)对于坐标轴上的4表示边(u,v)在4时间出现，记为边(u,v,4)。令Δ=3，根据定义3，边(u,w,1)的持续时间段为[-2,4]，边(u,w,1)及其持续时间段在图1中以蓝线标识；边(v,w,2)的持续时间段为[-1,5]，边(v,w,2)及其持续时间段在图1中以红线标识；边(u,v,4)的持续时间段为[1,7]，边(u,v,4)及其持续时间段在图1中以绿线标识。由边(u,w,1)、(v,w,2)、(u,v,4)三边组成的三角形的持续时间段由三边持续时间段的最晚开始点（即边(u,v,4)的开始时间1）到最早结束点（即边(u,w,1)的结束时间4），即[1,4]。同理，由边(u,w,1)、(v,w,5)、(u,v,4)三边组成的三角形的持续时间段为[2,4]，但该时间段长为2，不满足te-ts≥Δ的条件。由边(u,w,8)、(v,w,5)、(u,v,4)三边组成的三角形的持续时间段为[5,7]，不满足te-ts≥Δ的条件。

Fig.1 Temporal networks图1 时序图

由于边参与形成的三角形都有其对应的持续时间段，那么边在不同时间段的支持度也不同。边在一个时间段同时参与构成的不同的三角形个数为边在该时间段的支持度。

以图1为例，令k=3。边(u,v)只对应一条时序边，即边(u,v,4)，其在[1,4]三个时间段参与组成了△uvw，去掉重复时间段后，则其在[1,4]时间段的支持度为1。同样的，图1中边(v,w)对应两条时序边，即边(v,w,2)和(v,w,5)。边(v,w,2)在[1,4]时间段参与形成了△uvw，边(v,w,5)在所有时间段都没有参与形成满足条件的△uvw，去掉重复时间段后，则边(v,w)在[1,4]时间段的支持度为1。

定义4（边的持续时长）一条边的所有支持度不小于k-2且不重叠的时间段的总时长，称为该边的持续时长。边e在支持度为k-2下的持续时长的计算有以下公式：

式中，G为边所在的极大的子图结构；r为满足条件的时间段总数；tei为第i个时间段的结束时间；tsi为第i个时间段的开始时间。

根据定义4，边(u,v)的持续时长为3，边(v,w)的持续时长也为3。

定义5（时序图K-truss定义）对于极大的子图G中所有边e，给定一个时间长度θ：

∀e∈EG,F(e,Δ,k,G)≥θ

则G为(k,Δ,θ)-truss结构。

例如图1中的(u,v)、(u,w)、(v,w) 三边可组成(3,3,3)-truss结构。

4.2 时序图中三角形持续时间的计算

时序图中支持度要先求出图中所有存在的三角形及其持续时间段。遍历每条边，找到边的两节点的所有公共邻居节点。取邻居节点，与待求边的两点一起可以确定三条边，循环遍历三条边的所有时间戳，寻找是否在某一时间段形成了三角形。

假设有三边分别在a、b、c三个时间戳出现，为了保证形成的三角形满足te-ts≥Δ，须保证：

一种判断是否形成三角形的方法可用三条边的时间戳两两做差，若三个差的绝对值都不大于Δ，则三角形可以形成，其存在时间段为三边最晚的开始时间到三边最早的结束时间。

三个点形成的三角形可能在多个时间段出现，而这些时间段可能会有重叠，本文用如下方法将存在重叠的时间段合并。

（1）将所有ts、te放到一起按从小到大排序。

（2）设置标识符flag=0，将时间点从小到大遍历。如当前读入为，则flag加1，如果此时flag=1，则用begin保存当前时间点。如果当前读入为，则flag减1，如果此时flag=0，则用end保存当前时间点。并将(begin,end)组成时间区间保存下来。

（3）重复（2）操作，直到所有点读完，此时保存下来的就是该三角形的没有重叠的持续时间段集合。

假设一个三角形已求出其存在时间段为[1,5]、[2,6]和[7,11]。用+1和-1标志区分时间段的开始时间和结束时间，根据（1）排序可得：

根据（2）读入(1,+1)和(7,+1)时flag=1，为begin；读入(6,-1)和(11,-1)时flag=0，为end。最终保存(1,6)、(7,11)两个时间段，实现了去重操作。

三角形持续时间的计算首先要遍历图中所有边，边集大小为m。取每条边的两点的邻居集合求交，可使用有序集合求交的方法，令点的邻居集合的平均大小为nb(u)，则复杂度为O(nb(u))。遍历邻居集合的交集中的点，三点确定三条边，遍历三条边的时间戳集合，判断是否可以形成三角形。令边的平均时间戳个数为s，则此处复杂度为O(s3)。时序图下三角形的持续时间段的计算的时间复杂度为O(m×nb(u)×s3)。

4.3 时序图中边的支持度的持续时间段

支持度的持续时间要根据4.2节中的边参与形成的三角形及其持续时间段。

（1）一条边参与形成若干三角形，每个三角形有若干持续时间段，对每个时间段的开始时间设置标签值为+1，对结束时间设置标签值-1，将所有这些时间段的起止时间放在一起排序。

（2）按从小到大的顺序读取排序结果，设置一个degree初始化为0。每读一个时间点，就在degree加上标签值，degree值每变化一次就保存当前的时间段的起止时间及当前degree值，直到所有排序结果被读完。

算法1时序图下边的支持度及持续时间

假设一条边参与形成了两个三角形，一个持续时间段为(1,5)和(4,7)，另一个持续时间段为(4,7)，则：

根据算法1可得，这条边的支持度的持续时间为(1,4,1)，(4,5,2)，(5,6,1)，(6,7,2)，(7,9,1)。

算法1主要计算时序图下边的支持度和其持续时间段。要先遍历所有边，为m。对于每条边，要遍历它所有参与形成的三角形。令边参与形成的三角形的平均个数为x，则时间复杂度为O(m×x)，空间复杂度为O(m)。

4.4 时序图K-truss结构的产生与输出

利用4.3节计算出一条边的支持度的持续时间段，可根据定义4算出其持续时长，若持续时长不足θ，则将该边加入待删除边的队列，并将其标志位置0，用来标记该边已经进入待删除队列，在后面进行支持度更新操作时，就无需更新该边。在所有持续时长不足θ的边都入队后，顺次取队首边。因为队首边即将被删除，所以队首边参与形成的所有三角形都被破坏。遍历该边参与形成的所有三角形，更新被破坏的三角形的剩余两条边中还没有进入删除边队列（标志位不为0）的边的支持度。如果在被更新边的支持度减小之后，其对应时间段内的支持度不再大于等于k-2，此时就要减少其支持度的持续时长。检测更新后边的持续时间长度，若变得不足θ了，就把这条边加到待删除边队尾，并将其标志位置0。这样重复操作，直到待删除边的队列为空，此时所有剩余的边就组成了(k,Δ,θ)-truss结构。

算法2时序图下(k,Δ,θ)-truss

令ETe为e参与形成的三角形持续时间段

如图2所示，设边uy在时间6出现，除边uy以外的其他边在时间3出现。如果要在图2中查找(5,3,15)-truss结构，根据4.2节和4.3节可得边uy支持度为3，持续时长为9；边uv、vy、uw、wy、ux、xy支持度为3，持续时长为15；边vw、vx、wx支持度为3，持续时长为18。其中边uy的持续时间不足15，进入删除队列。边uy参与形成了△uvy、△uwy和△uxy。3个三角形被破坏后，边uv、vy、uw、wy、ux、xy的持续时长边为12，也要加入删除队列。进一步删除并更新边的持续时长，边vw、vx、wx也不再满足条件。因此最终结果是图2中不含(5,3,15)-truss结构。

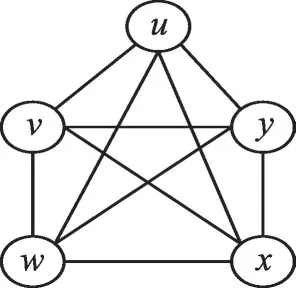
Fig.2 Example graph图2 示例图

算法2主要是时序图下边的(k,Δ,θ)-truss结构的输出，要先处理所有删除队列的边，为O(m)。对于每条边，要遍历它所有参与形成的三角形并更新所有被影响边的支持度及持续时间。令边参与形成的三角形的平均个数为x，时间复杂度为O(x×m)，空间复杂度为O(m)。

5 实验分析

5.1 运行测试

本文实验测试所使用的软硬件环境为:

（1）操作系统是Windows 10家庭中文版;

（2）硬件环境是Intel®CoreTMi5-8400 CPU @2.80 GHz，8 GB RAM。

本文使用了4个不同情境的真实世界的数据集。表1介绍了4个数据集的基本情况。Irvine messages是加州大学欧文分校的在线学生社区用户之间的已发送消息构成的时序图，边(u,v,t)代表用户u给用户v在时间t发送了消息；DNC emails是2016年美国民主党委员会的电子邮件网络，边(u,v,t)代表成员u给成员v在时间t发送了邮件；Digg是社交新闻网站Digg的用户相互回复的时序网络，边(u,v,t)代表用户u给用户v在时间t进行了回复；Haggle是一个用无线设备测量的人与人之间接触的网络，边(u,v,t)代表人物u与人物v在时间t距离在一定范围以内，视为存在一次人类接触。所有数据集可在http://konect.uni-koblenz.de下载。

Table 1 Introduction of datasets表1 数据集介绍

4个数据集的运行测试结果如表2所示，表示该数据集在Δ和θ参数下，能搜索到的K-truss结构的最大K值。

Table 2 Test results for different datasets表2 不同数据集的测试结果

K-truss搜索算法与TGR（temporal graph reduction）算法[17]（K-core搜索算法）对比测试结果如表3所示。在相同数据集和相同的参数情况下，K-truss结构的搜索结果要明显小于K-core结构。由于K-truss结构要考虑三角形的持续时间，要比K-core结构的运行时间和内存占用大一些。

Table 3 Comparison of test results表3 对比测试结果

5.2 参数分析

本节使用的数据集是Irvine messages，表4和表5主要调节Δ和θ两个变量，观察最大K-truss结构的k值和程序的运行时间和内存占用情况。

通过表4，可以发现尽管所有搜索到的极大Ktruss结构都不太大，但随着Δ和θ的增大，还是可以搜索出稍大的K-truss结构。

Table 4 Operating results of different parameters 1表4 不同参数的运行结果1

Table 5 Operating results of different parameters 2表5 不同参数的运行结果2

此外还可以发现，算法的时空复杂度与Δ和θ有很大关系，随着Δ和θ的增大，算法运行时间越来越长，内存占用越来越大。这是因为算法2的时间复杂度为O(x×m)，随着Δ的增大，就有更大的机会形成更多的三角形，x增大，时空消耗上升明显。

表4中Δ=θ，在表5中则是2×Δ=θ。通过对比不难看出，增大了对持续时间的约束，极大K-truss结构的k值就会下降，但运行时间和内存占用变化并不十分明显，这是因为无论Δ和θ如何变化，在程序初始时计算边参与形成的三角形及其持续时间，与边的支持度及其持续区间的过程中，与θ的值关系不大，主要到了最后时序图K-truss结构输出的过程中，θ的值更大会使更多的边在初始状态下即不满足持续时间的要求，会稍稍提高算法的效率。

然而，θ的值变大会导致极大K-truss结构的k值变小，当θ的值达到一定的临界值，会导致极大Ktruss结构即为初始图本身，即2-truss结构，此时算法就会失去意义。

Δ和θ值的选择也要基于数据集的情况。对于时间戳密集的数据，就要选取比较小的Δ和θ值；对于时间戳稀疏的数据，就要适当放大Δ和θ值。选定Δ和θ值后，可逐渐增大k的取值，当k=k0时搜索结果不为空，且k=k0+1时的搜索结果为空，则k0为最大k值。因此选择恰当的Δ和θ值对K-truss结构的社区搜索十分重要。

5.3 结果对比

下面将K-truss结果与K-core和K-团进行对比，如图3所示，对于同一个原始图，分别用K-core、Ktruss和K-团来计算。

Fig.3 Compared graph图3 比较图

如图3所示，对于原图（a），图（b）所示3-core结构并没有删除很多的点和边，与原图区别不大；而图（d）所示K-团中只有由4个点构成的4-团，一个5-团都没有，这样的社区太小，还比较分散，也不能完整地展示一个足够规模的社区，而图（c）所示4-truss结构比较好地保留了原图中的核心节点，根据定义4-truss结构建立在3-core的基础上，去掉了3-core中那些联系不够密切的点。4个图的规模比较如图4。

K-truss结构介于K-core结构与K-团结构之间，比较适合对联系紧密的社区的搜索。

Fig.4 Subgraph size comparison图4 子图规模比较

6 结论及未来工作

本文以非时序图下K-truss结构的搜索算法和时序图的定义为基础，通过对时序图数据的特点和Ktruss结构的性质分析，给出了时序图下K-truss结构的定义，设计了基于时序图的K-truss结构的社区搜索算法，并对算法进行了对比测试。

下一步的工作将深入分析时序图K-truss结构搜索过程中的规律,提高算法效率。