移动目标信号博弈的防御最优策略选取*

孙 岩，姬伟峰，翁 江

1.空军工程大学研究生院，西安 710177

2.空军工程大学信息与导航学院，西安 710177

1 引言

日益严重的信息安全事件对网络空间造成巨大威胁[1]，防火墙、入侵检测、身份认证、防毒软件和漏洞修补等安全反应措施属于堡垒式的刚性防御体系。这种基于先验知识的静态被动防御体系难以应对未知攻击，导致了防御者在网络空间对抗中长期处于劣势地位，形成了“小攻大防，一点攻全局防”的不对称局面[2]。美国科学技术委员会提出了移动目标防御技术(moving target defense，MTD)，该技术是改变攻击和防御不对称状态的新方法，目的在于提高信息系统多样性、动态性和随机性的特征，增大攻击成本，提高抗攻击能力。

但滥用MTD技术并不一定会提高防御能力，反而可能会增大防御成本、降低系统利用效率。如在网络交换服务中，随意更改连接方式会导致用户无法访问服务器。因此如何实施合理MTD策略，在攻击者不断更新攻击策略时，最大化防御收益是目前研究的热点。

博弈论已经被证明可以在经济学、生物学和其他领域做出非常有效的重要决策，它是研究各博弈方竞争对抗的策略选择理论[3-4]。网络空间对抗所展现出来的目标独立性、策略依存性和非合作性与非合作博弈的特征基本一致。本文以信号博弈模型为基础框架，描述网络攻防之间的博弈关系。

在基于博弈论的网络防御策略选取研究中，构建模型需要关注四个关键问题：博弈双方是否可以异步（动态）行动；博弈信息是否完全；博弈阶段是否单一；博弈双方收益量化方式是否具有代表性。

文献[5]采用完全信息静态博弈模型进行研究，定义了攻击面概念，量化转移攻击面的收益与成本，对系统安全性与可用性之间的均衡策略选取进行研究。但其规定攻防双方必须同步行动，即静态博弈性与实际网络空间攻防状况不符。文献[6]与文献[7]引入完全信息动态博弈理论。文献[6]构建随机博弈模型展开网络攻击研究。文献[7]利用攻击图构建二人零和Markov博弈模型，通过监控云网络中的攻击流量，识别攻击者最优攻击策略，设置相应对策以强迫攻击者选择次优策略。但现实网络攻防双方的关系对立，攻击者与防御者都会阻止对方进一步获取自身信息，因此文献[5-7]中完全信息博弈模型的现实应用价值不高。

为避免上述静态性和完全信息性的限制，部分文献以不完全信息动态博弈为研究基础。文献[8]提出MP2R防御模型，直观描述防御者与合法用户或攻击者之间的交互过程，分析其均衡条件，设计一种网络安全防御机制，但仅体现在理论层面，未能与真实网络环境相结合，应用性较弱。

在现实网络对抗环境中，大部分网络攻防都属于一种“‘明’防‘暗’攻”的情况。防御者一般难以获取相关攻击者信息。一般情况下，防御者对信息服务、商业利益等需要的客观因素使得攻击者可以通过公共平台收集防御者相关信息，例如防御等级、防御技术、防御设备。攻击者通过分析防御者相关信息，进而决定是否攻击，采用何种方式攻击。这种情况也使得被动防御难以招架各种攻击手段。为解决上述问题，文献[9]以防御者为发信者，提出防御伪装思想，利用防御者的公开信息干扰攻击者的正常判断。但局限于单阶段网络对抗分析，即攻防双方的策略选择行为只进行一个回合。

由于实际网络的攻防对抗往往持续多个过程，且前一阶段往往影响后一阶段的攻防行为策略选取。文献[10]从攻击面转移角度出发，以MTD策略动态性和多样性特征为基础对单阶段与多阶段攻防收益进行分析，但在攻防博弈行动顺序选择上，没有避免“‘明’防‘暗’攻”的劣势局面。文献[11]在文献[9]的基础上将单阶段博弈扩展为多阶段博弈，但文献[9,11]中的最优策略选取方法从严格意义上来说是最优伪装信号策略选取，对于可以抵御攻击的真实防御策略而言，采用等概率选择防御策略机制，这难以最大化防御效用。

除以上分析之外，最优防御策略的选取基础还取决于攻防策略收益量化。合理、全面的量化可以进一步提高防御效用。文献[12-13]在分析总结不同攻防策略分类的基础上，提出了成本、收益量化方法，文献[9,11]在此基础上对伪装信号进一步进行量化。上述量化方法均建立在防御系统属于完美系统，防御系统本身不会出现任何漏洞、缺陷和故障等。但现实情况中，以入侵检测系统为例，防御系统本身无法避免错检、漏检的情况发生。因此完美防御系统下的收益量化方式与现实场景仍然具有一定差距。

通过以上分析可知，现有的基于博弈论的最优MTD策略选取研究存在以下问题：

（1）攻防双方的完全信息性和行动同步性的假设与实际网络对抗特征不符；

（2）博弈模型中，防御者的主动性不明显，难以改善“‘明’防‘暗’攻”的防御劣势地位；

（3）局限于单阶段攻防分析，无法表现网络攻防中的多阶段性特点；

（4）基于完美防御系统的攻防收益量化分析方式容错性较低。

为解决以上存在的问题，根据信号博弈基本理论[14-15]，本研究采用以防御者作为发信者，攻击者为收信者的行为模式。利用攻击者通过探测行为获取防御情况的方式，防御者发送诱导信号干扰攻击者。在此基础上，考虑防御入侵检测系统存在错检情况的不完美性，提出移动目标信号博弈防御模型（moving target signal game defense model，MTSGDM）。随着网络对抗的进行，双方愈加了解对手信念，进而不断调整自身行为，最后在精炼贝叶斯均衡求解算法的基础上，提出移动目标防御最优策略选取应为最优诱导信号策略与最优防御策略的组合策略，并给出组合策略选取算法。

2 MTSGDM博弈模型

2.1 MTSGDM博弈模型定义

定义1移动目标信号博弈的防御模型MTSGDM可以表示为九元组：

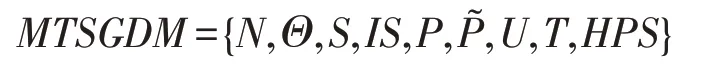
N={NA,ND}为博弈人空间，NA为攻击者，ND为防御者。还有虚拟参与人“自然”。

Θ={ΘA,ΘD}为博弈人NA、ND的类型空间，其中ΘA={θA}，表示攻击者只有一种类型；ΘD={θi|i=1,2,…,n}，n≥1，n∈N+（以下n均具有该属性）表示防御者的若干类型，且每种类型的防御能力不同。

S={A,D} 是攻防策略空间，A={ax|x=1,2,…,}n和D={dy|y=1,2,…,}n分别表示攻击策略和防御策略。一般攻击者会将攻击策略组合以进行攻击行为，Ax表示攻击者的组合策略，包括ax的一种或几种。

IS(inducing signal)表示防御诱导信号。IS={isj|j=1,2,…,n}，表示防御者释放的诱导信号策略。

P为攻击者先验信念集合，表示攻击者对防御者类型的初始判断，其中：

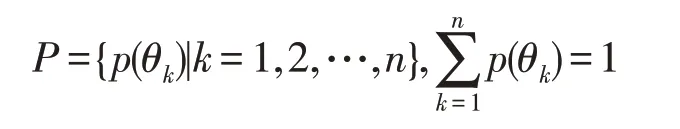
为攻击者后验信念集合，表示攻击者观察到诱导信号后，使用贝叶斯法则调整对防御者类型的判断。为简化表示，令

U=(UA,UD)是攻击者与防御者的收益函数。

Tt是多阶段博弈的阶段数，Tt={Tt|t=1,2,…,n}。

HPS(historical policy set of IS)表示防御者历史诱导信号策略集合。根据贝叶斯法则，攻击者可以通过Tt-1阶段博弈更新Tt阶段对防御者类型的推断。HPS={his(Tt)|t=1,2,…,n}，his(Tt)表示防御者在Tt阶段之前的历史诱导信号策略。

2.2 攻防收益量化

对于引言部分关于量化方式的分析，本文在前人基础上做出改进，采用以下量化方式。

定义2防御策略有效函数ε(ax,dy)。表示应对攻击ax采取策略dy的有效性，简记为εxy。成功阻止攻击时ε(ax,dy)=1，无效时ε(ax,dy)=0。

定义3攻击成本CA(attack cost)，指攻击者发动攻击a需要的成本。防御成本CD(defense cost)，指防御者采取防御动作d所需要的成本，CD一般由防御策略的操作成本CO(d)和负面成本CN(d)构成。系统损失成本SDC(ax,dy)(system damage cost)，表示防御策略dy无法阻止攻击策略ax时对系统产生的损失。系统防护收益SPB(ax,dy)（system protection benefits），表示防御策略dy能够阻止攻击策略ax时，系统所保护的资源。SDC(ax,dy)、SPB(ax,dy)通常由目标资源重要程度C(criticality)、攻击致命度AL(attacklethality)、安全属性损害SAD(security attribute damage)和防御策略有效函数εxy表示。

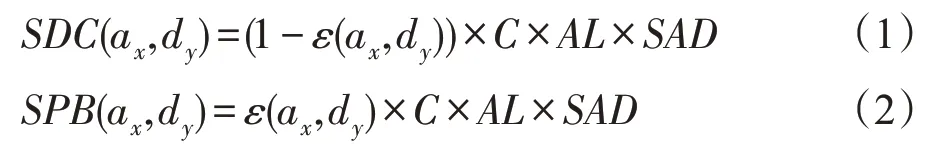
定义4相对防御收益RDG（relative defense gain）。

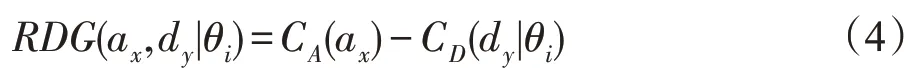
表示在防御者θi发送诱导信号isj，攻防策略分别为ax、dy时攻击成本与防御成本的差值。

定义5诱导信号成本CIS（cost of induced signal）表示防御方释放诱导信号所耗费的成本。若信号类型与真实的防御类型一致，则CIS=0。通过真实的防御者等级与诱导信号等级之间的差距对CIS进行相对量化。

定义6诱导信号分析成本CAIS（cost of analysis induced signal）。攻击者观测到诱导信号后，对诱导信号的类型进行分析所消耗的资源成本。

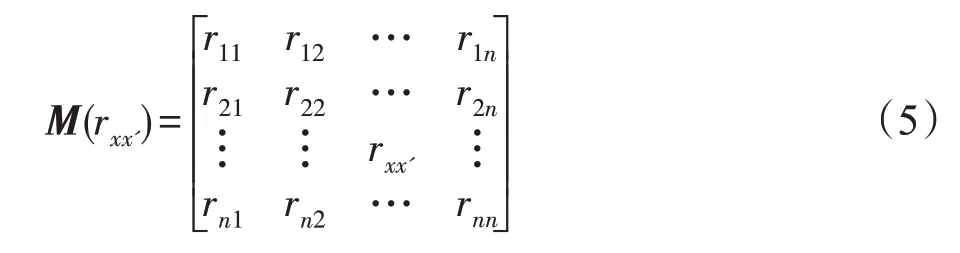
定义7错检率Red（error detection rate）。防御者的入侵检测系统无法避免存在错检、漏检情况，本文暂考虑仅存在错检情况。Red(ax→ax′)表示为将ax错检成ax'的概率，简记为rxx'，其中1 ≤x≤n,1 ≤x'≤n。当x≠x'时，表示发生错检情况；当x=x'时，表示没有发生错检情况。根据定义得到以下错检概率矩阵M(rxx')。

定义8错检损失函数λ（error checking loss cost function）表示未发生错检情况下最优防御策略收益与发生错检情况下最优防御策略收益差值。防御者选择的防御策略分为两种类型，即dy=表示不发生错检情况时，类型为θi的防御者发送诱导信号isj，攻击者发出策略ax，防御者所选取防御收益最大的防御策略，即最优防御策略。表示防御者对于攻击者发出攻击策略a-x（除ax以外的其余某种攻击策略）的最优防御策略。其中y满足条件：

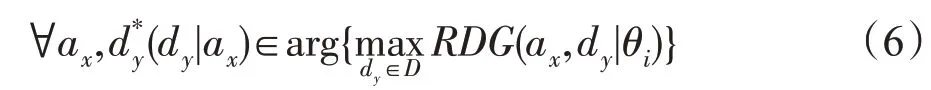
可见在该量化方式下，当攻击策略ax确定时，随之确定。但当发生错检情况时，防御者将ax误认为a-x，此时防御者选择防御策略而不是（不考虑针对一种攻击策略下存在两种防御策略收益相同的情况）。

定义9错检损失代价Cλ（cost of error detection loss）是防御者错检时带来的损失代价。即当真实攻击策略ax被误判为a-x所带来的全部错检可能情况下的损失代价。

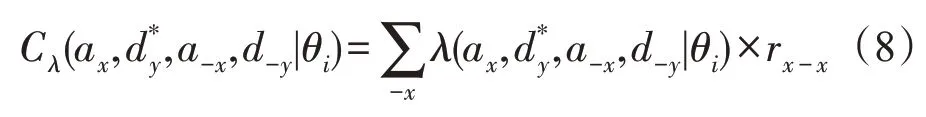
攻击收益的计算公式为：

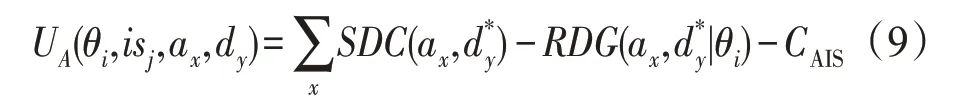
防御收益计算公式为：

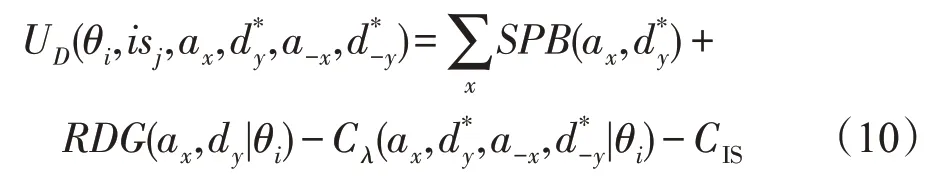
2.3 MTSGDM模型特点分析

（1）更加符合网络攻防的现实环境。充分考虑攻防信息不完全性、攻防行为异步性、攻防多回合性的特征。

（2）提升防御者主动地位。以防御者作为发信者，改变了传统网络攻防中防御者的被动局面。

（3）攻防策略收益量化更加合理、全面。以网络安全目的为出发点，引入诱导信号量化和考虑入侵检测系统可能会发生错检的情况，对攻防收益进行分析。

（4）博弈模型的通用性更好。该模型中的类型集合和策略集合均可以扩展至n。

3 均衡求解及选取最优防御组合策略

3.1 MTSGDM模型博弈顺序

MTSGDM博弈模型流程如图1所示：初始阶段，“自然”按照一定概率从防御者ND的类型空间ΘD中选择一个类型θi。防御者无法明确θi的情况下拥有对防御者类型的先验信念。

防御者依据自身类型θi，选择释放诱导信号isj以干扰攻击者对防御者类型的后验推断。

攻击者观测到信号isj后，选择攻击策略组合Ax，并更新对防御者类型的后验概率推断。防御者观测到Ax，实施最优防御策略。

攻击者将更新的后验信念作为下一阶段对防御者类型的先验推断。

一直循环以上过程，直至以下三种情况结束攻防：攻击者主动放弃攻击；攻击者成功获取防御者重要数据，对防御者造成损失；防御者成功防御全部攻击行为。

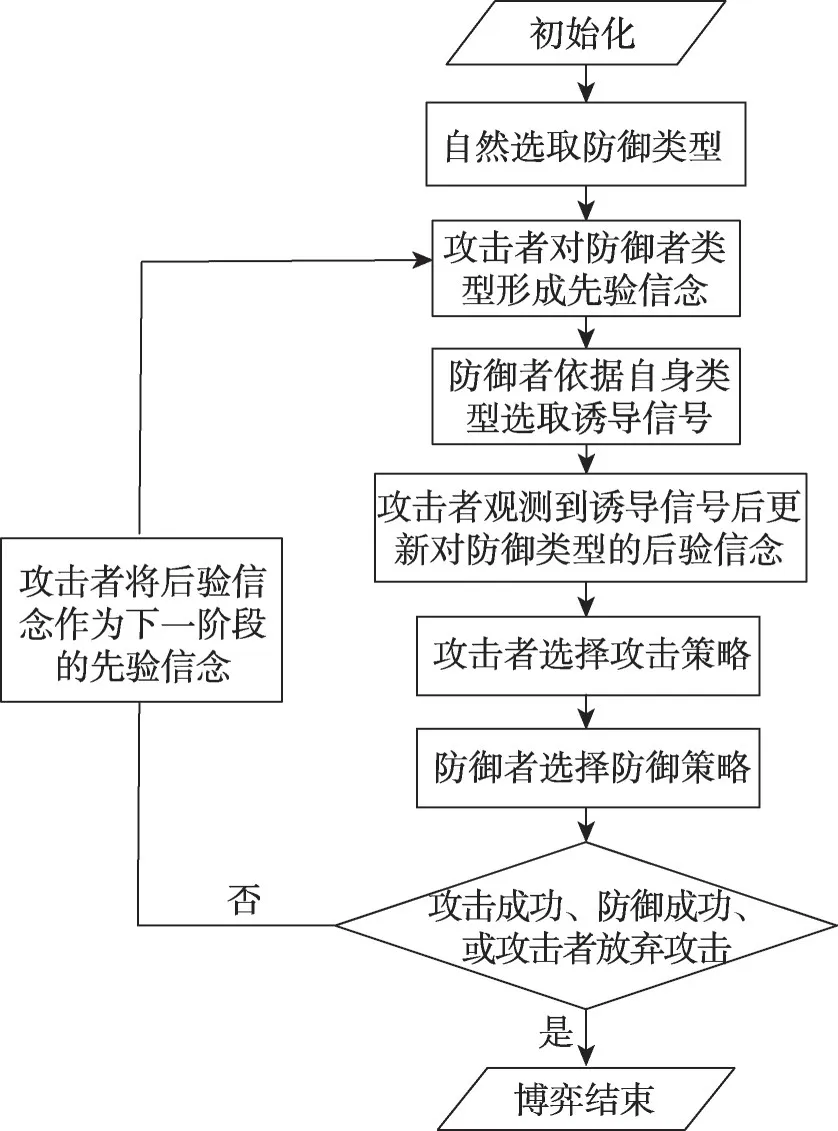
Fig.1 MTSGDM flow图1 MTSGDM流程

3.2 MTSGDM博弈模型精炼贝叶斯均衡求解

攻击者选择攻击策略前观察到防御者的诱导信号策略，应该更新对防御类型θi的信念，并且根据ΘD上的后验概率选择攻击策略Ax。在精炼贝叶斯均衡中，防御者的诱导信号策略如何选取取决于其类型，用is*(isj|θ)表示。攻击者明确is*(isj|θ)并观察到isj后，用贝叶斯法则将p(θi) 更新到，并要求对每一个isj，攻击者都要在isj的条件下最大化攻击收益。

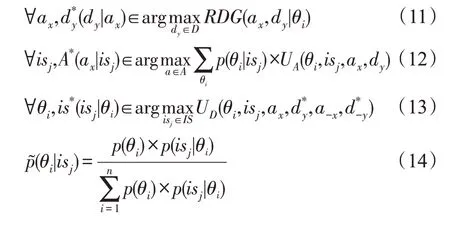
式（11）指防御者选择最优防御策略。

式（12）、式（13）为该博弈模型的完美性条件。式（12）指攻击者得出关于θi的后验信念时，做出的最优攻击策略；式（13）表示考虑isj对攻击者行动的影响后，防御者选择的最优诱导信号策略。

式（14）是运用贝叶斯法则得到后验信念的过程。

3.3 多阶段博弈贝叶斯均衡求解

为简化起见，考虑攻防双方多阶段移动目标防御中不存在收益的折扣现象，即在Tt和Tt-1阶段博弈具有相同的收益。博弈阶段次数由攻防双方决定。

根据贝叶斯法则，攻击者可以通过Tt-1阶段博弈更新Tt阶段博弈对防御者类型的判断，即攻击者会为了修正对防御者类型的判断，将Tt-1阶段攻击者对θi的后验信念作为Tt阶段的先验判断。isj(Tt)为防御者在Tt阶段的诱导信号策略。

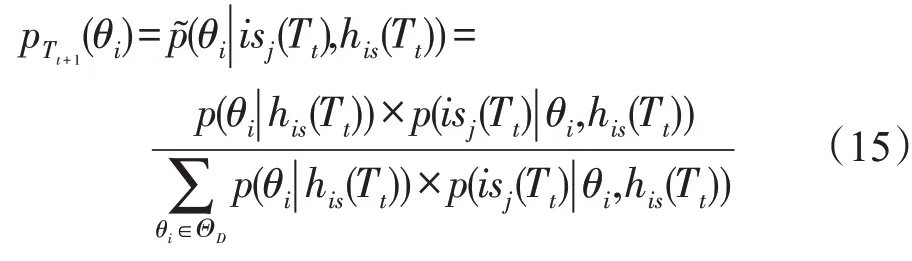
修正先验判断后，每个阶段的贝叶斯均衡求解过程与3.1节中单阶段求解过程相同。

MTSGDM均衡求解过程：

（2）攻击者建立先验概念推断p(θi)；

（3）防御者选择最优释放诱导信号策略is*(isj|θi)；

（5）利用精炼贝叶斯均衡{is*(isj,θi),a*(ax|isj)}，求出

依据前文分析，给出该模型最优策略选取算法。

Input:MTSGDM

Output:各阶段最优诱导信号策略以及最优防御策略的选择

本文给出的方法与其他文献进行比较，结果如表1所示。

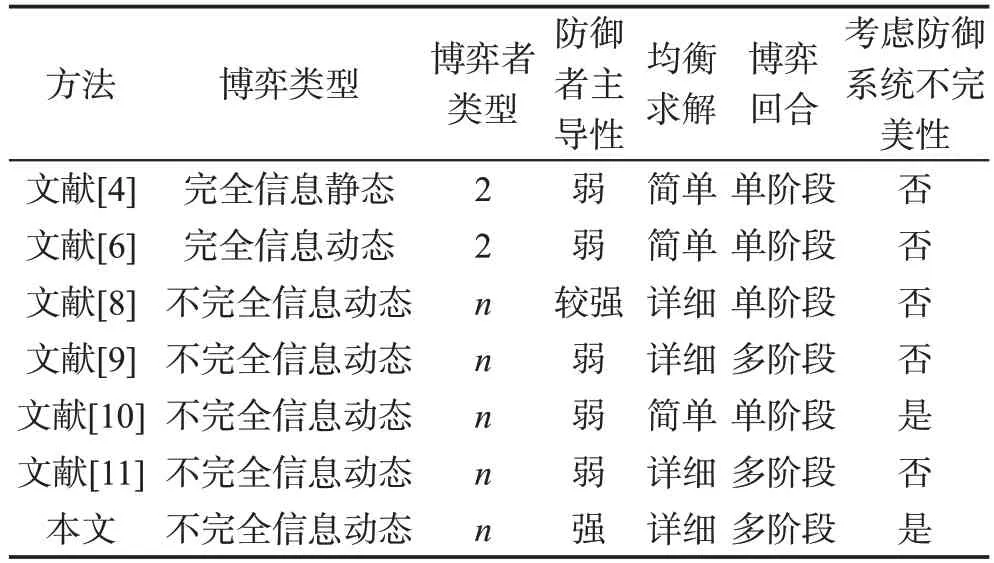
Table 1 Comparison results of different methods表1 不同方法比较结果

4 实验仿真与结果分析

4.1 实验环境描述

攻击者通过多种攻击手段破坏目标系统、窃取数据。防御者为抵御攻击，设置MTSGDM机制，当入侵检测系统检测到异常行为或异常流量后释放诱导信号，干扰攻击者选择攻击策略。为验证所提出的MTSGDM及相关均衡求解方法正确性和有效性，设计如下实验网络，拓扑结构如图2所示。

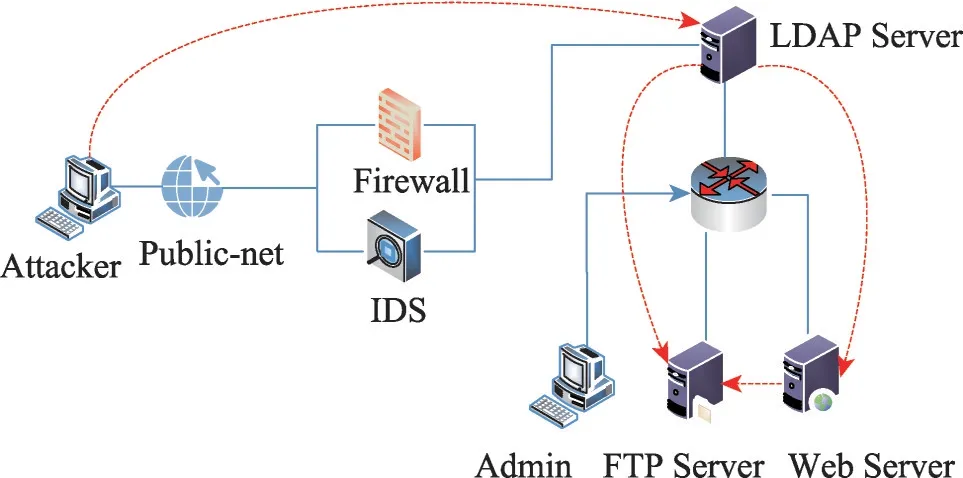
Fig.2 Experimental environment topology图2 实验环境拓扑结构

该系统主要由安全防御设备、LDAP Server、Web Server和FTP Server组成。防火墙的安全策略为仅允许网络用户访问LDAP Server，其他网络节点和端口进行阻断；LDAP Server可以访问Web Server和FTP Server。攻击者的目的在于获取FTP Server的特权，窃取数据。攻击者无法直接访问FTP Server，但是通过一系列原子攻击，攻击者可以获取Web Server和FTP Server的root访问权限[16-17]。使用Nessus工具扫描，挖掘实验环境设备漏洞信息，如表2所示。

攻击者通过前期探测，得到LDAP Server的IP地址及提供的服务所存在的漏洞，利用CVE-2016-5195漏洞获取LDAP Server的Root权限。根据图2虚线可知，攻击者窃取FTP Server数据有两种路径。第一种，利用CVE-2017-5095获取Web Server的Root权限，然后利用FTP Server漏洞CVE-2015-3306获取user权限；第二种，直接利用FTP Server漏洞CVE-2015-3306获取user权限。

4.2 MTSGDM收益计算

本文只考虑攻击者对LDAP Server的攻击。利用文献[12]的方法对漏洞数据和防御策略进行分析，得到攻击者可能采取的攻击策略组合A1(a1,a3)，A2(a2,a4)。根据文献[18-20]得到攻击者的原子攻击信息如表3所示。

Table 2 Equipment vulnerability information表2 设备漏洞信息

Table 3 Atomic attack information表3 原子攻击信息

该例中将防御者类型分为高防御等级和低防御等级，用ΘD=(θH,θL)表示。诱导信号空间IS=(isH,isL)分别表示伪装成高防御等级和低防御等级时的诱导信号isH和isL。θH型防御者可以选择防御策略(d1,d2)，θL型防御者可以选择防御策略(d3,d4)。并且

初始化阶段，防御者必须考虑所有可能的攻击情况以确定最优防御策略初始阶段博弈树如图3所示。

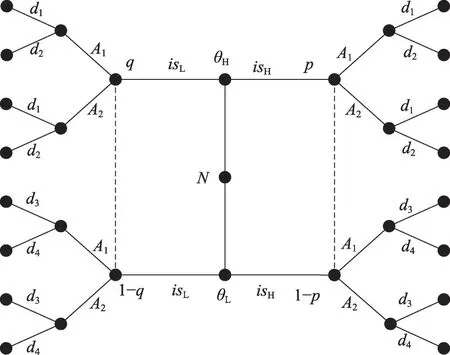
Fig.3 Game tree in initial stage of MTSGDM图3 MTSGDM博弈模型初始阶段博弈树

LDAP Server可实施的MTD防御策略如表4所示。高等级防御者采取服务架构多态化策略，该策略是指通过软件栈实现服务功能，软件栈通常包括LDAP服务器程序、LDAP应用程序、操作系统和虚拟层。通过建立多个具有唯一软件栈的虚拟服务器，建立多态化防御策略。例如“Ubuntu 14+ApacheDS”与“Windows 7+IIS 6”是在操作系统和服务器程序的两种不同实现方式。低等级防御者采取IP地址跳变和服务端口跳变策略。

LDAP Server的安全属性损害SAD=20，重要程度为C=4。通过对防御者入侵检测系统性能进行建模，可知其错检概率矩阵。由错检概率矩阵分析可知因错检而存在两种错误攻击策略A3(a1,a4)、A4(a2,a3)。

假设攻击者对防御类型的先验信念为(p(θH),p(θL))=(0.5,0.5)。计算防御收益前首先要明确全部情况下的以判断该dy是否最优。如表5所示。

根据检查概率矩阵可知，在发生错检查情况下，防御者的最优防御策略可能会发生改变，如表6所示。根据表6分析可知，发生错检时，其真实防御策略仍然有可能是最优防御策略。

4.3 精炼贝叶斯均衡求解及策略选取

在该模型下，防御者使用诱导信号以及真实防御策略的不同组合方式进行网络防御，根据表1中算法可得出第一阶段博弈量化结果，如图4所示。

防御者在该博弈模型下有4种纯策略：“自然”选择类型θH或θL,防御者均释放诱导信号isH，该策略记为(isH,isH)。同理可得(isL,isL)、(isH,isL)、(isL,isH)。在此以混同均衡(isH,isH)和分离均衡(isH,isL)为例进行求解。

Table 4 Moving target defense strategy description表4 移动目标防御策略描述

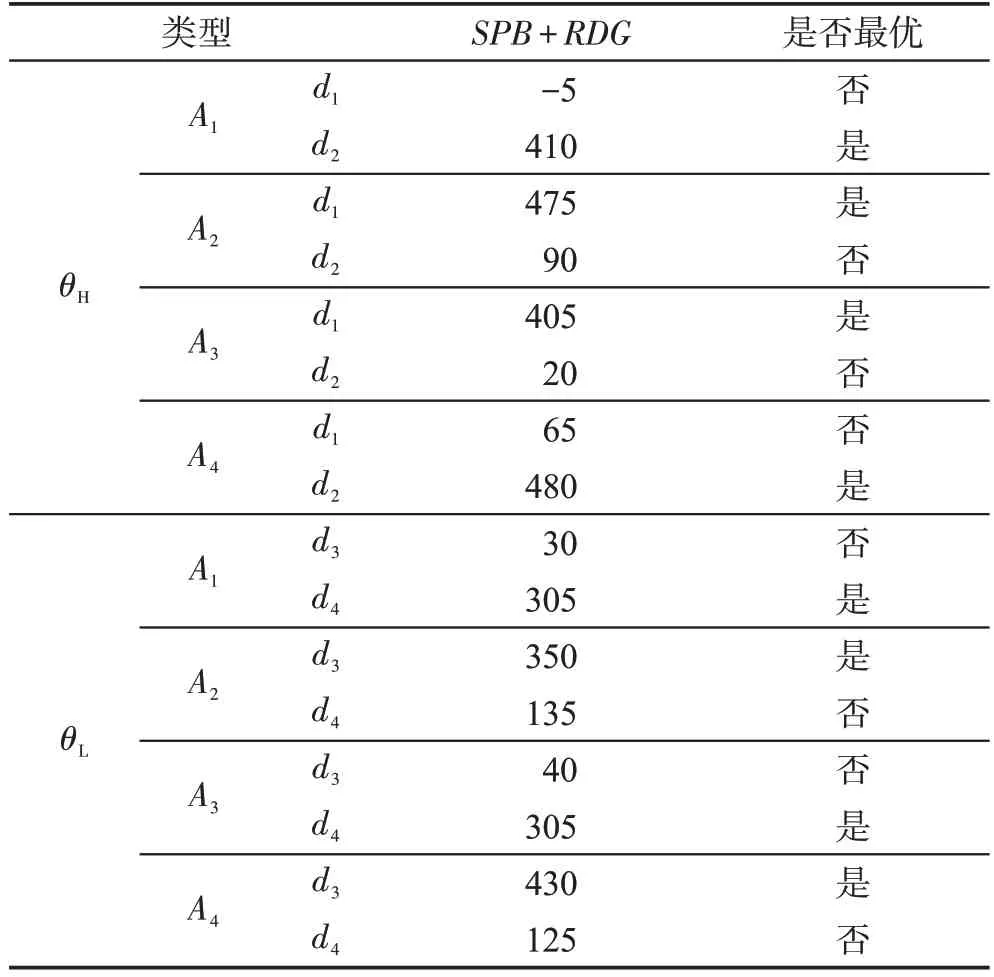
Table 5 Initial earnings quantification of SPB+RDG表5 初始阶段SPB+RDG 收益量化

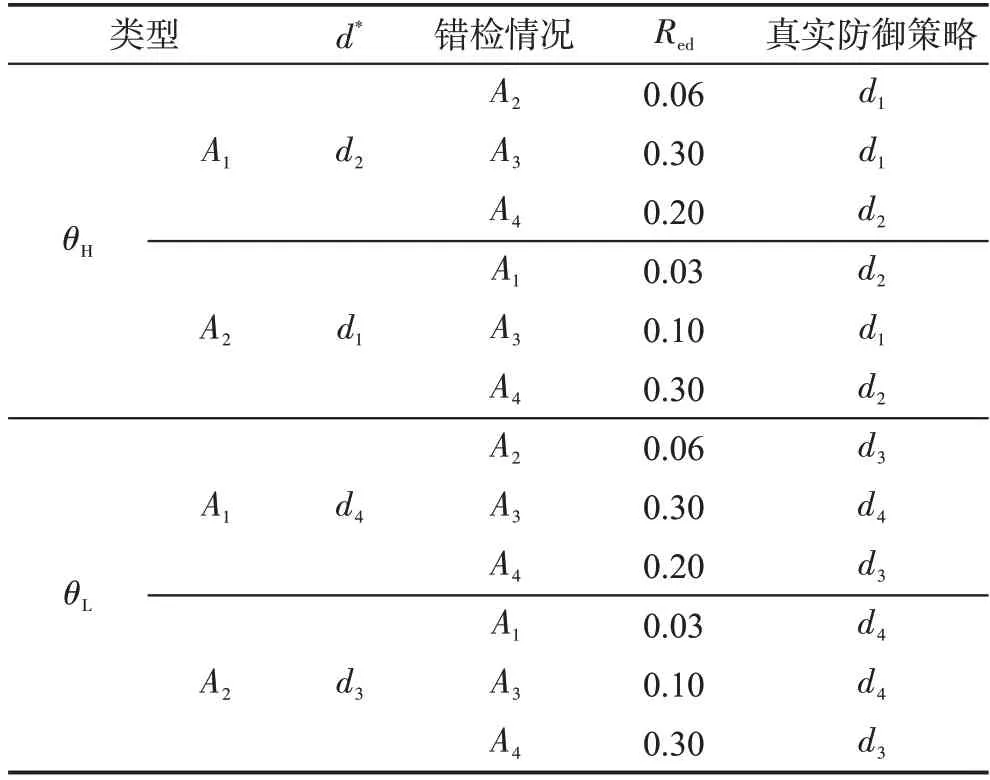
Table 6 Selection of real defense strategy under error detection表6 错检情况下真实防御策略的选取

4.3.1 混同均衡策略

攻击者对于isH和isL的信息集均衡路径之上的贝叶斯均衡推断分别为(p,1-p)、(q,1-q)。

若要使得混同均衡策略(isH,isH)为最优策略，则要保证如果防御者选择释放isL时，攻击者的选择给两种类型的防御者所带来的防御收益小于防御者选择释放isH的情况。

当且仅当攻击者对isL的反应为A1，该混同均衡策略存在。攻击者最优策略为A*(Ax|isH)=A2，A*(Ax|isL)=A1。

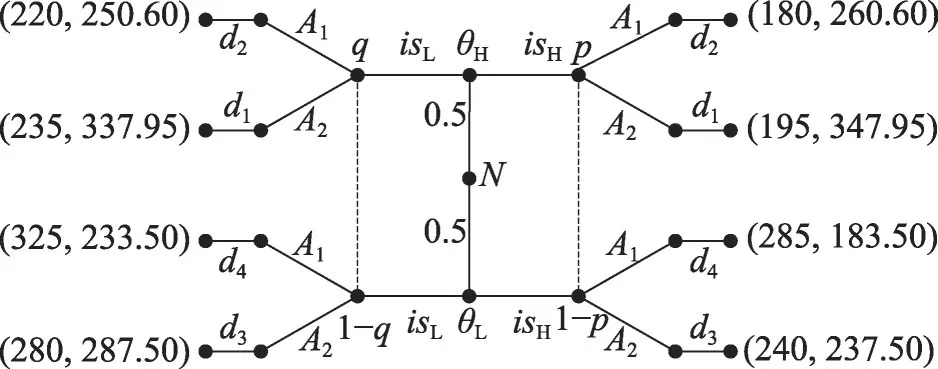
Fig.4 MTSGDM phase 1 game tree and quantitative results (UA,UD)of offensive and defensive gains图4 MTSGDM第一阶段博弈树及攻防收益(UA,UD)量化结果

利用贝叶斯公式修正(p,1-p)、(q,1-q)，可得

防御最优策略组合为：

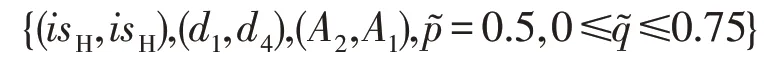
4.3.2 分离均衡策略

攻击者对于isH和isL的信息集均衡路径之上的贝叶斯均衡推断分别为(1,0)、(0,1)。

若要使得分离均衡策略(isH,isL)为最优策略，防御者选择信号(isL,isH)时，攻击者的选择给两种类型的防御者所带来的防御收益小于防御者释放(isH,isL)的收益。

仅当攻击者对isL的反应为A1，该分离均衡策略存在。攻击者最优策略为A*(Ax|isH)=A1，A*(Ax|isL)=A1。

利用贝叶斯公式修正(p,1-p)、(q,1-q)，可得

即{(isH,isL),(A1,A1),p～=1,q～=0}为博弈的混同策略均衡。

最优防御策略组合为：

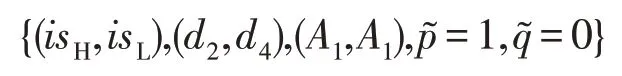
同理，求得混同策略均衡(isL,isL)、分离策略均衡(isL,isH)均不能构成该博弈的精炼贝叶斯均衡。

4.4 多阶段先验信念推演

通过对Tt时间之前的历史统计得到不同攻击类型的攻击者使用不同攻击策略的概率为p(isj|θi,his(Tt))，如表7所示。

第二阶段开始时，防御者采取策略isH，可以得到防御者类型的后验信念为：

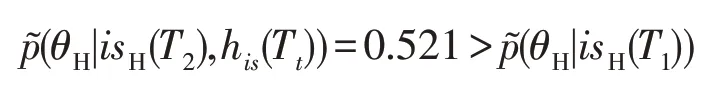
Table 7 Probability relationship p(isj|θi,his(Tt))between defense type and defense induction signal strategy表7 防御类型与防御诱导信号策略概率关系p(isj|θi,his(Tt))

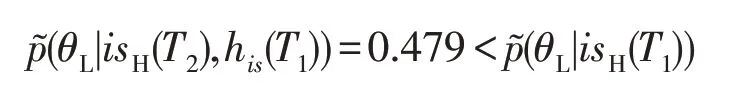
进行数学归纳后可知：

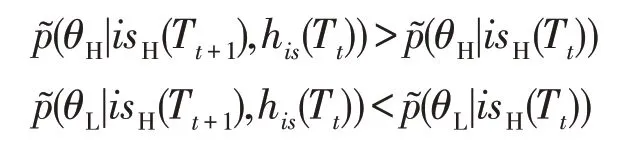
由此可知，当防御者持续采用高等级诱导信号，攻击者可以不断修正信念，增加对其高等级防御者类型的推断。

4.5 算法对比

在4.1节搭建的实验环境中，将本文的最优策略组合算法与文献[9]的等概率防御策略选取算法进行对比，结果如图5所示。其中同一颜色的点代表相同策略下不同算法的攻防收益。例如，红色代表高等级防御者θH选择高等级诱导信号策略isH，攻击者选择攻击策略A1的情况。定义公式：

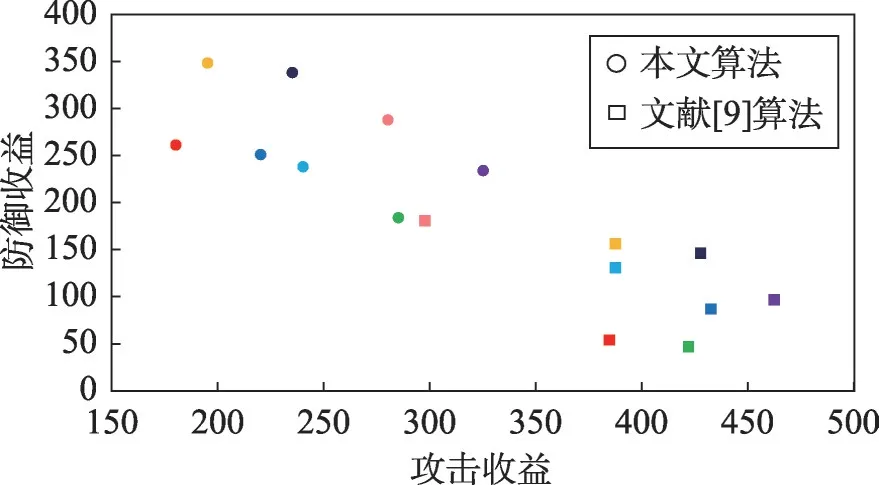
Fig.5 Algorithm comparison图5 算法对比

由图5分析可知，在考虑诱导信号以及防御系统本身不完美的情况下，本文的防御最优组合策略算法与文献[9]的等概率防御策略选取算法相比效果更好。在相同等级防御者选择相同等级诱导信号策略，攻击者选择相同攻击策略的情况下，通过式（16）、式（17）计算，得到如表8所示结果。

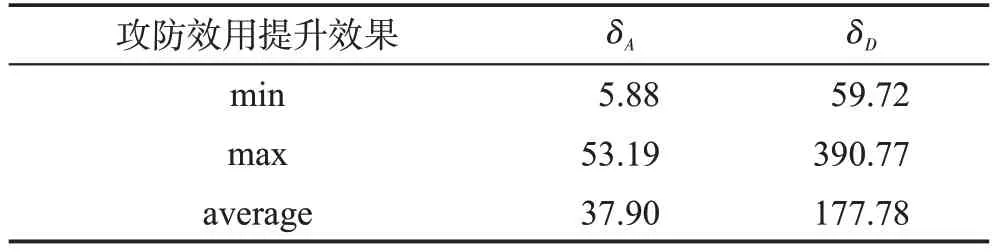
Table 8 Attack return reduction rate and defense return increase rate表8 攻击收益降低率与防御收益提高率 %

由表8可知，与文献[9]相比，平均攻击收益降低率为37.90%，平均防御收益提高率为177.78%。可以看出本文的最优诱导信号策略与最优防御策略的组合策略算法收益更高，效果更好，从攻防两端都可以为防御者带来更多的防御性能提升。

5 实验结果分析

通过对MTSGDM均衡结果和攻防收益分析，可以得到以下规律：

（1）低等级防御下MTD策略跳变周期越小，防御收益越大。

在低等级防御的情况下，无论释放任何等级的诱导信号，防御策略d3的防御收益都要大于防御策略d4的防御收益。这是因为在防御等级相差不大、对待同一种攻击策略时，跳变周期小的策略能够有效减少攻击者攻击策略的有效攻击持续时间，防御者的高频跳变手段使得同一种攻击策略无法长期有效。

（2）高等级防御下MTD防御策略的差异性越大，防御性能越好。

在高等级防御的情况下，无论释放任何等级的诱导信号，防御策略d1的防御收益都要大于防御策略d2的防御收益。这是因为在跳变周期相同的情况下，防御策略差异性越大，软件栈配置信息存在相似漏洞威胁的可能性越小。攻击者需要更长时间进行前期攻击准备，如扫描、漏洞挖掘，因而提高了防御收益。

（3）差异性大的MTD策略比跳变周期小的MTD策略防御收益更高。

无论释放任何等级的诱导信号，高等级防御下的防御策略收益普遍大于低等级防御下的防御策略。这是因为尽管高等级防御策略比低等级防御策略跳变周期长，但对改变受保护系统特征的能力而言，操作系统与服务器程序的变化比简单的端口或IP地址跳变的能力更强，即带来更好的攻击面转移效果。

（4）合适的诱导信号策略能够有效提高防御收益。

在混同均衡策略中，高、低等级防御者均应选择高防御等级诱导信号策略。这是因为高等级防御者无需隐藏自身能力，若选择低等级防御诱导信号策略反而容易导致攻击者的攻击，并且损失了不必要的诱导信号释放代价。而低等级防御者选择高等级防御诱导信号策略，是想以此威慑攻击者，达到“不战而胜”的目的。

在分离均衡中高等级防御者应选择高防御等级诱导信号策略理由与上述相同，但低等级防御者应选择低等级防御诱导信号策略，这是因为防御者考虑到伪装成本过高，即便达到威慑效果，却给自身带来了负防御收益。释放诱导信号需要付出一定的代价，若防御收益无法弥补该代价，则不应伪装自身防御等级。因此如何选择防御诱导信号策略需要结合防御者自身实际情况。

（5）防御者尽量避免长期选择同一类型的诱导信号策略。

这是因为攻击者对防御类型推断的准确性对攻防结果有重大影响，尽管攻击者不能完全掌握防御者的类型信息，但可以根据诱导信号不断使用贝叶斯法则对防御者的类型信念进行修正，并选择最优攻击策略，进而增大攻击收益，降低防御收益。

6 结束语

本文提出了移动目标信号博弈的防御模型MTSGDM，该模型充分结合现实网络中攻防动态性（异步性）、不完全信息性的特点。为防御者提供主动发送诱导信号的思想，以改变防御者在网络对抗中的被动劣势地位。同时正视防御者自身系统具有无法避免的缺陷的基础上，提出移动目标防御最优策略选取算法。在该算法中，将最优诱导信号策略与最优防御策略的组合视为防御者最优的选取策略，以此最大化防御收益。最后通过具有一定代表性的实验拓扑结构，对该策略选取算法进行实验，分析实验结果给出了MTD防御的一般性规律，对现实网络环境下的攻防策略选取具有一定的指导意义。