基于培养数学核心素养的专题复习课教学例谈
任继富

【摘要】数学核心素养是指数学学习者在学习数学或学习数学某一个领域所应达成的综合性能力,其中逻辑推理能力在数学核心素养中属于较高层级的能力。文章以专题复习为例,从解决实际问题入手,经过课堂教学渗透,培养学生逻辑推理能力,实现数学核心素养的整体提升。
【关键词】数学核心素养;推理能力;最值问题
一、由一道考题引发的思考
在中考第一轮综合复习过程中,有这样一道题目:“二次函数y=X2+4x+3图像上的点到直线y=2x的最小距离为____.”该题初看起来就是点到直线的距离问题,如果是纯几何问题,很多学生都不会觉得有什么困难,但是与二次函数联系起来后,顿时成了一道难题。
基础较好的同学容易找到解题思路。设与y=2x平行的直线解析式为y=2x+k,当y=2x+k与y=X2+4x+3图像相切时,切点到直线y=2x的距离即最小距离,联解y=X2+4x+3 y=2x+k,根据方程组只有一组解可以得出切点的坐标,然后计算切点到y=2x的距离就是最小距离。解题思路易形成,但运算量大,增加了运算的出错率。
若日常教学中我们有意识培养学生的逻辑推理能力,那么学有余力的学生会发现更简便的方法。设二次函数y=x2+4x+3图像上的一点M坐标为(m,m2+4m+3),过该点作x轴垂线,与直线y=2x交于点N(m,2m),所以线段MN=m2+4m+3-2m=m2+2m+3=(m+1)2+2,易得当m=-1时,MN有最小值2,当MN取最小值时,也就是二次函数y=x2+4x+3图像上的点到直线y=2x的距离最小,最小距离为2√5/5。
该题的解答让笔者反思日常“扁平化”的教学,教师忙于赶教学进度,学生思维训练的时间有限,教师有意或无意中把核心素养中的能力培养放到了次要位置,导致学生遇到新问题时经常陷于无从下手的窘境。
二、教学中培养学生逻辑推理能力的实践探索
在数学学习过程中,学生必须具有扎实的基础知识。在此条件下,教師应训练学生的推理能力,提升其核心素养。数学推理能力不是凭空出现的,不可一蹴而就,它正是在数学基础知识上发展起来的,通过不断地训练,总结提升,方能达到预期效果。在中考复习过程中,“最短路径问题”是轴对称性质、三角形、两点之间线段最短及勾股定理计算等知识的延续和深化,对解决数学综合问题起到基础性作用。本文以一些典型的教学片段进行例谈。
1.注重思维启发,培养推理意识
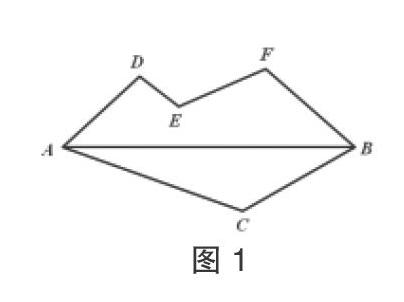
问题1:如图1,从A地到B地有三条路可供选择,你认为哪条路距离最短?说说你的理由。
师:这个问题答案是选哪个?
生:AB。
师:为什么是AB最短?
生:两点之间,线段最短。
师:很好,这个问题熟悉吗?
生:熟悉。
师:好的,那以这个问题为基础,我们学习与它有关的另一个知识,大家有兴趣吗?
生:有。
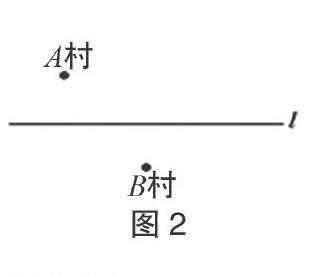
问题2:如图2,要在燃气管道,上修建一个泵站,分别向A、B两村供气,泵站修在管道的什么地方,可使所用的输气管线最短?
师:这个问题与第1个题目有联系和区别吗?
生:有,既有联系也有区别。
师:具体说一下。
生:两个问题都用到了“两点之间,线段最短”。不同的是,问题2的A、B两点分布在直线l的两侧。
师:很好,大家审题细致,那么怎么解题呢?
生:只要连接AB两点,直线l与AB的交点就是泵站修的位置。
师:大家很棒,那我们有信心做好接下来的问题吗?
生:有。
问题3:相传,古希腊有一位学者海伦,有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:“从A地出发,到一条笔直的河边饮马,然后到B地,请问到河边什么地方饮马可使他所走的路线全程最短?”这个问题对于既是物理学家也是数学家的海伦来说根本不算难题,他稍加思索,利用轴对称的知识回答了这个问题。这个问题后来被称为“将军饮马问题”。
师:这个问题与以上两题有联系吗?
生:好像有。
师:请大家一起探究,将A、B两地抽象为两个点,将河流抽象为一条直线l,在直线,上找到一点C,使AC与BC的和最小。各组同学可以围绕这个问题进行深入讨论。
显然大部分同学思维卡住了,教师顺势引出下一问题。
问题4:如图3,点A、B在直线l的同侧,在直线l上找到一点C,使AC与BC的和最小。
学生独立思考,尝试画图,相互交流。
教师提示:(1)如果点B与点A在直线l的异侧,如何在直线,上找到一点C,使AC与BC的和最小?
(2)现在点B与点A在同侧,能否将点B移到l的另一侧点B'处,且满足直线l上的任意一点C,都能保持CB=CB'?
(3)你能根据轴对称的知识,找到(2)中符合条件的点B'吗?
如图4,出示作法:(1)作点B关于直线l的对称点B';(2)连接AB',与直线l相交于点C,点C即所求。
证明:如图5,在直线l上任取一点C'(与点C不重合),连接AC'、BC'、B'C.
由轴对称的性质知,BC=B'C,BC'=B'C'.
∴AC+BC二AC+B'C=AB',AC'+BC'=AC'+B'C'.
在△AB'C'中,AB'
即AC+BC最短
师:证明AC+BC最短时,为什么要在直线l上任取一点C'(与点C不重合)?
教学反思:让学生体会作法的合理性、正确性,通过以上问题和证明方法的讲解分析,启发学生思考,潜移默化中培养学生的思维意识。教师在设计问题时,运用“两点之间线段最短”的性质将问题转化,使学生在观察实验、猜测证明的活动中养成思考的习惯。
2.注重变式训练,发展推理能力
通过学习核心知识,强化变式训练,有利于帮助学生理解数学思想和掌握数学方法,达到触类旁通的学习效果,把学习简单的知识上升到提升数学素养的层次;同时有利于培养学生的思考习惯,提高推理能力,提高解决问题的能力。
变式1:如图6,牧马营地在点P处,每天牧马人要赶着马群先到草地a上吃草,再到河边b饮水,最后回到营地,请你设计一条放牧路线,使其所走的总路程最短,并说明理由。
变式2:如图7,C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地a某一处牧马,再到河边b饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
变式3:如图8,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、E、F分别是边AB、BC、AC上的动点,则DE+EF+FD的最小值为________.
变式4:如图9,已知点A(1,-3)、点B(4,-1)、點P(a,0)、点M(a+2,0),当四边形PABM的周长最小时,a=_____.
教学反思:变式1与变式2的设计,在于帮助学生对本课内容的理解实现由表及里、从方法到思想的提升。变式3、4是为巩固对最短路径问题掌握情况而设计的,表面看变式3、4与最短路径问题不太一样,但深入探究发现,核心知识是相同的。比如在变式4中,路径AB是固定的,可先不考虑,而PM能转化为一条固定方向和长度的线段。在解答变式题3、4时,若思维止于表面,那么将无法与轴对称变换联系,思路将无法形成。
3.注重改编设题,提升思维素养
学生完全自编题目当然有很大困难,但如果改编就容易多了,学生可以试着改变问题的背景,改变问题的条件,改变问题的结论或改变问题的类型。如果教师在设计问题时就注重问题的开放式设计,那么学生改编题目就有了参照,对于激发学生的兴趣,发展逻辑思维能力有很大的帮助。
例如:以变式3为母题,启发学生改变问题的呈现背景,把三角形问题改为矩形问题,如图10,矩形ABCD中,AB=3,BC=4,E、F、G分别是AB、BC和对角线AC上的点,则GE+EF+FG的最小值为( ).
教学反思:在数学问题的改编中,教师应该尝试给学生思考的机会,引导学生抓住问题的关键因素展开联想,变化出更多样的图形。教师在教学设计中的编题设计环节对学生限制少一些,让学生有更多的自主权去增加新的条件,从解题人向出题人转变,跳出思维定式,充分发展逻辑推理能力;将学生设计的题目展示给大家评议。通过评议,学生精准读懂编题者的设计意图,更容易形成思维路径,提高逻辑推理能力,形成解答思路,同时也可以增强学生编题的积极性和自豪感。
【参考文献】
[1]王小莉.化归思想在中学数学教学中的渗透——以《最短路径问题》为例[J].教育现代化,2018(10):350-352.

