螺旋桨流激噪声与泄涡频率关系分析

杨振宇，姚慧岚，张怀新

（上海交通大学 高新船舶与深海开发装备协同创新中心，上海 200240）

0 引 言

螺旋桨振动是舰船的主要噪声源之一，尤其是当桨后涡脱落的频率与桨的某阶固有频率接近时，可能会产生共振，严重时会引发“唱音”现象。流激振动引起的流激噪声和“唱音”现象会对船舶的正常运行产生影响。尤其是近年来，随着新型复合材料的不断发展，螺旋桨的材质及其固有属性不断发生变化，准确预测螺旋桨“唱音”的发生变得越来越困难。因此，研究一种可在设计阶段对螺旋桨“唱音”现象进行预报的数值方法至关重要。对于普通船舶而言，螺旋桨“唱音”不仅会破坏船舶的舒适性，影响船上工作人员的工作效率和身心健康等，而且可能会破坏海洋生物的生存环境；共振容易造成螺旋桨桨叶出现结构疲劳，导致螺旋桨的使用寿命变短。对于潜艇和军舰而言，对“唱音”进行研究更为重要，因为潜艇对隐蔽性的要求很高，而“唱音”的产生会导致其隐蔽性变差。在当前的船舶技术中，一旦出现“唱音”现象，会通过对螺旋桨进行简单处理来避开，如对桨叶进行削薄或对其形状进行微调处理等，大多数情况下会使“唱音”现象有所改善，但并没有较为显性的数值判断，且后期可能会影响螺旋桨初始的设计参数。因此，目前并没有比较好的能在设计阶段就预测并避免“唱音”现象出现的方法。

目前国内外已有一些关于螺旋桨流激噪声和“唱音”的研究。例如：DAPENG 等[1]通过对信号时间序列进行研究，重构螺旋桨“唱音”系统，为进一步研究螺旋桨“唱音”现象提供了新的途径；李洁雅等[2]认为引发“唱音”现象的主要原因是桨叶随边旋涡的频率恰好与桨叶的固有频率接近，并提出了解决该问题的方法；杜宜洋[3]对单个桨叶进行了旋涡发放研究和频响分析；马骏等[4]通过建立螺旋桨水中流体与固体耦合振动方程来研究螺旋桨涡激诱发的振动响应的计算方法；刘晓宙等[5]采用Lighthill 声比拟方法研究机翼涡激振动引起的声辐射，发现当涡脱频率与机翼的固有振动频率一致时，会出现锁定现象，此时的声辐射达到最大。另外，很多学者提出或应用了一些声学计算方法。例如：吴思远[6]采用间接边界元法计算了桨叶的辐射声功率、声辐射效率和场点声压，并对声功率和桨叶固有频率的相关性进行了分析；卢云涛等[7]应用FW-H 声学模型（The Ffowcs Williams and Hawkings Model），通过非定常计算模拟了潜艇流噪声声场；刘志龙[8]以非定常脉动压力为噪声源，结合声学无限元方法计算了复合材料螺旋桨的振动声辐射特性；鲁利等[9]分别将采用RANS、DES 和LES 等3种方法得到的脉动压力作为声源，结合声学边界元预报辐射噪声，提供了预报噪声时选择湍流方法的依据；YAO 等[10]采用LES 方法和声学边界元方法对潜艇的水动力噪声和流激噪声进行了比较研究；李燎原[11]采用有限元/边界元方法研究了不同轴系校中状态下船体结构振动及其水下辐射噪声的差异；李环等[12]对在航行体水动力噪声工程预报方面有较好应用前景的声类比法、黏声分离法和声边界条件法等3种方法进行了比较。

综合来看，国内外以螺旋桨整体为研究对象，探究流激振动引起的噪声和“唱音”现象与泄涡频率相结合的研究相对较少。大部分关于流激噪声的研究主要集中在对简化之后的螺旋桨单桨叶或水翼进行数值计算，或根据实际经验给出通过修改桨叶来避免“唱音”的方法，但对预测“唱音”方法的研究还不多，从设计阶段解决“唱音”问题的办法尚未形成。考虑到目前船舶的舒适性越来越受重视，尤其考虑到潜艇和舰船等的隐蔽性需求，本文对流激振动引起的“唱音”现象进行分析，所得结果对数值预报“唱音”现象有一定的参考意义。

本文在计算螺旋桨的瞬态流场时，通过利用自定义函数监测螺旋桨随边附近的压力变化，得到泄涡频率。通过微调节螺旋桨材质的杨氏模量，使螺旋桨的固有模态发生改变，从而使螺旋桨的某阶模态振动频率与泄涡频率接近，以研究其对螺旋桨附近声场的影响，对其引起的流激噪声进行详细分析，并进一步推测引起螺旋桨出现“唱音”现象的原因。潘雨村[13]研究认为低频段一般与螺旋桨轴频和叶频有关，因此本文着重研究泄涡频率的高频段可能出现的共振现象，从而减少螺旋桨设计中共振（乃至“唱音”）现象的出现。

1 物理模型和网格划分

本文以波茨坦螺旋桨算例[14]（Potsdam Propeller Test Case, PPTC）为研究对象。PPTC 桨作为算例桨，在2011年于德国汉堡举办的船舶推进器国际会议（International Symposium on Marine Propulsors, SMP）的相关研究报告中提出，其主要参数见表1。

表1 螺旋桨主要参数

图1 为螺旋桨流场分布图。选择在螺旋桨上游2D（D为模型螺旋桨直径，0.25m）处设置其来流的进口；选择在螺旋桨下游10D处设置螺旋桨流场区域的出口；选择直径为10D的整个圆柱（实线区域内）作为计算域。计算域分为旋转域和静止域，其中：旋转域（虚线区域内）的直径为2D；旋转域外部为静止域。速度入口均匀来流；出口为压力出口，设置为0Pa。螺旋桨的转速为900r/min。瞬态计算时间步长为5×10-5s。

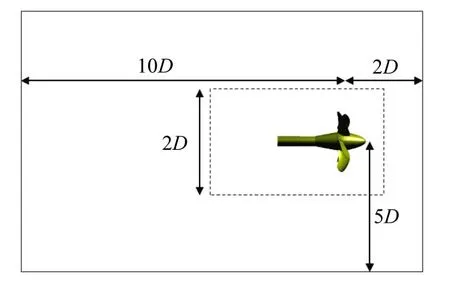
图1 螺旋桨流场分布图

本文在划分网格时采用非结构四面体网格，为准确捕捉桨叶的泄涡，在桨叶的随边、导边、叶根和叶梢等部位进行局部加密，网格数量约为330 万个。

2 数值方法

2.1 流场求解方程

本文采用计算流体力学（Computational Fluid Dynamics, CFD）软件FLUENT 进行流场求解。由于需获得桨叶随边较为清晰的泄涡情况和尽量减少计算量，本文采用Menter F R 提出的k-ωSST 两方程湍流模型[14]。该模型既保留了近壁面的k-ω模型，又保留了远壁面的k-ε模型，可较好地兼顾远离壁面时湍流流动的情况和复杂压力梯度下的边界层情况。流动方程为

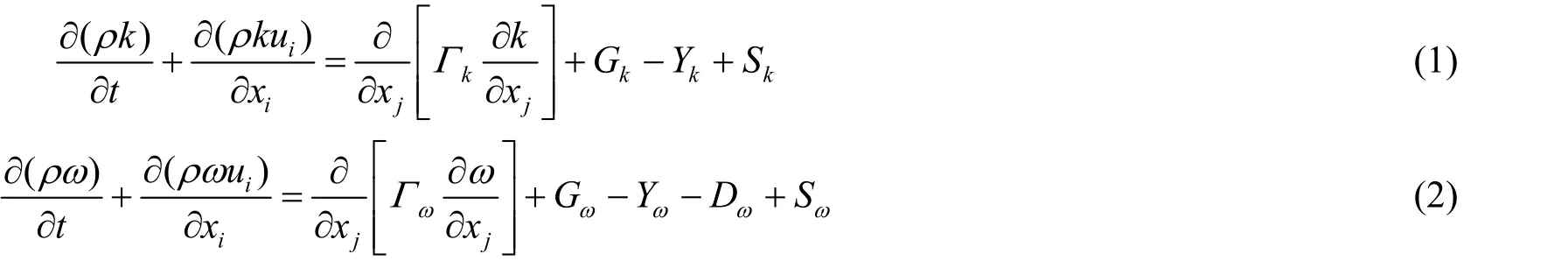
式(1)和式(2)中：kG为湍流的动能；Gω为ω的方程；kΓ和ωΓ分别为k和ω的有效扩散项；kY和Yω分别为k和ω的发散项；Dω为正交发散项；Sk和Sω为自定义系数。

2.2 噪声求解方程

本文采用软件Virtual.Lab 进行噪声求解；采用边界元理论进行声场求解。整体思想是将空间型问题转化为边界型问题。声场中点的计算式为

式(3)中：p(x) 为声场中任一点的声压；p(y) 为声源点的声压，这里声源是前面流场计算得到的螺旋桨表面脉动压力；α(x)为曲面光滑系数；为声源边界与媒介交界处的法向速度，这里指螺旋桨流激振动引起的表面法向速度。式(3)中G(x,y) 的计算式为

同FW-H 方程相比，边界元方法的优势体现在：

1) 边界元方法是一种降维方法，体网格变为面网格，网格数量锐减，从而提高计算效率；

2) 边界元方法是一种直接频域计算方法，与时域方法相比，能提供更多的信息；

3) FW-H 方程常用来计算远声场，因此本文的噪声计算采用边界元方法，可更好地表现近声场和远声场。

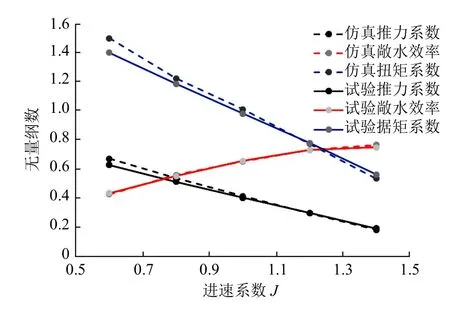
图2 螺旋桨敞水性能数值模拟结果与试验结果对比

3 网格的验证

螺旋桨敞水性能数值模拟结果与试验结果对比见图2。从图2 中可看出，当J在0.6～1.4 范围内时，各项误差并不大，尤其是在一般的设计工况下（即J≈1.2时），精确度最高。因此，后续基于J=1.2（即来流速度为4.5m/s）时得到的桨叶压力数据进行计算。本文采用的几何模型和网格划分方法经验证都是比较合理的，得到的敞水螺旋桨桨叶压力分布和泄涡情况可为后续振动和噪声分析所用。

4 泄涡频率分析

由于泄涡的形态主要出现在桨叶的随边附近，且泄涡的产生与压力变化直接相关，因此本文通过监测桨叶随边附近监测点的压力变化来判断泄涡的变化。选取随边上从0.6r（r为桨半径）处到叶梢的一系列点进行压力监测。监测的方式是，采用FLUENT 软件对螺旋桨进行瞬态计算，时间步长设置为5×10-5s，并设置为动网格，通过加载自定义函数，使监测点随着桨叶的转动而转动，在每个时间步输出桨叶监测点的压力，由此得到一系列监测点的压力变化数据。

由于多数监测点的压力变化情况差别不大，选取具有代表性的0.95r附近随边监测点的压力变化情况进行分析（见图3）。由图3 可知，监测点的压力呈周期性变化，周期约为0.013s。由于螺旋桨的转速为900r/min，因此轴频为15Hz，而该桨为五叶桨，叶频为75Hz，周期为0.013s，与监测点压力周期基本一致。

对监测点压力进行傅里叶变换，得到监测点压力频域图见图4。由于高阶频率幅值较小，因此将图4中的频率范围拆分为0～300Hz 和100～3000Hz，得到监测点压力频域图见图5 和图6。这样可更清晰地看到全范围频域的特性。由图5 可知，在60Hz 和120Hz 等低频区域有峰值出现，这些频率均为倍轴频，本文不对这些低频区域的频率做更深入的研究。由图6 可知，在1700Hz 和2600Hz 等高频区域附近有一些高频幅值线谱出现。

高频幅值频率极有可能与泄涡频率相近，因此约在1767Hz 和2612Hz 附近形成了高频幅值区域。该情况与姚慧岚等[15]研究得到的螺旋桨泄涡频率附近有多条线谱的结论一致，因此判断这2 个区域为接近泄涡频率的区域。由于泄涡的成分比较复杂，其中可能包含大小涡，因此出现2 个高频幅值区域是可能的。

通过分析可知，本文采用的螺旋桨模型在均匀来流速度为4.5m/s、转速为900r/min 时，其泄涡频率约为1767Hz 和2612Hz。

图3 0.95r 随边监测点压力变化

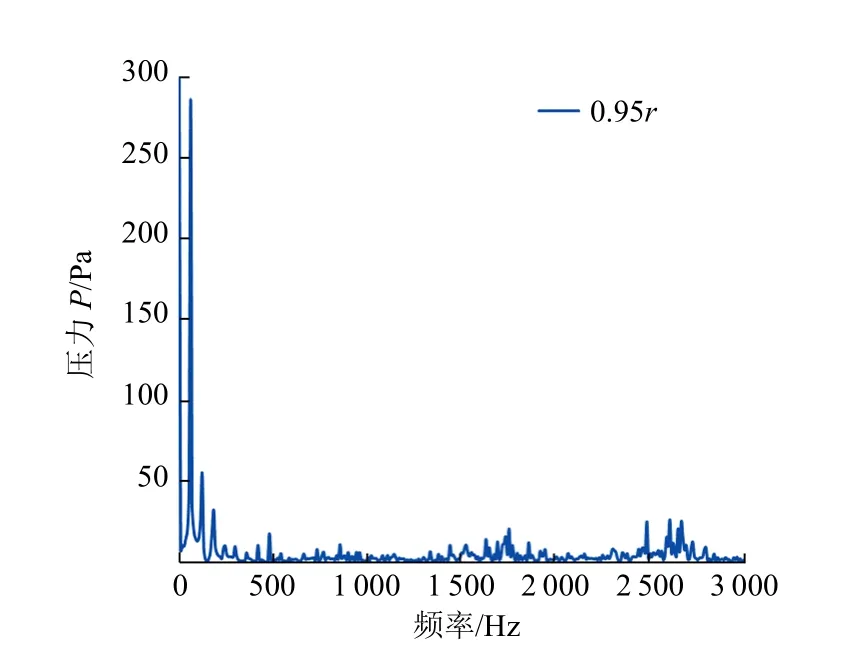
图4 监测点压力频域图

图5 监测点压力频域图（0～300 Hz）

图6 监测点压力频域图（100～3000 Hz）

5 模态分析

随着新型复合材料的出现和发展，其特性逐渐发生变化，这里假设材料的变化使得杨氏模量发生变化，进而导致螺旋桨的模态发生变化。材料1 采用结构钢（密度ρ=7850kg/m3，杨氏模量e=1.907×1011，泊松比μ=0.3）；材料2 采用某假设的复合材料（密度ρ=7850kg/m3，杨氏模量e=2.3×1011，泊松比μ=0.3）。由于这里材料密度对数值计算结果无明显影响，因此只调整杨氏模量，使得螺旋桨的某阶模态接近螺旋桨的泄涡频率。由于泄涡频率在3000Hz 以内，因此这里只考虑3000Hz 以下的各阶模态频率。利用ANSYS软件分析螺旋桨在2种材料下的各阶模态频率，结果见表2。

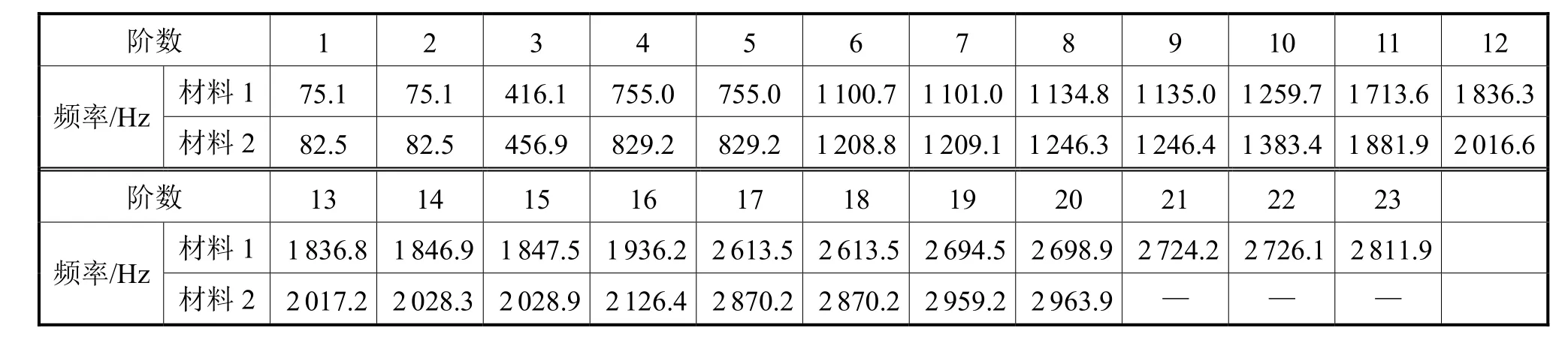
表2 螺旋桨泄涡频率小于3000Hz 时的1～23 阶干模态频率

由表2 可知：材料1 的11 阶模态频率1713.6Hz 与泄涡频率1767Hz 十分接近，17 阶模态频率2613.5Hz与泄涡频率2612.0Hz 十分接近，此时极有可能会发生共振，从而引起噪声增大，严重时可能会引发“唱音”现象；材料2 的各阶模态频率均与泄涡频率远离，推测应该没有引发共振现象。

6 流激噪声分析

采用Virtual.Lab 软件的间接边界元方法进行流激噪声分析。通过FLUENT 瞬态流场计算得到桨叶cgns格式的压力数据文件，将其导入到Virtual.Lab 中计算出螺旋桨的位移，将该位移转移到声学面网格上即可得到声学的位移边界条件，从而可求解出各监测点的声学信息。

6.1 声压级监测点的分布

在螺旋桨的轴向和径向各布置1 个点（见图7 中的圆点），其中：轴向监测点距离中心点2D；径向监测点在以中心点为圆点，以D为半径的圆上。声压云图采用过螺旋桨桨叶中心原点并垂直于桨轴的正方形平面，边长为4D，切分成20×20 个网格（见图7 中的网格区域）。声指向性图是以螺旋桨中心点为圆心，以4D为半径的平行于桨盘面的圆。为对比2种材料的声学特性，其监测点均取在相同的位置。

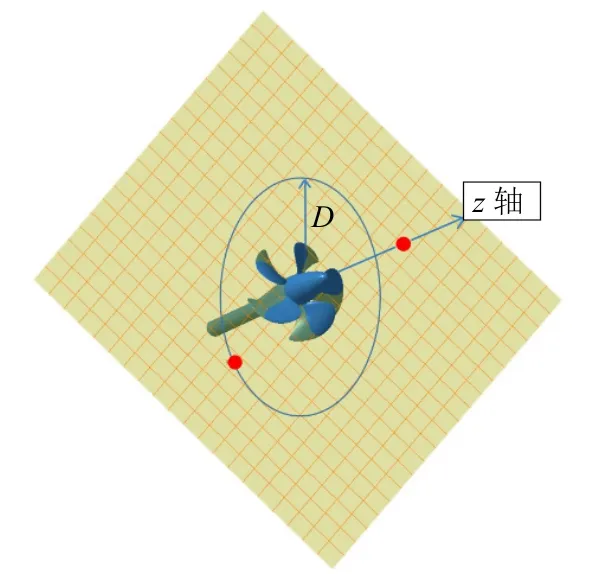
图7 监测点分布图

6.2 振动位移分析

图8 和图9 为2种材料螺旋桨在泄涡频率为1760Hz 时的振动位移云图。由图8 和图9 可知，材料1 螺旋桨的振动位移较大。对于材料1 螺旋桨，其11 阶模态频率1713.6Hz 与泄涡频率十分接近时，振动幅值最大为0.000043mm；对于材料2 螺旋桨，在同一频率1760Hz 下，当各阶模态固有频率远离泄涡频率时，振动幅值最大为0.000087 mm。显然，材料1 螺旋桨的振动幅值远大于材料2 螺旋桨，因此可判断此时材料1 螺旋桨在1760Hz 附近与泄涡频率发生了共振。同理可得2种材料螺旋桨在泄涡频率为2612Hz 时的振动位移见图10 和图11。

图8 泄涡频率为1760 Hz 时材料1 螺旋桨振动位移

图9 泄涡频率为1760 Hz 时材料2 螺旋桨振动位移

图10 泄涡频率为2620 Hz 时材料1 螺旋桨振动位移

图11 泄涡频率为2620 Hz 时材料2 螺旋桨振动位移

6.3 点声压频谱图分析

图12 为杨氏模量不同时轴向监测点的声压频谱比较。从图12 中可看出，在2 个泄涡频率区域附近，材料1 螺旋桨的声压级要比材料2 螺旋桨的声压级高20dB 左右，而这2 个频率分别对应于材料1 螺旋桨的11 阶模态频率和17 阶模态频率，因此可推测，此时材料1 螺旋桨的11 阶模态频率和17 阶模态频率与泄涡频率相近导致共振发生，从而导致噪声增大20dB 左右。对于其他频率点，2种材料螺旋桨的声压级相差不明显。综上，可推测当泄涡频率与螺旋桨固有模态相近时，流激振动可能导致较大的流激噪声。

同样，对于径向监测点（见图13），在泄涡频率附近出现了明显的材料1 螺旋桨的声压级比材料2 螺旋桨的声压级高约20dB，而在其他区域不是特别明显（少数点有些异常，可能是由于径向监测点位置的选择没有轴向监测点对称均匀地受各桨叶振动的影响），由此验证了上述结论。

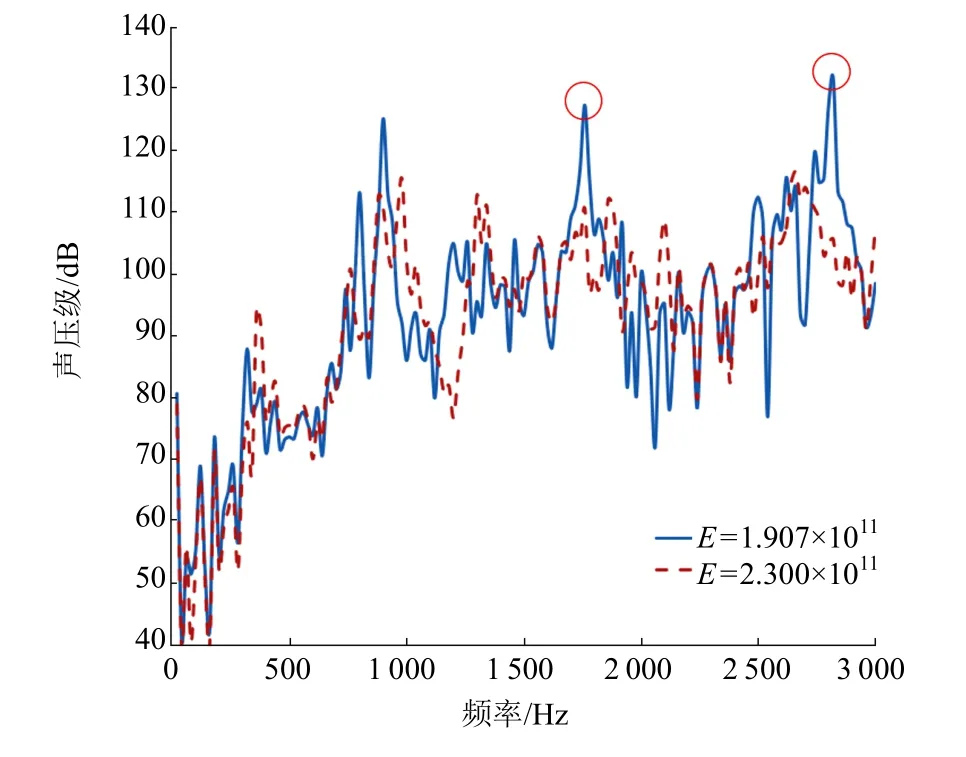
图12 杨氏模量不同时轴向监测点的声压频谱比较

图13 杨氏模量不同时径向监测点的声压频谱比较

6.4 声压云图分析

图14 和图15 分别为1760Hz 泄涡频率处材料1 螺旋桨和材料2 螺旋桨的声压云图。由图14 和图15可知，材料1 螺旋桨的声压的最大值明显大于材料2 螺旋桨（高出约40dB），且总体上普遍高于材料2 螺旋桨，而该频率同样接近泄涡频率。同理可得泄涡频率为2620Hz 时材料1 螺旋桨和材料2 螺旋桨的声压云图（分别见图16 和图17）。由此可见，螺旋桨某些阶次的固有模态频率与泄涡频率相近时可能会导致共振发生，严重时可能导致“唱音”现象出现。

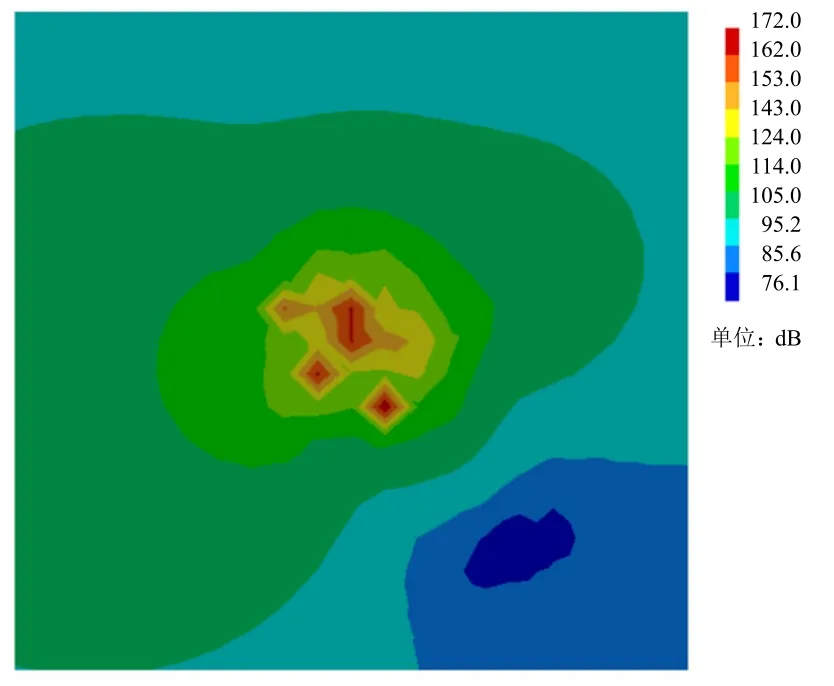
图14 泄涡频率为1760 Hz 时材料1 螺旋桨声压云图

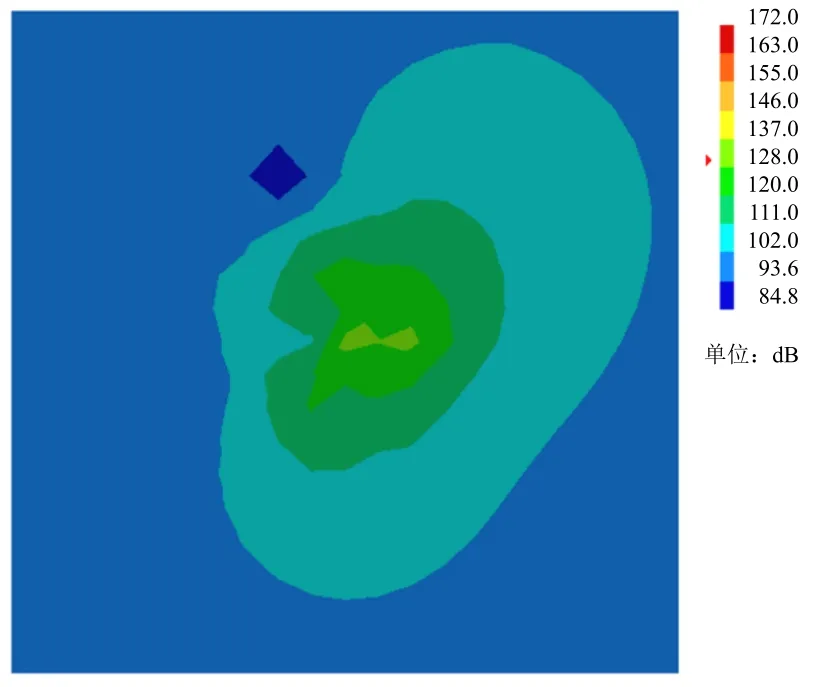
图15 泄涡频率为1760 Hz 时材料2 螺旋桨声压云图

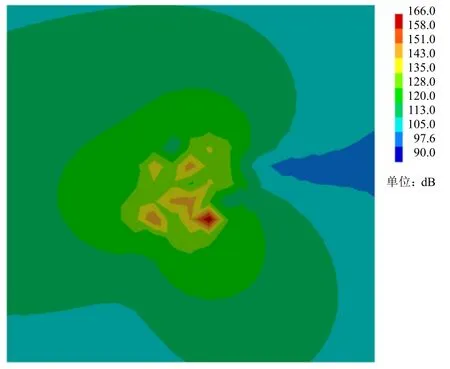
图16 泄涡频率为2620 Hz 时材料1 螺旋桨声压云图

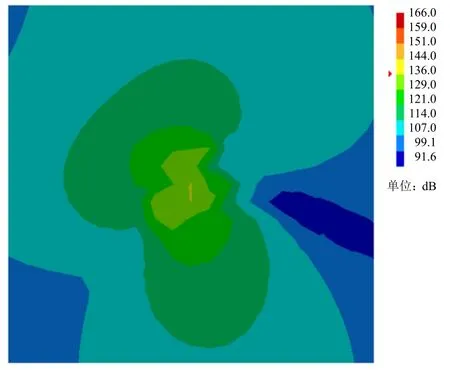
图17 泄涡频率为2620 Hz 时材料2 螺旋桨声压云图

综上可知：当螺旋桨的某阶模态频率与泄涡频率接近时，流激振动发生共振，使得流激噪声增大；当二者极其接近时，可能会引发“唱音”现象。

7 结 语

本文通过调节螺旋桨材质的杨氏模量来改变螺旋桨的模态特性，使之接近泄涡频率，研究泄涡频率是否会因与螺旋桨自身产生共振而引发“唱音”现象，进而研究其声场特性。

1) 当螺旋桨某阶模态的固有频率与泄涡频率相近时，结构会发生共振，导致流激噪声增大。噪声的增大等级可能与频率相近程度有关。

2) 当螺旋桨的某阶模态频率与泄涡频率极其接近时，可能会导致“唱音”现象出现。

3) 在设计阶段，应通过数值模拟得出螺旋桨泄涡频率和各阶模态频率，并尽量改善螺旋桨的几何设计或材料使用，使两者避开。

4) 预先进行数值模拟可得到相应的各阶模态，各阶模态受杨氏模量的影响很大，可根据需求开发新型螺旋桨复合材料。

5) 本文研究的频域范围相对较小，通过改变杨氏模量来调节固有频率的方法较为单一。未来将对改变螺旋桨随边的切面形状克服“唱音”的作用机理等更多方向进行研究。