海上风电场桩基的水动力特性
谢启迪,张美满,包雄关
(1. 宁波天一海运有限公司,浙江 宁波 315000;2. 宁波大学 海运学院,浙江 宁波 315000)
0 引 言
海上风电场因具有风资源可利用时间长、风功率密度大、湍流小、零排放和距离负荷中心近等优点而得到越来越多国家的关注。由于海上风电场不可避免地与航道、渔场等毗邻甚至相互穿插,风机基础存在与船舶(尤其是靠近风电场作业的运维船和渔船等小型船舶)撞击的风险。一旦有超过防撞标准的船舶撞击风机桩基,会造成风机桩基局部受损甚至倒塌,给风电场投资方带来损失并可能产生一定的社会影响。因此,对海上风机的水动力特性进行探究具有重要意义。本文通过OpenFOAM 仿真软件准确反馈风机指定区域的流场信息,根据不同工况下的流场信息,有选择地实施通航管理措施、预警措施和防船撞防护措施,为海上风机防撞研究提供参考。
PRSIC 等[1]运用OpenFOAM 软件的Smagorinsky 子网格规模模型进行了大涡模拟,结果表明,在不同自由跨度下,海洋管道周围的三维流动均不同。石世杰[2]利用OpenFOAM 软件对空气动力学课程教学中常见的流动问题进行求解,得到了圆柱绕流计算分析、翼型气动性能分析和层流分离及转捩现象分析的计算结果。湛俊华[3]基于OpenFOAM 软件对雷诺数为3900 时的三维固定圆柱绕流和雷诺数为30000时的三维圆柱受迫振动进行了数值模拟,得到的阻力平均系数能与试验值较好地吻合。蘧鑫晨[4]采用有限体积法求解不可压缩Navier-Stokes 方程,开展了不同雷诺数下的三维圆柱绕流流场数值模拟研究。
BOUZARI 等[5]采用OpenFOAM 软件研究了添加直翅片对瞬态热和圆柱体上流动的流体热力和水力特性的影响。端木玉等[6]基于OpenFOAM 软件的大涡模拟方法,以连续方程和Navier-Stokes 方程作为控制方程,选用Smagorinsky 模式为亚格子应力模型,对雷诺数为3900 时的三维圆柱绕流问题进行了数值模拟研究,并着重分析了其尾流的特征和性质。赵骥等[7]针对Navier-Stokes 方程,根据Helmholtz 速度分解,将流场速度分解为势流部分和非势流部分,剥离势流部分之后得到了黏势流耦合的变形N-S 方程,并在OpenFOAM 平台内实现了变形N-S 方程的黏势流耦合计算。KESKINEN 等[8]采用3种LES(Large Eddy Simulation)模型在轴对称活塞-缸体几何结构中进行了大涡模拟,3种LES 模型对流量统计的敏感性不同。
王力[9]基于OpenFOAM 开源计算软件,通过对网格进行参数化控制,快速生成了较好的网格,探讨了层流条件下不同雷诺数圆柱绕流的阻力系数Cd、升力系数Cl、斯特罗哈数St。STRINGER 等[10]采用ANSYS和OpenFOAM 软件开源求解器设计了一种计算圆柱体周围流动的方法,并对其有效性进行了测试。刘强[11]对不同雷诺数下的圆柱绕流进行了数值模拟,探讨了LES 模型和Spalart-Allmaras 一方程模型这2种湍流模型的具体应用,计算得到的阻力系数和斯特罗哈数与试验结果具有良好的一致性。
1 数学模型
圆柱绕流流态与雷诺数有关,桥墩绕流一般处于极超临界区内,属于湍流流态。根据已有的研究成果,水流运动应满足质量守恒、动量守恒和能量守恒。本文采用笛卡尔坐标系计算,在该坐标系内,基本方程表示如下。
1) 不可压流体连续性方程

2) 运动方程
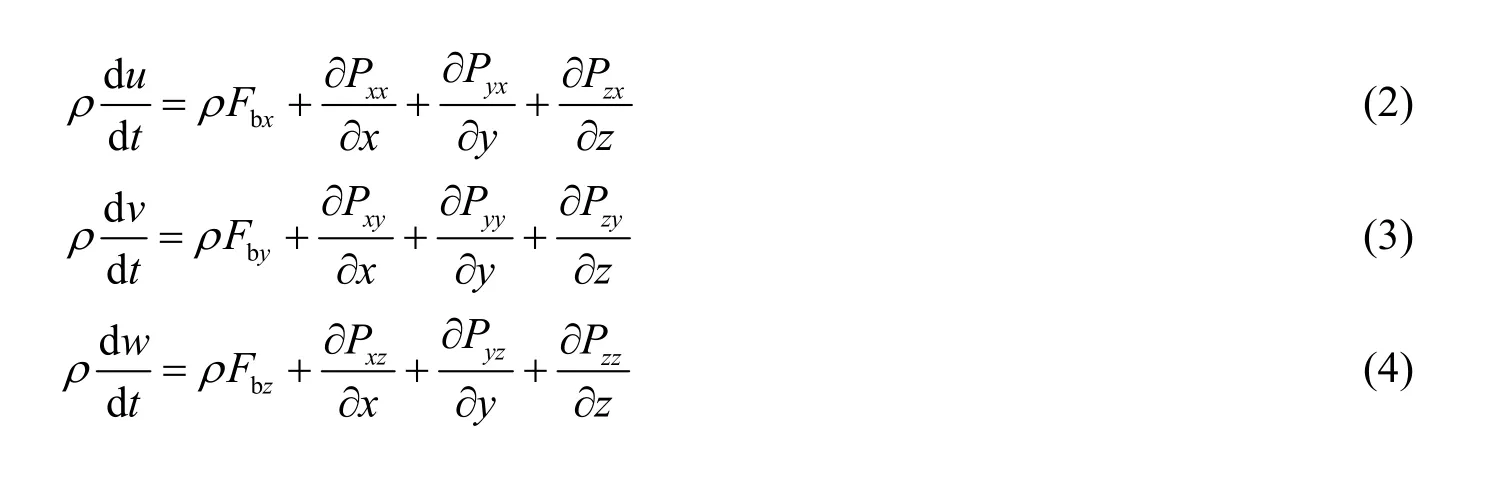
式(1)~式(4)中:Fbx、Fby和Fbz分别为作用在一个单位质量流体上的质量力沿x、y和z等3 个方向的分量;Pij为流体内应力张量的分量。
本文采用湍流模型模拟二维圆柱绕流。RNGk-ε模型基于标准k-ε模型,修正了湍流黏度,考虑了平均流动中的旋转和旋流流动,并在ε方程中添加了附加项,比标准k-ε模型更适合模拟圆柱绕流场。
RNGk-ε模型中的湍动能方程和耗散率方程的表达式如下。
1) 湍动能方程
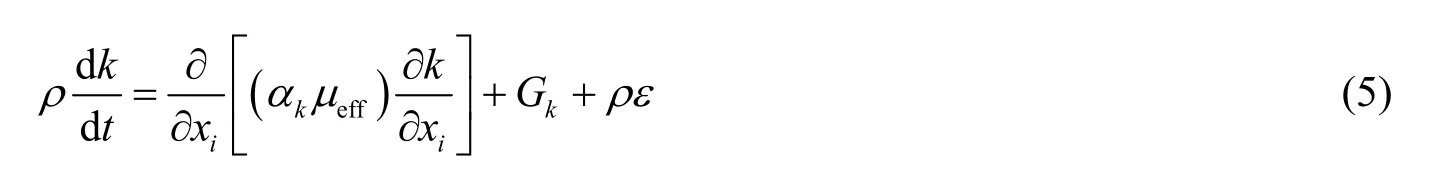
2) 耗散率方程

式(5)和式(6)中:k为湍流动能;ε为湍流耗散率;kG为湍动能产生项,为有效黏度,为流体的动力黏性系数;tμ为湍动黏度,
OpenFOAM 采用有限体积法离散控制方程,适用于结构化网格和非结构化网格。将求解域划分为一系列网格,计算节点布置在网格中心。本文选用的OpenFOAM 版本为6.0,在Linux 系统下运行。选用的Linux系统版本为Ubuntu 18.04。
2 研究对象
本文所述单圆柱绕流模型(见图1)的计算域是二维的,由一个长30m、宽10m 的长方形和一个直径为1m 的圆组成,该长方形计算区域的实际大小为30m×10m,水流方向自左向右。水流从进口边界流入,从出口边界流出,上下两侧分别是顶层边界和底层边界。
由于风机基础构件较为复杂,直接使用 blockMeshDict 进行几何定义会因顶点较多而导致建模复杂。因此,本文采用第三方软件ICEM 进行仿真模拟,将其简化为一个直径为1.0m 的圆柱体(见图2)。

图1 二维圆柱绕流模型

图2 采用ICEM 生成的圆柱模型
3 预处理和后处理
采用blockMesh 生成背景网格;修改blockMeshDict 字典文件,改变圆柱中心坐标(23.5, 10.0, 0.0)。生成背景网格之后,采用OpenFOAM 自带的网格划分工具extrudeMeshDict 实现网格划分。通过foamGet 指令拷贝extrudeMeshDict 字典文件之后,修改该字典文件执行extrudeMesh 命令和checkMesh,最终得到圆柱的二维绕流模型图和网格图(见图3)。由于结构网格在面对复杂几何外形时生成困难,故对海上风电机基础部分周围采用非结构化网格,对距离风机基础较远的区域采用结构化网格,非结构化区域见图4 中的椭圆形区域。

图3 二维圆柱绕流模型的整体网格图

图4 二维圆柱绕流模型的局部网格图
4 升阻力情况分析
根据上述OpenFOAM 单圆柱仿真模型,结合实际海域的多种天气因素对边界条件进行修改,提出几种工况。修改之后,在不同雷诺数下对比已有的仿真试验数据,对单圆柱绕流的升阻力情况进行分析,结果见表1。

表1 不同雷诺数下单圆柱绕流参数
高雷诺数下的数值模拟方法有直接数值模拟(Direct Numerical Simulation, DNS)、雷诺平均方法(Reynolds Equation, RANS)、LES 和分离涡模拟(Detached-Eddy Simulation, DES)等。由表1 可知,本文的模拟结果数据与已有试验结果更吻合。当时,已有的LES 模拟结果比试验结果要小;当时,LES 模拟结果比试验结果要略大,可见其在高雷诺数下模拟方法的误差较大。本文采用改进之后的RANS 方法得到的数值更接近试验数据。因此,对于高雷诺数下的单圆柱绕流,采用改进的RANS 方法所得结果更精确。但是,由于网格划分不均匀、实际流场环境复杂和流速发生跃变等问题的存在,计算结果仍存在一定的误差。
图5为雷诺数为1.0×105、3.0×105和3.5×106时的升阻力系数。由图5 可知,不同雷诺数下的阻力系数有明显不同,随着雷诺数的增大而减小。阻力变化虽然有波峰和波谷,但在不同雷诺数下其幅值基本上相同,周期性并不明显,变化趋势不平缓,基本变化为起初周期短,中期周期长,后期周期回归到初始时的大小。此外,从图5 中还可看出不同雷诺数下单圆柱的升力均值为 0,在流动稳定之后,升力系数呈现周期性变化规律,但不明显。
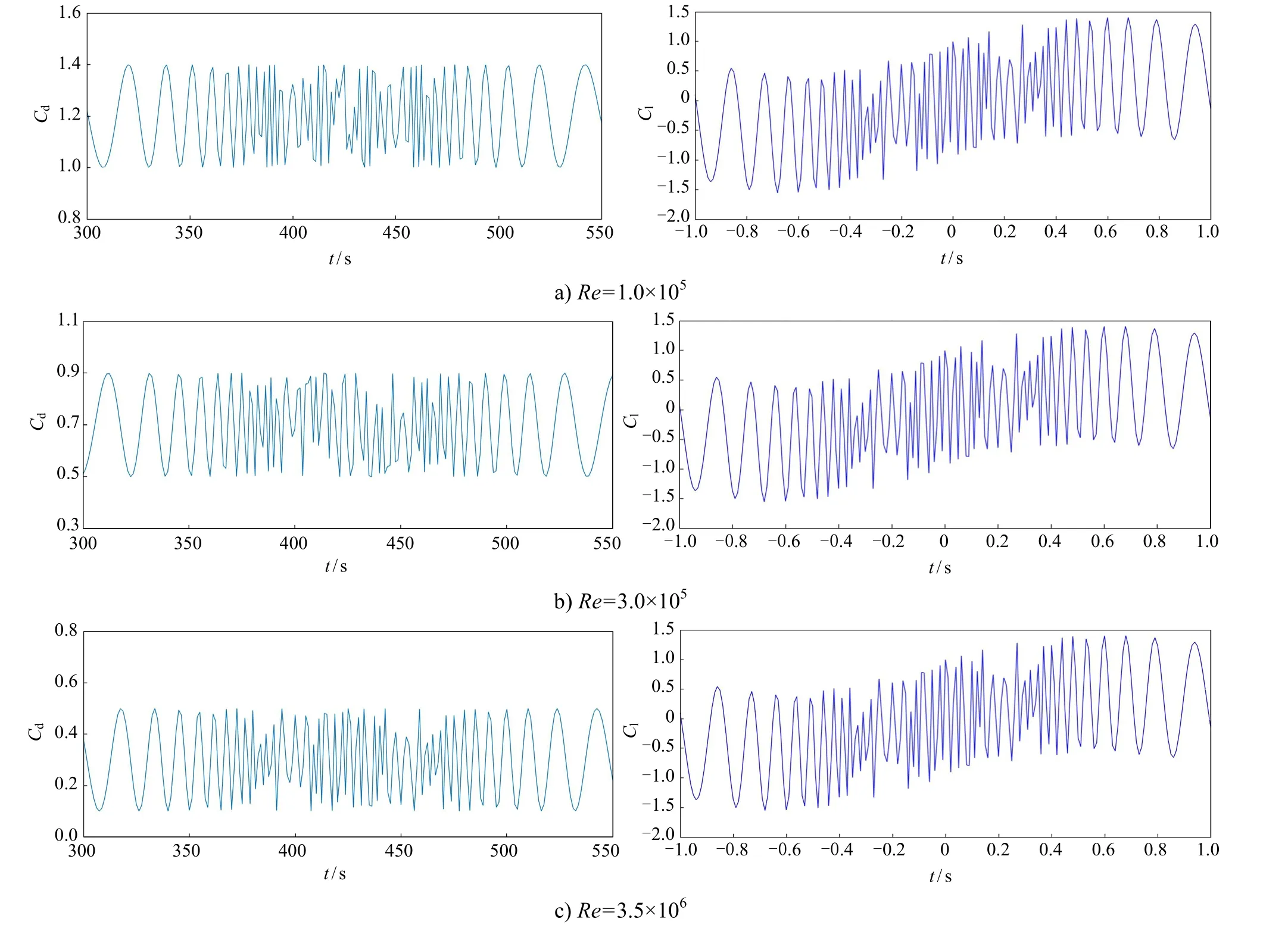
图5 不同雷诺数下圆柱的升阻力系数变化曲线
5 流场分析
在本文所述单圆柱绕流案例中,随着Re的增大,涡旋结构逐渐产生(见图6)。但是,在Re达到3.5×106时,涡旋会减少。不同时刻圆柱对水流特性的影响不同,风机基础和该结构前端的尾流结构均与时间有关。随着时间的增加,圆柱周围的流速呈现出减速的尾流带,尾流流速明显增大,其尾流结构的范围比前侧尾流结构的范围要小。
流速U在风机基础前端开始减小,在后侧随前侧一起减小,前侧和后侧出现的低速区范围基本上相同。风机基础两侧发生绕流,出现明显的流速缓冲带,并向上游延伸。然而,随着雷诺数逐渐增大,圆柱绕流的流场变化越来越明显。当雷诺数增大到3.0×105时,由图6b 和图6c 可知,水流经过风机基础附近时,风机基础两侧的横向流速略微减小,并形成旋涡。柱后涡的形态不同,可看出涡在柱左侧(即来流方向)先形成,涡外延向后流动,在相反方向方形成相对的涡,相对涡的外层流线会与柱面相切,这与此时的雷诺数较大有关。

图6 不同雷诺数单圆柱绕流的流场网格和尾流形态
6 结 语
海上风电机基础对水动力特性的影响研究可为航道安全距离探究提供理论支持,是风电场水域风机防撞研究的基础。本文采用改进的RANS 模型对单圆柱的流动特性进行二维数值模拟,在不同雷诺数(1.0×105,3.0×105,7.0×105,3.5×106)下分别模拟圆柱绕流流场,主要得到以下结论:
1) 对于单圆柱绕流的阻力系数,阻力变化基本上表现为陡然增大和骤然减小,且周期性不明显。不同雷诺数下的阻力系数变化规律相似,且振幅基本上相同。当雷诺数在3.0×105与3.5×106之间时,为临界雷诺数,涡旋结构不明显,阻力系数约为1.2;随后随着雷诺数的增大,阻力系数又有所下降。单圆柱绕流的升力系数在 0附近周期性波动,幅值不是很稳定,但相差不大,不同雷诺数下的幅值变化规律不同,幅值变化范围相同。
2) 不同时刻圆柱对水流特性的影响不同,风机基础和该结构前端的尾流结构均与时间有关。随着时间的增加,圆柱周围流速呈现出减速的尾流带,尾流流速明显增大,其尾流结构的范围比前侧尾流结构的范围小。

