素数递推式——素运式

◎张国平 （福建省南平市福州大学，福建 南平 353416）

为了述说的方便，明了，现做以下规定：

PN：P表示素数，N表示素数P在素数序列中的排列位置.如素数序列：2，3，5，7，11，13，17，19，….

则PN表示 21，32，53，74，115，136，177，198，…，PN－1，PN，PN＋1，….

PN＝21推式：

［2，0］⇒2N＋0，由于在自然数中，其最小值为 0，2 是最小的素数，且是唯一的偶素数，所以在后面［2，0］不再参与推算.

PN＝32推式：［2，1］，

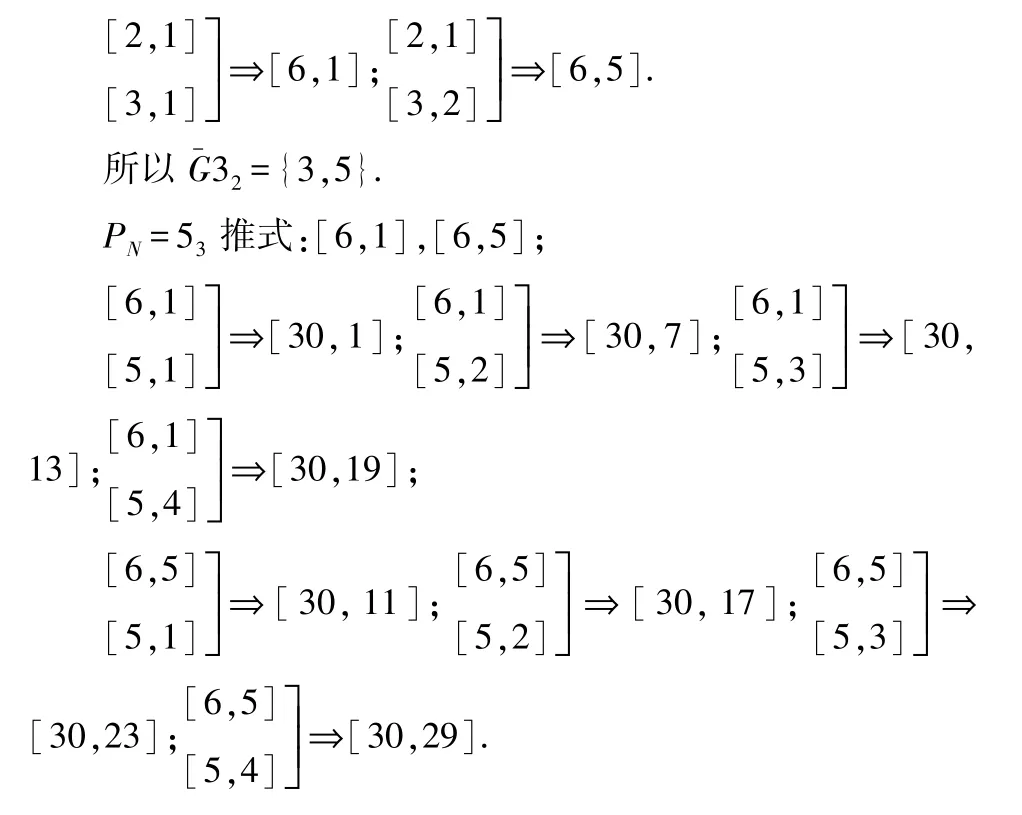
在PN＝ 74推式中，由于＝ 49，而 74的下一个素数P5＝115，故在74推式中，除1 外其最小数为其下一个素数115，即74推式中的数除1 外的最小数为74的下一个素数115，而其最大的数为 74！ －1＝209（74！ ＝2×3×5×7 ＝210）.而在74推式中，其数值小于115的平方的数必是素数，而不小于115的平方的数则有可能不是素数，但其参与下一推式的推算是必要的，否则，素数将会缺失！

由于 74的后续素数是115，136，177，198，239，….而在 74推式中且 209÷11 ＝19，故而，在74推式中：

11×11＝121；11×13＝143；11×17＝187；11×19＝209；

13×13＝169；13×17＝221＞209（舍）；

17×17＝289＞209（舍）.

一般地，当PN为第N个推式时，其最小数除1 外为PN的下一个素数PN＋1，其最大的数为PN！ －1，在中，其值若小于(PN＋1)2的数必是素数，且其个数是可统计确定的.

已知方程a2＋b2－P（1＋ab）＝ 0，当a，b，P为正整数时，求a，b，P的解集.

说明：在方程a2＋b2－P（1＋ab）＝ 0 中，若其解（a，b，P）为整数，则称（a，b，P）为方程a2＋b2－P（1＋ab）＝ 0 的解形式.当（a，b，P）为正整数时，也称（a，b，P）为方程a2＋b2－P（1＋ab）的解形式，或方程的正解形式.所以，上述之意也是在求方程a2＋b2－P（1＋ab）＝ 0 的正解形式.

解：设方程a2＋b2－P（1＋ab）＝ 0 的解形式为｛a，J（［a，m］，［a，n］）｝（J为正整数）.（为什么会这样去假设，只是在解二元一次方程的解形式与三元一次方程的解形式中有所感悟而为之）.

所以原方程变为：a2＋（aJ＋m）2－（aJ＋n）［1＋a（aJ＋m）］＝0，

推出a2＋a2J2＋2maJ＋m2－（aJ＋n）（1＋a2J＋am）＝ 0，

推出a2＋a2J2＋2maJ＋m2－［（aJ＋a3J2＋a2Jm）＋n＋na2J＋nam］＝0，

推出a2＋a2J2＋2maJ＋m2－aJ－a3J2－a2Jm－n－na2J－nam＝0，

整理，得－a3J2＋a2（1＋J2－Jm－nJ）－a（nm－2mJ＋J）＋m2－n＝0，

由于－a3J2是独立项，故J2＝0，得J＝0.

当J＝0 时，则a2－anm＋m2－n＝0，

所以，a（a－nm）＝ 0，m2－n＝0，得a＝m3，n＝m2，

所以，方程a2＋b2－P（1＋ab）＝ 0 的解形式为（a，b，P）＝｛m3，0（［a，m］，［a，m2］）｝.

由于a2与b2项系数相同，故（a，b，P）＝ （b，a，P）＝ ｛m3，m，m2｝ ＝｛m，m3，m2｝.

由于a2与b2是二次函数，所以，当a＝m3，P＝m2时（当a＝m，P＝m2时，b＝m3（m为正整数）），

则方程a2＋b2－P（1＋ab）＝ 0 变为（m3）2＋b2－m2（1 ＋m3b）＝ 0，

推出m6＋b2－m2－m5b＝0，

推出b2－m5b＋m6－m2＝0，

因式分解，得（b－m）［b－（m5－m）］＝ 0，得b＝m，或b＝m5－m＝m（m4－1）.

当b＝m时，已有正解形式，当b＝m（m4－1）时，方程的解形式为（a，b，P）＝ （b，a，P）＝ ｛m3，m（m4－1），m2｝ ＝ ｛m（m4－1），m3，m2｝.

由于a，b，P为正整数，故在正解形式｛m3，m，m2｝中，m为大于0 的正整数.

在正解形式｛m3，m（m4－1），m2｝中，m为大于 1 的正整数.

综上，正解形式中，P＝m2始终成立，即P总是某正数的平方.

如果没要求a，b，P是正整数的话，那么，以上两个正解形式也是其解形式，却不完全，在此就不多做说明.