关于高中数学离心率题型解法的有效解决技巧

杨新波

【摘要】在高中数学中，离心率是一个比较抽象的概念，它是描述圆锥曲线性质的一个的概念，同时它也是圆锥曲线的一个非常重要的属性。离心率的定义是：到定点的距离与到直线的距离的比是常数（记作）的点的轨迹叫做圆锥曲线，其中常数就是圆锥曲线的离心率，它可以描述椭圆的扁圆程度、双曲线的开口大小，所以这类知识相关的题型所考察的重点是离心率的数值。但是由于离心率的概念比较抽象，给学生的学习增加了一定的困难。本文就关于高中数学离心率题型解法的有效解决技巧进行研究。

【关键词】高中数学;离心率;题型解法

引言

数学解题思想的关键之处在于把学生所学的知识融合在一起，有利于巩固学生所学的数学知识点，这帮助学生建立一个良好的认知结构，发展学生的逻辑推理能力，提高高中数学的教学质量和教学水平。每一类数学题型都有相应的解题技巧，只要学生掌握了该类题型的解题技巧，就能够达到举一反三的教学效果。

一、高中数学离心率题型的概念

在高中数学教材里，离心率是一个比较重要的几何概念，因此离心率与几何图形有着非常紧密的联系，圆锥曲线的离心率题型是高考中重点题型，一般都以压轴题的形式出现，而且离心率题型考核的形式多种多样，考试题型将斜率、平行、离心率以及向量结合在一起，甚至与物理知识相结合。高中数学的离心率题型主要考察学生的数学综合能力，因此高中数学教师在教学的过程中，教师要引导学生对离心率题干中信息进行分析，寻找出已知信息，找到解题思路，进而达到解题的目的。

二、高中数学离心率题型的解题技巧

在笔者的教学过程中对学生进行离心率知识点教导时，引导学生培养从简单的变数中观察隐含的数学规律，培养学生善于用数字、图形相结合的思想解答高中数学的几何题。初次之外，高中数学离心率对高中生的数学计算能力、设想能力有充分的考验，部分学生因为对高中数学的离心率比较畏惧，所以在考场上一旦有离心率的题型就选择“不答”的情况，针对这种情况，高中数学老师一定要注重突破学生的畏惧心理，在教学中结合经典例题帮助学生找到高中离心率题型的突破口

1、认真审题，捕捉“题眼”

审题是高中数学离心率题型解答的首要步骤，有助于学生从离心率的知识点正确的解答思路进行切入，挖掘隐藏条件，避免解体出现失误。所以在日常练习过程中应该注重审题，避免出现因题目的相似性而匆匆答题导致失分。以

例题1：考察双曲线的标准方程及公式的题目为例：若双曲线的离心率是2，则实数的值是多少？

从这道例题来看根据双曲线的标准方程式确定、，根据公式求出的值，得出.

2、明确考点，正确计算

高中数学解答题能够考查学生对知识点的把握和计算能力，是一种综合性考查方式。所以高中数学解答题不仅要求学生会解答，更要注重答题的高效性，达到在有限的时间中凭借自身所掌握的知识点取得更多的分。所以高中数学的离心率学习过程中注重培养学生的等价转化思想、函数方程思想、分类讨论思想。在答题过程中结合综合思想把握考点，进行正确的计算。

例题2：已知、是椭圆C：（a>b>0）的左、右两个焦点，若椭圆C上存在一点M，使得，求椭圆离心率的取值范围。

这道题需要学生根据椭圆的定义和条件建立方程，利用基本不等式建立、的不等式，从而求出椭圆离心率的取值范围进而进行解答。

3、语言规范，书写工整

高中数学离心率解答题是高中数学考试的必考重点之一，并且解答过程中要求学生数学较为繁琐的解题过程。若在解答过程中出现语言不规范、字迹不整齐的情况则会导致阅卷老师阅读不清，导致考试丢分。所以高中数学老师在日常教学过程中，教师应该做好引导，保证学生在离心率解答题的解答过程中用语规范，字迹工整。

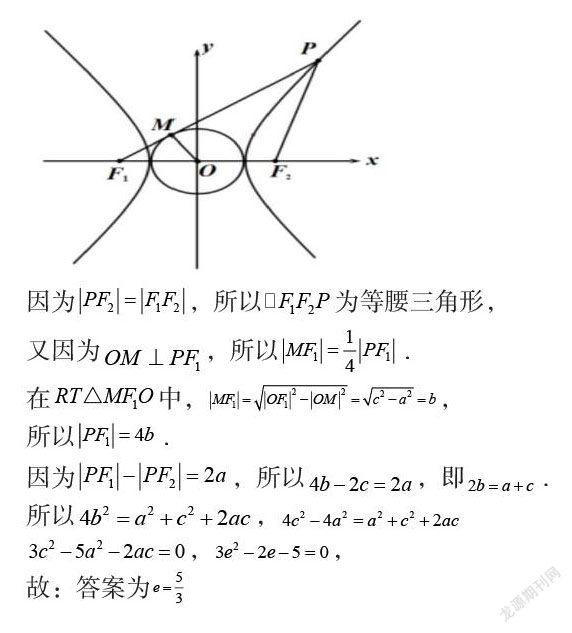
例题3：双曲线的左右焦点为，是双曲线上一点，满足，直线与圆相切，求双曲线的离心率.

本道例题主要考察学生的思维能力以及对几何的解析能力，求解双曲线的离心率或离心率的取值范围，是高中数学离心率考察的重要题型，也是近年来高考的热门题型之一，同时也是高考数学的重点内容，解决该类问题的关键之处在于把握曲线的本质，根据已经信息，理清曲线与圆的位置关系，进而达到求解的目的。

结束语：综上所述，离心率是近年来数学高考的重要题型也是常考题型，高中数学老师在开展教学过程中从解题思路进行教学之外注重从多个层面考查学生对圆锥曲线知识和分析问题的综合能力。离心率作为圆锥曲线中的重要元素之一，其变化会直接影响着圆锥曲线的形状和类型，所以轨迹问题与圆锥曲线的三要素密切相关。除此之外由于不同的圆锥曲线的离心率有着不同的范围，所以在解答过程中求取参数的取值范围是近年来的重点考题之一。除了以上答题技巧之外，高中数学老师对学生的答题规范和答题重点应该做到时刻关注，避免学生出现失分的情况。

参考文献：

[1]王晓云.高中数学求离心率e值的解法初探[J].教书育人，2017（20）：79-79.

[2]沈文慧.高中数学“离心率问题”的求解方法[J].理科考试研究：高中版，2015，22（11）：6-6.

[3]孟凡勋.圆锥曲线离心率问题的探究策略[J].高中数學教与学，2018（2）：123-124.