直观图一例的辨析与思考

摘 要：在直观图一节的教学中有很多问题容易引起师生的争论，且无法以课本内容分析出确定的结论。下面以一例说明直观图中一些问题及笔者的分析，期待抛砖引玉，得到更多老师及同学对此问题的探索和高见。

关键词：直观图;辨析;思考

引言：有一个角为60°的直角三角形，其直观图可否为等边三角形？

教辅书上的答案是否定的，事实上，在很多教师和学生的认识中，直观图的画法应该只有或者默认只有斜二测画法。对于这个问题，首先，直观图显然不能只有斜二测画法这一种画法，甚至未必是空间几何体经过平行投影得到的图形，教材上介绍的是“直观图是表示空间几何体的平面图形”。我们应该注意到，涉及到斜二测画法的题目，会提到“由斜二测画法得出的直观图”，若是默认，显然无需此说。

基于以上分析，问题中的直观图我们未必要用斜二测画法得出，那么，此题的结论究竟是否正确，若题中明确要求必须由斜二测画法得出直观图，此题结论又是否正确？该如何分析？

一、有一个角为60°的直角三角形，其直观图可否为等边三角形？

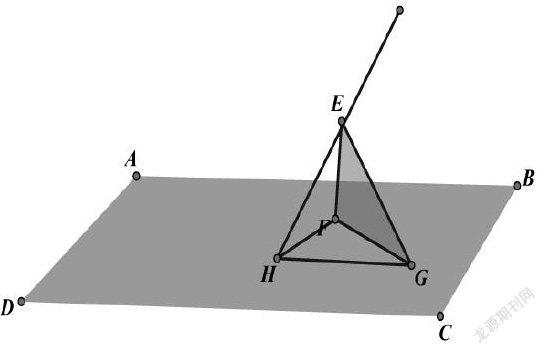
如图，可以通过构造，我们将一个角为60°的直角三角形EFG的60°角FEG所对的边FG放在投影面ABCD上，且令面EFG与面ABCD垂直。投影線EH与投影面ABCD所成角为30°，这样，保证了EF的影子HF长度与三角形的边FG相同，此时，只需同时保证投影线EH与面EFG所成角余弦值为（事实上，是为了保证三角形HFG三边相等），即可使得三角形EFG在投影面ABCD上的投影为等边三角形。

二、一般的直角三角形直观图可否为等边三角形？

这个构造的方式与问题一中方式相同，可以构造出合适的投影线和投影面，使得一般的直角三角形直观图为等边三角形。事实上，一般的三角形都可以通过构造使得其直观图为等边三角形，构造方式并不困难。这里，就不构造证明了。

即我们通过对此例的探讨，得出以下结论：任意三角形的直观图都可能为等边三角形。

三、有一个角为60°的直角三角形，其由斜二测画法得出的直观图可否为等边三角形？

定理1：斜率为k的直线，在斜二测画法得出的直观图中中直线的斜率为（将仿射坐标系中的点也看做平面直角坐标系xOy中的点）

利用这个引理，我们不妨设平面直角坐标系中两直线斜率分别为k1，k2，①，若k1，k2还可以同时满足②，则在平面直角坐标系中60°的角，在由斜二测画法得出的直观图中是可能大小不变的。

联立①②，可得③

不妨先假设k1，k2为方程的两根，再证明方程确实有两不同根即可。

由③可得，④

由①可得，

得到，

即，即⑤。

联立④⑤可得该方程判别式，且两根，不妨令则，使得b有解。且此时方程的判别式。

四、总结

综上，有合适的k1，k2同时满足①②，我们发现只要三角形在坐标系中放置的“方向”合适，完全可以使得60°角不发生变化，所以，这个观点并不能解决第三个问题。

因此笔者采取如下方式解决：

定理2：xOy平面内的点（x，y）变换到平面内的坐标变为（将仿射坐标系中的点也看做平面直角坐标系xOy中的点）

建立坐标系，令，则为满足条件的三角形。则变换后对应点坐标分别为若形成等边三角形，则有，通过运算容易发现并无合适的α满足上述条件，所以有一个角为60°的直角三角形，其由斜二测画法得出的直观图不可能为等边三角形。至此，问题三得到了解决。

参考文献

[1]由斜二测画法得到的直观图若干性质，上海中等数学.2009（9），39-40.

作者简介：王爽（1983.7.21）女，汉族，哈尔滨德强学校高中部，中教一级，理学硕士，研究方向：应用数学