探究解析几何学习障碍及教学对策

刘保灼

摘 要：数学是高中阶段的主要教学科目之一，在数学教学的过程中，解析几何是一个重要的知识内容，在高考当中也有着很大的占比，并且和其他的数学知识内容之间也有着很深的关联，可以说解析几何是能否学好高中数学知识的关键。但是数学知识具有一定的抽象性特征，尤其是在解析几何当中更是得到了全面的体现，所以高中生学习起来就会有一定的障碍，需要我们找出合理的教学对策。本文对高中数学解析几何的教学对策进行探究，期望能够提供一些有效的帮助。

关键词：高中数学教学;解析几何;障碍;对策

一、解析几何学习障碍

（一）知识理解障碍

解析几何作为高中数学阶段的主要知识内容，也有着具体的细分，双曲线、抛物线以及椭圆是我们在学习解析几何知识过程中的主要内容，学生在学习相应知识的过程中，往往会有一定的理解障碍，不仅无法掌握解析几何的具体应用方式，甚至于对解析几何的基础理论也不是很明确。除此之外，高中生也没有过多的解析几何学习时间。高中数学教师在教学中，只能够将教材上的内容进行灌输式教学，无法保障学生理解具体的内容及有效的应用。多种原因导致高中生在学习解析几何时面临着理解的障碍。

（二）实际应用障碍

在进行解析几何知识的实际应用过程中，高中生也会面临着一定的障碍。在运算的过程中，会接触到很多复杂的计算，往往一个微小的失误就会导致全盘皆输，如若学生的数学运算能力不强，那么在进行解析几何相关问题的解答过程中，也就会面临着很大的阻碍。

（三）数形转化障碍

解析几何是图像和解析式之间相互结合的形式，在进行解析几何的学习和应用过程中，就一定要学会进行数形转化。在实际的学习和问题解答过程中，仍然有相当部分学生没有掌握数形转化的方法和思想，往往只将解析式和函数图像看做两个单独的主体，没有办法进行结合分析，所以对知识的掌握不够深入，解答相关的问题也不够高效。除此之外，平行向量也是我们应当掌握的一种方法和思想，能够将函数图像和代数之间进行相互转化，帮助我们更加简便的解答相应知识内容，但是往往高中生并没有真正的掌握平行向量的应用方式，对解析几何的理解程度也就不深。

二、解析几何教学对策

（一）幫助学生打好基础

针对解析几何当中的主要教学内容，我们也应当掌握好具体的教学手段。双曲线、抛物线以及椭圆，虽然相互之间具有一定的差别，但是还是拥有着较为明显的共性，我们应当帮助学生通过一个概念来理解和分析另外两个知识内容，让学生更全面的认识和理解解析几何相关知识。我们可以将一个圆锥进行分割，观察圆锥的横截面，让学生来理解相应的知识内容，帮助学生将这三个重要的知识部分联系起来，并且掌握好基础的知识内容。通过相应的教学方法，能够帮助学生打好基础，帮助学生更好的理解和掌握解析几何相关知识，并且提升学生解答相关问题的效率。

例如：已知椭圆x2/（7-a）+y2/（a-2）=1的焦距为5，求a的值

分析：本题考查椭圆的性质，考查学生对椭圆方程的理解，属于基础题，分焦点在x，y轴上讨论，结合焦距为5，可求a的值.

但有部分学生因对椭圆的知识理解不深入导致解题只考虑一种情况而出错。

解答：由题意，焦点在x轴上，7-a-a+2=5，所以a=2;焦点在y轴上，a-2-7+a=5，所以a=7，综上，a=2或7.

故答案为：a=2或7.

（二）提升实际运算能力

运算能力是决定着解析几何问题解答效率的主要因素，我们在平时的教学过程中，应当注重培育学生的运算能力，避免在考试的过程中出现不必要的差错。我们可以将具体的解析几何相关问题进行剖析，带领学生分析问题当中给出的条件，然后利用这些条件进行逐步分析，让学生明白合理的解析结合问题解答步骤。除此之外，相应的练习也是必不可少的，我们可以给学生布置一些解析几何相关的训练问题，让学生进行相应的解答，例如“已知抛物线P：x2=2py （p>0），求抛物线P的方程。”在解答这个问题的过程中，学生就需要进行大量的计算，计算出准线距离，并且最终得出X2=4Y的结果，通过不断的类似练习，来逐渐提升运算能力，并且缩短运算的时间。运算能力的提升能够帮助学生更高效的解答解析几何相关问题，并且在考试的过程中合理安排时间，获得满意的分数。

（三）培育数形结合思想

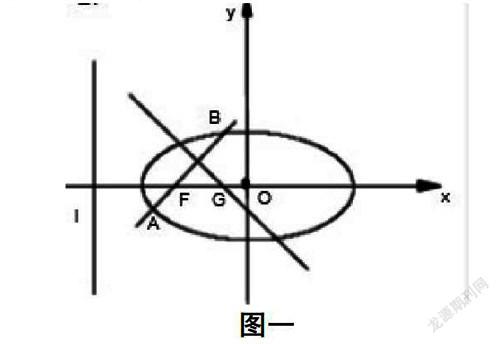
数形结合思想是理解解析几何相关知识，解答解析几何问题的关键，这需要我们在解题的过程中利用好相关的工具。平面向量以及平面坐标系是我们应当注重的解题工具，能够将函数图形和具体的解析式之间构建明确的联系，学生在解答相关问题的过程中，就可以快速的进行数形转换，可以将一些我们隐含的条件找出，在解答解析几何问题的过程中也能够做到更加的高效。例如在进行：“椭圆X2/2+Y2=1的左焦点为F，O为坐标原点，求过点O、F，并且和左准线L相切的方程”这道问题的解答过程中，我们就可以利用平面坐标系进行辅助（图一），最终得出（X+1/2）2+（Y±√2）2=4/9。所以，培育数形结合思想是我们在教学过程中需要注重的内容，通过平面向量以及平面坐标性的辅助，构建数与形之间的转化渠道，帮助学生解答解析几何相关问题，提升我们的教学效率和质量。

结语：解析几何是高中数学教学过程中的主要内容，由于数学具有一定的抽象性特征，所以高中生在进行解析几何学习的过程中就会面临一定的障碍，需要我们掌握合适的教学对策，来帮助高中生掌握解析结合知识，高效解答解析几何问题。要注重基础理论的教学，帮助高中生打好基础，提升运算能力，提升计算的精准性，以及注重培育数形结合的思想，利用平面向量以及平面坐标系，进行数形转化。通过种种教学对策，帮助高中生更好的掌握解析几何知识。

参考文献

[1]郭永卫.高中解析几何学习难点及教学对策[J].课程教育研究，2015，36：195-196.

[2]戴加艳.解析几何学习障碍分析及教学对策[J].数学学习与研究，2017，05：43.

[3]张青豫.《立体几何》学习障碍及教学对策浅析[J].青海教育，1998，Z1：72.