高中数学解题中等价转化思想的应用研究
江海波

摘 要:解答高中数学习题时,引导学生运用一些解题思想,可使其少走弯路,快速得出正确结果,促进学生解题能力的提升.其中等价转化思想在解答数学习题中较为常用.为提高学生应用该思想的意识与能力,授课中既要注重讲解该思想的一些理论知识,又要讲解相关例题,给其更好的应用于解题中提供参考.
关键词:高中数学;等价转化思想;应用;研究
等价转化思想是指运用所学知识将原来难度大,不易解答的问题转化为难度小,方便解答问题的一种思想.高中数学解题中应用的等价转化思想分类较多,主要包括等体积转化、正与反的转化、方程根与图象交点的转化等.为保证解题的正确性,转化后不能改变问题的本质.
一、等体积转化的应用
等体积转化在高中数学立体几何习题中较为常用.该类转化思想的应用难度并不大,应用时应把握“等体积”这一关键.授课中为提高学生应用该等价转化思想解题的意识,应为学生总结该思想能够解答的问题,包括几何体的体积、点到面的距離、几何体某一面的面积等.另外,在课堂上讲解相关例题,使学生体会转化的具体过程,更好地消化、吸收这一重要的转化思想.同时,思考该思想适用的题型,遇到类似题型,及时找到解题思路,少走解题弯路.
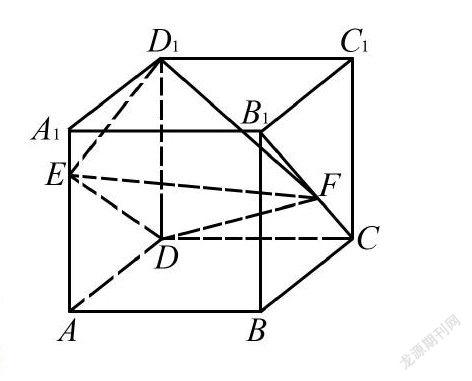
例1 如图1,在棱长为1的正方体
ABCD-A1B1C1D1中,AA1和B1C上分别存在E、F两点,则三棱锥D1-EDF的体积为().
A.1B.12
C.14D.16
该题难度并不大,关键在于找到正确的解题思路.因E、F两点在AA1和B1C上的具体位置未知,因此,采用直接法难于求解.此时可考虑等体积转化法求解,即借助VD1-EDF=VF-EDD1进行解答.
由图不难得出S△EDD1=12×D1D×AD=12.而点F到面EDD1的距离为AB=1,则VF-EDD1=13×S△EDD1×AB=13×12×1=16.D为正确选项.
应用等体积转化思想解答数学习题时应具备灵活的头脑,既要能够从整体上把握题干,又要充分挖掘隐含条件,做好巧妙的转化,降低解题难度.正如上题之所以将三棱锥置于正方体之中,实则间接地告知学生点F和底面EDD1的距离为1.
二、正与反转化的应用
正与反的转化属于等价转化的一种,在高中数学解题中应用范围较广,既可用于解答集合习题,又可用于解答函数、概率等问题.为使学生感受到正与反转化在解题中的简便之处,应结合学生所学做好相关例题的讲解,给其以后应用于解题中带来良好启发.同时,鼓励学生多做训练,能够根据问题的正面,准确地找到其反面,如此才能保证转化后解题结果的正确性.
例2 已知m∈R,已知命题P:|m-5|≤3.命题Q:函数f(x)=3x2+2mx+m+43有两个不同的零点,求使命题“P或Q”为真命题的实数m的取值范围.
命题“P或Q”为真命题存在三种情况,讨论起来较为麻烦,容易出错,因此可将其转化成命题的反面,得出结果取反,则能在保证结果正确的基础上大大提高解题效率.
针对命题P不难求出m的取值范围为:2≤m≤8.命题Q中要想满足函数f(x)=3x2+2mx+m+43有两个不同的零点,则应满足Δ=4m2-4×3×(m+43)>0,得到m>4或m<-1.当两个命题均为假,则满足m<2或m>8,-1≤m≤4,得到-1≤m<2,则满足题意的m的取值范围应为(-∞,-1)∪[2,+∞).
运用正与反转化解答有关命题的习题时应具体情况具体分析,思考从正面解答是否进行分类讨论.如需要考虑的情况较多则应进行转化,从反面入手解答即可,应用中不可思维定势,生搬硬套.
三、方程根与图象交点转化的应用
方程的根与函数图象交点关系密切,将两者进行转化在解题中较为常见.为使学生掌握相关的转化思路,灵活应用于解题中,授课中讲解转化的注意事项,对方程进行适当的移项,找到两个函数.同时,绘制函数图象前应充分挖掘题设隐含条件,找到准确的定义域范围,保证函数图象绘制的正确性.另外,结合具体的问题情境,为学生讲解方程根与函数图象转化的具体应用,使其通过听讲,准确把握转化的一些细节.
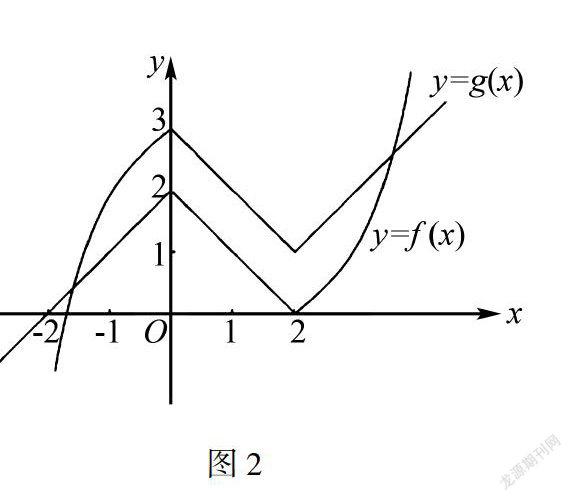
根据经验求解方程根的个数通常转化为两个函数的图象交点问题.题目中f(x)为分段函数,而g(x)函数并未直接给出,因此,解题的关键在于确定函数g(x)表达式以及绘制函数图象上.
图2根据函数f(x)的表达式求出函数g(x)的表达式.当2-x≤2,即当x≥0时,g(x)=3-(2-|2-x|)=|x-2|+1.当2-x>2,即x<0时,g(x)=3-(2-x-2)2=-x2+3.在同一平面直角坐标系中绘制出两个函数的图象,如图2所示,两个函数图象的交点为两个,对应f(x)-g(x)=0根的个数为2个.
运用方程根与函数图象交点转化思想解题时,先不要急于动笔,应认真观察,将原方程拆分成熟悉的函数,或确定未知函数的表达式,而后根据所学绘制函数图象,找到函数交点问题也就迎刃而解.
等价转化思想是解决数学问题的重要思想之一.为使学生牢固掌握该思想,灵活用于解题中,授课中应做好常用等价转化思想的汇总与相关知识的讲解,并结合例题讲解其具体应用,给学生更好的应用于解题中带来良好的示范,使其把握该思想在解题中的应用关键.
参考文献:
[1]吕丽.等价转化思想在高中数学解题中的应用[J].中国校外教育,2019(29):79-80.
[2]薛豪.等价转化思想在高中数学解题中的应用[J].科学大众(科学教育),2019(03):19.
[3]杨新运.等价转化思想在高中数学解题中的应用[J].福建基础教育研究,2017(10):61-62,65.
[责任编辑:李 璟]

