拨开云雾，探究本源，打造高效课堂

高海强

摘要：在数学教学中应合理、科学地设置情景，让学生探索结论，并对此进行证明。从而让学生弄清问题的“来龙去脉”，甚至由此发现巧妙的解法，以及有趣的结论，达到举一反三的效果，同时以培养学生能提出数学问题，解决数学问题的能力。

关键词：本源;平行线;来龙去脉;数学

对待数学教学中所设置的情景，不仅要探索解决它的途径，给出它的严格证明，而且还应该继续深入思考，并作多方面的探索。例如，同样条件寻求可能出现的多种结论，以广开思路，增强分析和解决问题的能力;溯源探幽，以弄清问题产生的“来龙”;推广题意，以看出问题发展的“去脉”;因为弄清问题的“来龙去脉”，正是理解深入的标志之一。进而适当变换题目的形式和条件，为灵活运用奠定基础，再广泛联想，从横向对比中挖掘出联系，真正的究其本源，达到高效。

1 设置情景，广开思路，培养发散思维

对于同一个问题，改变题目中某些条件，结论有什么变化呢？这样既能广开思路，以收到培養发散思路之效，又能帮助学生加深对问题的认识。因为同一情景素材，条件略有改动，结论又有什么变化规律呢？往往是从各自的侧面，相异的渠道反映出，条件与结论之间的联系。对此，不妨看如下情景材料：

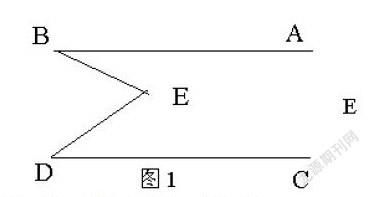
例1、如图：已知，AB∥CD，求证： （猜想结论，并给予证明.）

（1）假设E是一动点，作如图2运动

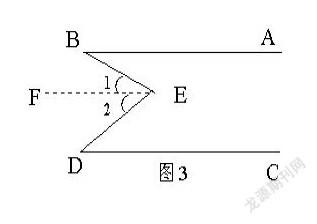
当E点在平行线AB与CD之间时，如图3，则：∠B+∠D=∠BED。

证明：过点E作EF∥AB，则有EF∥CD.

∵EF∥AB（作图）

∴∠B =∠1（两直线平行，内错角相等.）

∵AB∥CD，EF∥AB

∴EF∥CD（平行公理的推论）

∴∠D =∠2（两直线平行，内错角相等.）

∴∠BED =∠1+∠2 =∠B+∠D

即：∠B+∠D =∠BED

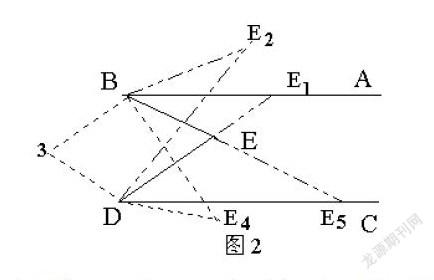
（2）当点E在E 1或E5时，如图4，结论相似，即：∠1 =∠D，∠2 =∠B .

证明：∵AB∥CD （已知）

∴∠1 =∠D，∠2 =∠B （两直线平行，内错角相等.）

（3）当点E运动到E2或E4的位置时，如图5，结论相似，即：

∠2 =∠3+∠4，∠7 =∠5+∠6.

证明：∵AB∥CD （已知）

∴∠1 =∠2（两直线平行，内错角相等。）

∵ ∠1=∠3+∠4（三角的任意一个外角等于与它不相邻的两个内角之和）

∴∠2=∠3+∠4

同理：∠7=∠5+∠6

（4）当点E运动到E3时，如图6，则：∠B+∠E+∠D=3600

证明：过E3作E3F∥AB，由平行公理的推论可得，E3F∥CD 。

∵E3F∥AB，

E3F∥CD，

∴∠1+∠B=1800，

∠2+∠D=1800（两直线平行，同旁内角互补。）

∴∠B+∠1+∠2+∠D=3600

即：∠B+∠E+∠D=3600

（5）当∠BED=900，BF是∠ABE的平分线，DF是∠CDE的平分线，如图7，则：∠F=  1/2∠BED=450

证明：过F作FG∥AB，由平行公理的推论可得，FG∥CD 。

∴∠1 =∠2，∠3 =∠4，（两直线平行，内错角相等。）

∴∠BFD =∠2+∠3 =∠1+∠4，

又由（1）∠BED =∠ABE+∠CDE，

∵∠BED =900，∴∠ABE+∠CDE=900 （等量代换）。

∵∠1= 1/2∠ABE，∠4= 1/2∠CDE（角平分线的定义），

∴∠1+∠4 = 1/2 ∠ABE+ 1/2  ∠CDE

=  1/2 （∠ABE+∠CDE）=450

即：∠BFD =1/2  ∠BED=450

2 溯源探幽，弄清问题的“来龙”;变形推广，看出问题的“去脉”

对于“一元二次方程根的判别式”来说，教师在讲完新知以后，可以安排学生进行“实战演习”，即用根的判别式去判别方程的情况.为了进一步加深学生的理解运用，教师除了要让学生判别“”这样的完整的实数方程以外，也要让学生尝试去判别一些带字母的方程式，如“”，这样的式子需要学生进一步开动脑筋，运用自己的理性思维去判别m不同取值范围下方程根的分布情况.总之，习题的设置既要帮助学生对所学内容进行巩固，还须有一定的延伸拓展，能发展学生的抽象思维.

总之，我们在数学教学中应合理、科学地设置情景，让学生探索结论，并对此进行证明。从而让学生弄清问题的“来龙去脉”，甚至由此发现巧妙的解法，以及有趣的结论，达到举一反三的效果，同时以培养学生能提出数学问题，解决数学问题的能力。

（作者单位：重庆市云阳县红狮初级中学）