提升中职三角函数教学效果的有效策略

谢加丽

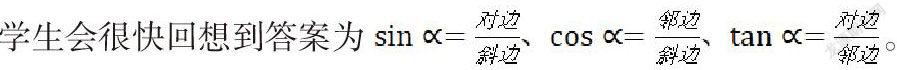
摘要：在中職数学教学中，由于知识、学生、教师与环境等方面都对其教学具有影响，造成课程知识讲解的困难。通过调研发现，三角函数知识是教学过程中所存在的难点，所以本文将针对于三角函数这一内容出发，分析其中影响教学的因素，探究提升教学效果的有效策略。

关键词：中职数学;三角函数;策略

引言：

三角函数是中职数学学习的重点内容，但是在讲解过程中都很难取得优秀的效果，其中主要所依存因素出自于学生、教师与环境三方面。所以针对于这三方面，提出了解学生基础与转化思维这两点建议与策略。

一、影响中职三角函数教学效果的因素

（一）教师因素

教师作为教学中的引导者与课堂的建设者，在对于这一课程教学中，必须对于所教学的三角函数内容具有较为深刻的理解。在教学中，教师可通过构建一个三角函数的知识框架，从而引导其进行知识的学习。教师主要结合对其理解，从其知识基础上进行知识的添加，使其构建出三角函数的知识框架。教师必须做好引导作用，调动起学生学习的自主性，调动起学习自主性的方法^[1]。

例如，通过教师对内容的理解，从而设计不同的问题，运用问题串的方式，由简到难，慢慢调动学生积极性，之后慢慢进行知识的讲解，呈现阶梯型学习，最后成功在其知识结构中构建三角函数知识的知识框架。

（二）学生因素

由于中职院校在招生过程中，所报考的学生都具有不愿意进行主动学习、学习基础差与学习能力差的特点。所以在进行中职数学学习过程中，是很难理解知识与习题的，主要是由于缺乏数学学习思维与能力。第一，在进行三角函数知识学习中，所缺失的思维能力最为主要是抽象思维，所以难以理解其中的知识或者习题信息，在进行解题过程中对于习题难以解读，从而降低了解题的质量。第二，同时由于学生在学习过程中缺乏自主性以及目的性，所以在进行学习过程中，主要是为应付考试，并不是为了之后的专业知识学习与未来的就业进行考虑。第三，同时由于学生在学习过程中具有懒惰性，也缺乏自信心，在学习过程中主要是进行糊弄，或者直接选择放弃学习。第四，学生在学习过程中，并未养成学习的兴趣，从而在进行知识学习过程中，对于所学习的内容并不关注，在加上教师的不注重，造成对学习的方式，即使学习也会采用死记硬背的方式进行记忆。结合以上四点，很难取得优秀的三角函数学习效果。

（三）教学环境因素

良好的教学环境是中职数学的重要依存环境。但是由于在社会中对于中职学校的认可度不高，并且其中的资金投入也较低，所以在课程设计中也并不完善，学习不具有高效性。这一大学习环境造成了学生对数学学习的厌恶，在三角函数学习中也不具有学习的动力。并且在现阶段信息化时代中，各种设备的出现，如手机、电脑等设施，逐渐分散了学生的注意力，更是使其沉迷于网络中，造成学习效率的更低下。

所以针对于以上的原因，教学环境的创设已经不仅仅是教师与学习的任务，更主要是整个社会的任务。只有扭转人们心中中职的地位，才能引导学生走出对中职误区，抓住学习的机会进行知识的学习，并自主锻炼自身，奠定良好的基础。

二、提高中职三角函数数学效果的有效策略

（一）全面了解中职生三角函数知识基础

教师在设计教学过程中，必须注重学生在课堂中的主体地位，对其知识结构具有一定的了解，从而抓住其中的重难点，顺应其学习的规律，培养其学习的兴趣，从而参与到数学知识的学习。教师也可通过对学生的了解，从其实际发展状况出发，以其能力与智力出发，深入挖掘三角函数知识，进行针对性的课程设计，确保知识与学生之间的高度吻合，从而提高中职数学知识教学的效果，并且在针对性的学习中，更容易掌握其中的方法与思想，构建出其中的三角函数知识结构。并且针对于学生不愿意自主学习、缺乏兴趣的状态，就需要教师创新教学方式，选择一个优秀且适合于同学们的方式，将方法与知识相融合，从而在获取知识的过程中，得到能力与思维的提升，以及知识的运用能力。在教学过程中所使用最为有效且广泛的方式，就是抓住知识与实际生活之间的联系，进行知识的构建^[2]。

例如，在学习三角函数中“关于终边相同的角”这一知识时，教师可选择生活中摩天轮这一实际案例，讲述：大家思考所看过的摩天轮，假设以最高点为起点，在旋转一周时，其多少度？旋转到最低点时，是多少度？如果以从最低点出发，在旋转一周是多少？从生活中案例出发，轻松讲解了“任何一个与角终边相同的角，都可以表示成角与整数个周角的和”。

（二）转换中职生三角函数数学思维

思维能力是十分重要的内容，是对学生知识与能力进行转化的重要基础。三角函数知识的学习在初中时期已经简单涉及，但当时所学习的内容较为简单，并且知识较为具体化与形象化。所以为更高的讲解这一内容，就需要转化这一学习内容，将其形象化转化为抽象性，但是这一过程中，就需要学生具有较强的抽象思维能力与逻辑思维能力，才能完成这一知识的学习。在完成这一知识的学习后，可以成功拓宽学生学习的思路，锻炼其思维能力，在脑海中形成更完善的知识结构。并且在习题解答过程中，也会轻松发现其中所包含的各种性质与定义，从而找寻其中的解题方式与解题方法，提高解题教学的质量。在教学过程中，教师可通过提问与数形结合的方式，进行思维的转化，一步步引导学生进行知识的回忆与知识的重构，从而在脑海中，形成一个更加完善的知识体系，并实现思维的锻炼^[3]。

例如，在讲解三角函数的定义这一知识时，

教师可以提出第一个问题：回忆在初中时期所学习的锐角三角函数知识？其中sinα、cosα、tanα这三个函数值都是怎样进行表示？

学生会很快回想到答案为。

在回答完问题后，教师及时提出第二个问题：大家思考一下，这一公式运用中所包含的自变量取值范围、函数值取值范围以及各种使用条件什么？

学生可以通过回忆之后很快就解决其中的问题，并且对于这一知识学习的信心也不断增加。

教师顺势提出第三个问题：在高中数学的学习中，这一知识不能在只限制于锐角三角形中，那么大家思考一下，如何将这一函数运用在钝角三角形中？

学生在看到这一问题时，受到以上两个问题的自信心，会勇于进行试验的探究。但是这一过程中需要注意，学生缺乏这一抽象思考能力，很容易会受到这一问题影响自信心，所以教师必须迅速做出提醒，防止其松懈信心，指出可以将三角形放在直角坐标系中。之后学生进行探究，就开始找寻其中的特点，教师可选择适当再进行提醒解决问题或者在其发现某一特点后进行问题讲解。保证其参与度，助长其自信心，从而进行之后更深入学习。

方法：“坐标法”使用坐标进行三角函数的探究，其中斜边变为一个于原点为出发点的线段，长度为1，保证其计算简便。从而将边长问题，转化为坐标问题。

结束语

在中职数学学习中对于三角函数的学习，一直是较为困难的学习内容，其中主要是教师、学生与学习环境的影响，造成学习效率的降低。所以从两方面出发，分别为中职生的基础知识与数学思维，找寻更好的教学策略，实现课堂的高效。

参考文献

[1]白立庆.中职数学三角函数内容的改进[J].中国校外教育，2019（35）：160-161.

[2]蒋永桃.关于中职数学三角函数最值教学方法的探讨[J].科教文汇（下旬刊），2019（10）：136-137.

[3]刘子礼.中职数学三角函数最值教学思路探析[J].课程教育研究，2019（08）：148-149.