解密一次函数图象分布
崔秀玲 左效平
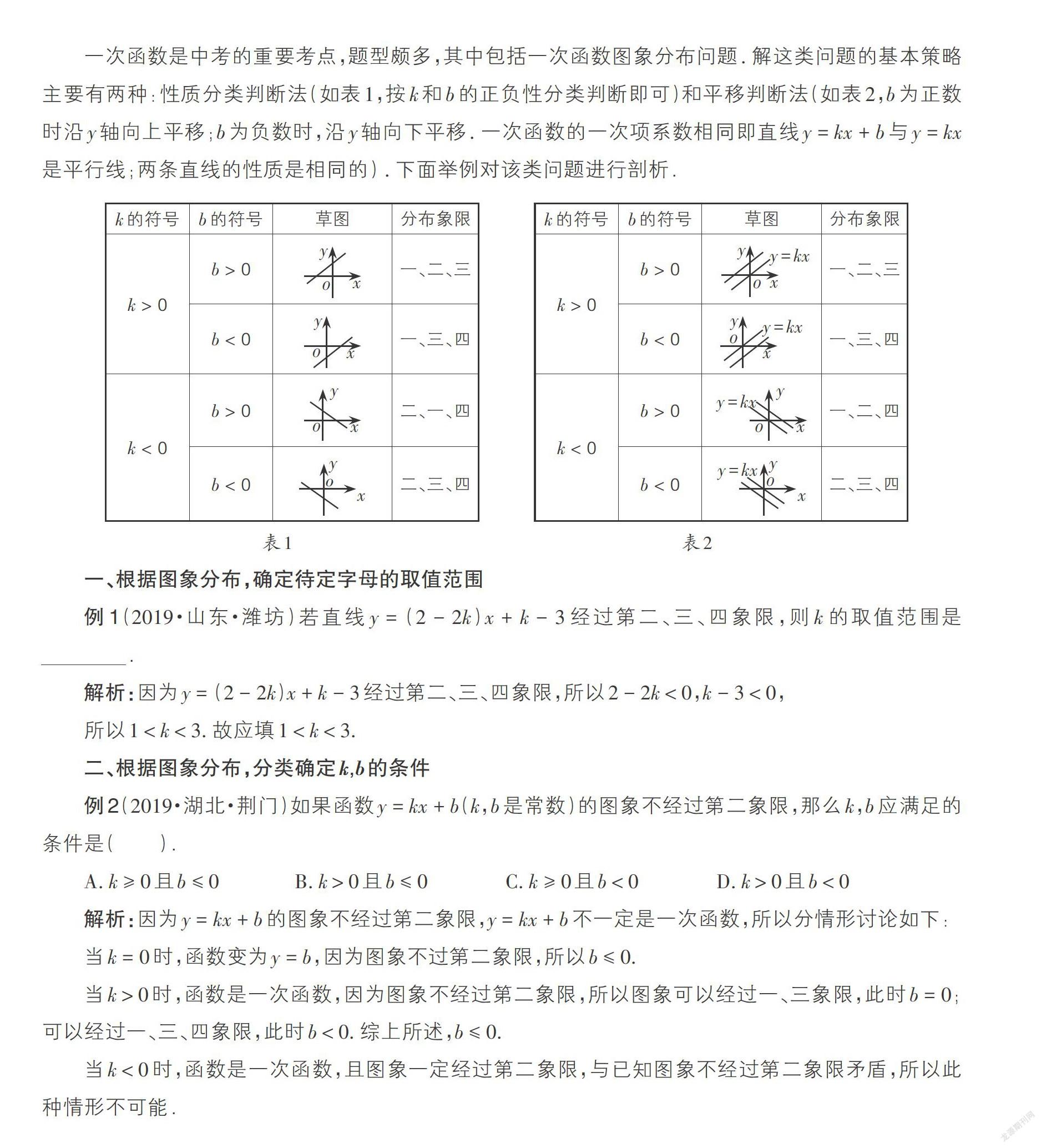

一次函数是中考的重要考点,题型颇多,其中包括一次函数图象分布问题. 解这类问题的基本策略主要有两种:性质分类判断法(如表1,按k和b的正负性分类判断即可)和平移判断法(如表2,b为正数时沿y轴向上平移;b为负数时,沿y轴向下平移. 一次函数的一次项系数相同即直线y = kx + b与y = kx是平行线;两条直线的性质是相同的) . 下面举例对该类问题进行剖析.
表1 表2
一、根据图象分布,确定待定字母的取值范围
例1(2019·山东·潍坊)若直线y = (2 - 2k)x + k - 3经过第二、三、四象限,则k的取值范围是 .
解析:因为y = (2 - 2k)x + k - 3经过第二、三、四象限,所以2 - 2k<0,k - 3<0,
所以1 二、根据图象分布,分类确定k,b的条件 例2(2019·湖北·荆门)如果函数y = kx + b(k,b是常数)的图象不经过第二象限,那么k,b应满足的条件是( ). A. k ≥ 0且b ≤ 0 B. k>0且b ≤ 0 C. k ≥ 0且b<0 D. k>0且b<0 解析:因为y = kx + b的图象不经过第二象限,y = kx + b不一定是一次函数,所以分情形讨论如下: 当k = 0时,函数变为y = b,因为图象不过第二象限,所以b ≤ 0. 当k>0时,函数是一次函数,因为图象不经过第二象限,所以图象可以经过一、三象限,此时b = 0;可以经过一、三、四象限,此时b<0. 综上所述,b ≤ 0. 当k<0时,函数是一次函数,且图象一定经过第二象限,与已知图象不经过第二象限矛盾,所以此种情形不可能. 综上所述,k ≥ 0且b ≤ 0. 故应选A. 三、根据图象分布,判断结论的正误 例3(2019·贵州·毕节)已知一次函数y = kx + b(k,b为常数,k ≠ 0)的图象经过一、三、四象限,则下列结论正确的是( ). A. kb>0 B. kb<0 C. k + b>0 D. k + b<0 解析:因为一次函数y = kx + b(k,b为常数,k ≠ 0)的图象经过一、三、四象限,所以k >0,b<0,所以kb<0. 故应选B. 四、根据k,b的正负性,综合推理判断 例4(2019·山东·临沂)下列关于一次函数y = kx + b(k<0,b>0)的说法,错误的是( ). A. 图象经过第一、二、四象限 B. y随x的增大而减小 C. 图象与y轴交于点(0,b) D. 当x>-[bk]时,y>0 解析:因为y = kx + b中k<0,b>0,所以图象经过第一、二、四象限,所以A正确;因为k<0,所以y随x的增大而减小,所以B正确;当x = 0时,y = b,所以图象与y轴的交点为(0,b),所以C正确;当y = 0时,x = -[bk],根据y随x的增大而减小,所以当x>-[ bk]时,y<0,所以D不正确. 故应选D. 五、变换待定字母的位置,判断函数在同一坐标系中的大致图象 例5(2019·浙江·杭州)已知一次函数[y1] = ax + b和[y2] = bx + a(a ≠ b),函数[y1]和[y2]的图象可能是( ). [O] [y][y1][y2][1][x] [y][y1][y2][1][x] [y][y1][y2][1][x] [y][y1][y2][1][x] [A][B][C][D][O][O] 解析:在選项A中,由直线[y1] = ax + b可知a>0,b>0,所以直线[y2] = bx + a经过一、二、三象限,所以A正确;在选项B中,由直线[y1] = ax + b可知a<0,b>0,所以直线[y2] = bx + a经过一、四、三象限,所以B错误;在选项C中,由直线[y1] = ax + b可知a<0,b>0,所以直线[y2] = bx + a经过一、四、三象限,所以C错误;在选项D中,由[y1] = ax + b可知a>0,b<0,所以直线[y2] = bx + a经过一、二、四象限,所以D错误. 故应选A. 六、根据图象平移,综合求解 例6(2019·湖南·邵阳)一次函数[y1=k1x+b1]的图象[l1]如下图所示,将直线[l1]向下平移若干个单位长度后得直线[l2],[l2]的函数表达式为[y2=k2x+b2]. 下列说法中错误的是( ). A. [k1] = [k2] B. [b1]<[b2] C. [b1]>[b2] D. 当x = 5时,[y1]>[y2] 解析:根据平移性质“直线平行,k值相等”,得[k1] = [k2];根据图象分布“位于y轴正半轴的b值较大”,可得[b1]>[b2];根据“横坐标相同时,直线x = a与直线的交点位置靠上的,其函数值较大”,可知当x = 5时,[y1]>[y2] . 故应选B.

