基于STEM教育理念的初中数学“综合与实践”一例

李雪琴 袁智强 戴飒英

摘要：基于STEM教育理念，以学生熟悉的折纸为研究载体，创设以航天为背景的现实情境，整合我国航天发展历程、平顶点折纸规律和“三浦折叠”的制作等内容，设计和实施《飞翔的数学》一课。由此得到数学“综合与实践”教学的启示：要关注生活与科学情境，选好研究的切入点;渗透数学知识与方法，凸显数学的应用价值;融入工程与技术元素，提升学生的课堂参与度。

关键词：STEM教育 综合与实践 折纸 三浦折叠 “6E”教学模式

數学“综合与实践”是一类以问题为载体、以学生自主参与为主的学习活动，是义务教育阶段数学课程的四大内容之一。在数学“综合与实践”活动过程中，学生从数学的角度出发，综合运用各领域的知识和方法，分析和解决生活中的问题。因此，数学“综合与实践”的教学具有学科性、综合性、实践性、主体性、过程性等特点。

STEM教育是一种以项目学习和问题解决为导向的课程组织方式。STEM教育具有跨学科性、情境性、体验性、趣味性等多个特征，其中，跨学科整合是STEM教育最核心的特征。STEM教育理念与数学“综合与实践”教学理念有相似之处。两者都强调要联系生活，创设现实情境，以问题为驱动，鼓励学生积极主动参与到教学活动中，培养学生的创新能力。不同之处在于，数学“综合与实践”教学主要关注数学与生活以及数学与其他学科之间的联系，而STEM教育跨学科整合的范围更广。所以，STEM教育理念可以作为初中数学“综合与实践”课程设计与实施的理论指导，为课程增添更丰富的跨学科元素。

基于以上想法，我们以STEM教育理念为指导思想，以学生熟悉的折纸为研究载体，创设以航天为背景的现实情境，整合我国航天发展历程、平顶点折纸规律和“三浦折叠”的制作等内容，设计和实施了《飞翔的数学》一课，引导学生从线段的数量关系和平行线、平行四边形等几何图形的角度认识、探究折纸，培养数感、符号意识、几何直观能力和模型思想，体会数学的应用价值。

一、教学设计

本课例基于“6E”教学模式，采用基于问题的学习方法。教学过程主要包括6个环节：情境引入（Engage）、折纸探究（Explore）、折纸解释（Explain）、模型制作（Engineer）、模型精致（Elaborate）和总结评价（Evaluate）。在教学过程中，创设以问题驱动的学习情境，引导学生发现、提出问题，并以小组合作的形式分析、解决问题。

第一步，了解我国航天事业的发展历。通过讲述我国成功发射的第一颗人造地球卫星“东方红一号”的故事，让学生充分融入情境，认识到航天是集科学、数学、技术、工程于一体的高科技领域之一，体会数学的应用价值。

第二步，探索卫星太阳能电池帆板易于收缩与展开的折叠方式，总结太阳能电池帆板的设计特点。从数学的角度探究太阳能电池帆板的折叠原理——平顶点折纸规律，经历从具体问题抽象为数学问题的过程，发展数感、符号意识，建立模型思想。

第三步，观察“三浦折叠”折痕展开图，用“线段平行”“平行四边形”“全等”“对称”等数学语言描述展开图的特征，培养几何直观能力。总结特征，设计“三浦折叠”的制作方案。

第四步，按照设计方案制作“三浦折叠”。发现折叠过程中出现的问题，分析问题，完成“三浦折叠”的制作，培养发现问题、提出问题、分析问题和解决问题的能力。

第五步，从大小、收缩形状等方面，在组内或组间比较制作的“三浦折叠”模型。分析问题产生的原因，设计并实施解决方案，优化“三浦折叠”模型。

第六步，回顾课程，进行总结性评价。分享学习感悟，巩固知识，提升思维。

二、教学流程

（一）情境引入：融入科学情境，了解航天发展

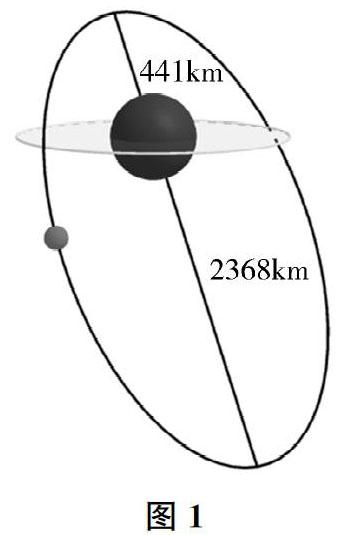
1.以2020年“中国航天日”主题宣传片引入，与学生分享“万户飞天”、中国航天第一个里程碑“东方红一号”卫星发射的故事，使用GeoGebra软件模拟演示“东方红一号”绕地飞行的示意图（如图1）。

2.科普卫星在生活中的应用，如电话通信、防控新冠肺炎疫情、驰援森林火灾、环境监测和气象监测等。

（二）折纸探究：提出工程问题，探索折纸规律

1.提出工程问题，激发学生思考：卫星的太阳能电池帆板以何种方式折叠能方便地打开？学生自发折叠、展开正方形纸张，模拟太阳能电池帆板的折叠与展开。之后，学生分享自己的折叠方式，根据收缩后的面积小、易于展开等标准评价学生的折叠方式。

2.学生了解依据折叠原理设计的卫星太阳能电池帆板的两种常见折叠方式：手风琴式（如图2）、旋转折叠式（如图3）。

3.学生小组合作，从折痕的数量关系入手，探索折纸规律，并进行实际操作。具体步骤如下：（1）在正方形纸张中任意画一个点A（如下页图4）;（2）经过点A将正方形纸张进行折叠，分别折叠1次、2次、3次、4次、5次、6次、7次……（3）以点A为起点，依折痕画射线，峰线（M）用实线表示，谷线（V）用虚线表示（如下页图5）;（4）填写表格并总结规律。

4.学生展示实验结果，并总结平顶点折纸规律。

师请每个小组派一位代表上台展示你们组的实验结果。

生（投影出示图6）我们发现实线数与虚线数的差为2，即M-V=2。我们还得出了各种线数与折叠次数之间的关系，表格中的n代表折叠次数，折叠n次，射线总数为2n，实线数为2n2+1，虚线数为2n2-1。当折叠次数多于一次的时候，实线数和虚线数都为奇数。

师很好！你们从填写的表格中总结了3条规律，并且通过具体的折叠次数推测出折纸的一般规律。

生（投影出示图7）我们组的射线总数是折叠次数的两倍，实线数和虚线数既有奇数，也有偶数，并按照自然数顺序排列。

生我们组折叠4次时，射线总数是12;折叠5次时，射线总数是16;折叠6次时，射线总数是20……从第2次以后，每折叠一次，射线总数增加4。

师这几组同学都得出了实线数与虚线数之差为2的结论，但射线的总数却各不相同。为什么会出现这么多种答案呢？到底谁的正确呢？请这几组同学分别介绍一下你们是如何得到这些结果的。

生我们组每次折叠都是经过点A对折，所以射线总数都比前一次增加一倍。

生我们组从第三次折叠开始，没有将每层纸全部翻折，经过点A，每次翻折共折痕的两层，（出示图8）所以每折叠一次，射线总数增加2。

生我们组从第3次开始，经过点A，每次折叠连续的四层，（出示图9）所以每次折叠，射线总数增加4。

生所以射线总数不同的原因是折叠的方法不同。虽然每次增加的折痕数不同，但都是偶数。

师经过折纸可以发现，每次折叠的折痕数最少增加2，最多增加2n（n为折叠次数）。所以，我们的结果都是正确的。实线数与虚线数有可能是奇数，也有可能是偶数。但经过点A，不管怎么折，射线总数始终为偶数。

生峰线的数量一定比谷线多吗？

生不一定！当顶点朝上的时候，峰线比谷线多;当顶点朝下的时候，原来的峰线变成了谷线，谷线变成了峰线，这时谷线比峰线多。

师在折纸中，没有绝对的峰线和谷线，而是取决于你观察的角度。

生经过点A，第一次折叠时，只有一条折痕，不满足M-V=2，所以这个结论是不是当折叠次数大于或等于2时才成立？

师很好的问题！事实上，我们可以将第一次折叠的折痕看作在同一条直线上的两条短折痕，即共端点反向的两条射线。所以，第一次折叠时，这个规律仍成立。（稍停）所以，我们可以从折痕的数量特征得到折纸的两个规律：在平顶点折叠中，实线数与虚线数的差为2，即峰线与谷线的数量差为2，|M-V|=2，这就是著名的折纸定理——前川定理;射线总数为偶数，即折痕总数为偶数，这是折纸中的均匀度定理。上述定理成立的前提是顶点在纸张内部。

5.分享折纸在生活中的妙用，如太空望远镜、折叠玩具、折叠机器人、安全气囊、心脏支架等。

（三）折纸解释：分析折叠特点，设计制作方案

播放“三浦折叠”制作视频，让学生观察“三浦折叠”的动态图和折痕图，通过折痕以及折痕形成的图形特征，分析并总结“三浦折叠”的特点，依据特点分析并设计“三浦折叠”的制作步骤。

师“三浦折叠”的展开有什么特点？

生沿纸张的对角线一次性展开。

师（出示图10）“三浦折叠”的折痕展开图有什么特点？

生除两端的边界外，由折痕形成的小格子是全等的平行四边形。

生“三浦折叠”展开的时候，由折痕形成的小格子形状、大小不变，是刚性折叠。

生每一个顶点处的折痕总数都为4，有的顶点有3条谷线和1条峰线，有的顶点有3条峰线和1条谷线，它们的差为2，满足前川定理，是平顶点折叠。

生横向折痕呈“直线形”，纵向折痕呈“波浪形”，横向折痕与纵向折痕都是峰线与谷线交替出现。

生“三浦折叠”是两个手风琴式折叠一横一纵的叠加。

师那如何制作“三浦折叠”呢？

生（出示图11）先把A4纸的宽平均分成5份，折叠成手风琴状。

师那纵向的波浪线折痕怎么折叠呢？

生用铅笔画出每一条波浪形折痕，用实线表示峰线，用虚线表示谷线。

师如果纸张再大一些，有更多的波浪形折痕，怎么办？大家再仔细观察一下，每相邻两行平行四边形的位置关系有何特点？

生每相邻两行的平行四边形关于横向折痕对称。

生所以，我们可以得出“三浦折叠”的制作方案：（1）将A4纸折成手风琴状，并收缩成细长条状;（2）将细长条的长平均分成7等分，在每个等分点上画虚实交替的等距平行线（如下页图12）;（3）将实线折成峰线，将虚线折成谷线（如下页图13）。

（四）模型制作：实施选定方案，制作“三浦折叠”

让学生小组分工合作，按照选定的方案制作“三浦折叠”，发现折纸不能一次性展开。让学生比较图13展开的折痕图与图10的折痕图，分析折痕的相同点与不同点，完成折纸。

师请大家打开手中的折纸，观察是否可以一次性将折纸展开？

生不能，展开的时候需要两步：先将折纸展开成细长条，再将手风琴式折纸展开。

师这说明我们的折纸还没有完成。请大家比较“三浦折叠”和自己手中折纸的折痕展开图，有什么相同点和不同点？

生这两种折痕展开图横向的折痕相同，但我们手中的同一条波浪形折痕不全是峰线或谷线，而是有一小段是峰线，有一小段是谷线。

师怎么将同一条波浪形折痕变为“全峰线”或“全谷线”呢？变的过程中要注意什么？

生将第一条波浪形折痕上的谷线折痕全变成峰线，第二条波浪形折痕上的峰线全变成谷线，以此类推。但波浪形折痕的峰线和谷线要交替出现。

师很好！折痕变化完成后，将纸张两端往中间推压，并重新将折痕压实，便得到了我们需要的“三浦折叠”。

（五）模型精致：分析问题成因，精致折纸模型

1.每个小组的成员相互比较制作的成品，分析制作成功与失败的原因。

师大家观察一下失败成品的折痕展开图，与成功成品的折痕展开图有什么不同？

生失败成品的折痕展开图中，由折痕形成的小格子是正方形，不是平行四邊形。

生（出示图14）原本应该在等分点处画倾斜的平行线，但实际上画了与细长条的长垂直的线段。

2.学生组内或组间相互比较制作成品收缩后的形状和大小，分析形状和大小不一致的原因，并根据具体的原因完善折纸模型，使制作的“三浦折叠”收缩后的面积小、易于展开。

师把自己制作的“三浦折叠”与其他同学的比较一下，看收缩以后的形状和大小是否一致？

生（出示图15）我们组有的同学制作的“三浦折叠”收缩以后，峰线和谷线分别在同一条直线上，（出示图16）也有的同学制作的“三浦折叠”不在同一条直线上。

师这是什么原因呢？

生我们组的是因为画的平行线不平行。

生我们组的是在折叠时，画的实线和虚线没有与折痕完全重合。

师所以，在折叠时必须满足等距以及平行线与折痕重合两个条件。

生我们组折叠的大小不一样，通过对比发现，“三浦折叠”收缩以后的大小与平行线倾斜的角度有关。平行线与细长条的长倾斜的角度越大，收缩后的面积越小;倾斜的角度越小，收缩后的面积越大。

师影响“三浦折叠”收缩后的面积的主要因素就是平行线倾斜角的大小。三浦公亮经过研究发现，要满足易于收缩、展开以及收缩后面积最小这两个条件时，倾斜角为83°最适宜。

3.完善模型和完成评价后，用GeoGebra软件模拟“三浦折叠”型的太阳能电池帆板在太空中的折叠与展开。

（六）总结评价：反思探究过程，促进思维提升

引导学生回顾学习过程以及课堂表现，进一步巩固知识、提升思维。依据学生在课堂中提出问题、解决问题、小组合作等方面的表现进行客观评价。

三、总结与启示

（一）关注生活与科学情境，选好研究的切入点

本课选择“三浦折叠”作为探究的切入点，理由有三：（1）“三浦折叠”是一种简单但又具有挑战性的折纸方式;（2）“三浦折叠”同时蕴含了简单和复杂的数学原理，可以选择难度适宜的数学知识进行教学;（3）“三浦折叠”应用于卫星太阳能电池板的折叠设计，能为课程提供丰富的科学情境和生活情境。可见，在选择数学“综合与实践”的课题时，应该打破数学与生活以及其他学科的边界，积极寻找数学与生活以及其他学科的交汇点，作为研究的切入点。

（二）渗透数学知识与方法，凸显数学的应用价值

本课中，通过讲述“东方红一号”卫星解决“抓得住”的技术问题，让学生知道测量卫星到地面的距离可以抽象为一个数学问题，让学生感受数学抽象的思想方法，同时体会数学在航天中的应用价值。平顶点折纸规律的探索，则让学生经历了数学建模的过程。因此，数学“综合与实践”的课程内容，应该渗透数学知识、思想与方法，凸显数学的应用价值。

（三）融入工程与技术元素，提升学生的课堂参与度

工程实践环节需要学生依据设计方案动手操作，可以让学生充分发挥自己的创造性，完成作品制作。教师引导学生使用信息技术手段解决问题，将问题变得更加可视化，从而更为深入地理解知识，体会科学技术给生活和学习带来的便利。比如，学生制作“三浦折叠”的过程——总结“三浦折叠”的特点、设计制作方案、动手实践，充分调动了学生参与的积极性。因此，在数学“综合与实践”的教学中，融入工程与技术的实践环节，是提升学生课堂参与度的有效措施。

*本文系教育部人文社会科学研究青年基金项目“创新型STEM教师培养的探索性研究”（批准号：18YJC880115）的阶段性研究成果。本刊曾在2019年第3期、第8期和2020年第4期呈现其系列研究成果。

参考文献：

[1] 张伟俊.数学“综合与实践”活动的有效设计研究[J].上海教育科研，2018（10）.

[2] 蔡庆有.数学“综合与实践”内容的课程分析[J].教学与管理，2017（1）.

[3] 相春艳.初中数学“综合与实践”课程实施现状的调查研究[D].扬州：扬州大学，2014.

[4] 余胜泉，胡翔.STEM教育理念与跨学科整合模式[J].开放教育研究，2015（4）.

[5] 梅浩，袁智強，郑柯.基于数学实验的STEM教育——以“探究金属的冷却模型”为例[J].教育研究与评论（中学教育教学），2019（3）.

[6] 托马斯·赫尔.折纸设计的秘密——折纸模型中的数学世界[M].张文娟，叶雅玲，译.北京：机械工业出版社，2017.