一道中考反比例函数试题的解法探究
祝明基


[摘 要] 一份好的中考试卷应该与考试说明要求相吻合,知识点覆盖合理;贴近教材,应用性和开放性适度;突出数学知识的基础性和综合性;主干知识考查到位,核心知识重点考查;注重“双基”,侧重能力评价;以人为本,促进学生发展. 全卷应充分体现新课程标准的评价理念,试卷中所渗透出的教育信息既要对今后初中数学教学起到良好的导向作用,又应体现选拔功能.
[关键词] 反比例函数;中考;试题解法
试题呈现
试题如图1,函数y=x的图像与函数y=■的图像在第一象限交于点B,点C是函数y=■在第一象限图像上的一个动点. 当△OBC的面积为3时,点C的横坐标为______.
试题考查要点分析
本题是一道创新题,入口低,具有多种解题方法,体现了命题的层次性,是一道老題新做. 此题考查了反比例函数与一次函数的交点问题,涉及的知识有反比例函数中k的几何意义,梯形、三角形的面积求法,坐标与图形性质,解方程,相似三角形等. 考查分类讨论思想,分类讨论时注意不重不漏,考虑问题要全面. 据了解,该题在桂林全市的得分相当低,难度系数只有0.18,在全卷中算是一道小综合题,具有很强的选拔功能.
试题解法探究
按分类思想,点C的位置有两种情况:在直线OB的左边或右边. 本题的解法主要分为如下两大类型.
1. 面积变换法
(1)填补法
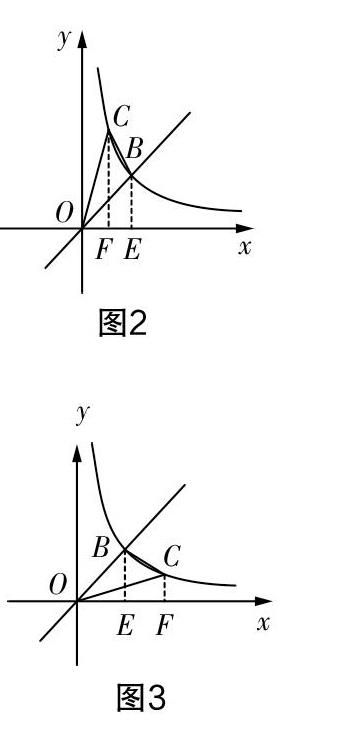
当点C在直线OB左边时,如图2,过点C作CF⊥x轴,过点B作BE⊥x轴,垂足分别为F,E. 联立y=x与y=■可求得B(2,2). 由函数y=■图像上的点的几何意义可得△OCF与△OBE的面积均为2,又△OBC的面积为3,所以S■+S■= S■+S■=5. 由条件令Cc,■,则有2+■·■+2·(2-c)=5,解得c=-4(舍去)或c=1,此时c=1.
当点C在直线OB右边时,如图3,过点C作CF⊥x轴,过点B作BE⊥x轴,垂足分别为F,E. 同理可求出c=-1(舍去)或c=4.
综上可知,满足条件的点C的横坐标为1或4.
(2)分割法
如图4,当点C在直线OB的右边时,过点B作BD⊥x轴,CH⊥x轴,垂足分别为D,H,BD交OC于点E. 易求得B(2,2),S■=S■+S■=■BE·OH. 令Cc,■,由△ODE∽△OHC,得■=■,即■=■,所以DE=■. 所以3=■·2-■·c,解得c=4或c=-1(舍去). 同理,当点C在直线OB的左边时,c=1. 综上可知,满足条件的点C的横坐标为1或4.
(3)等积法
容易求得B(2,2). 当点C在直线OB的右边时,过点B作BD⊥x轴,CH⊥x轴,垂足分别为D,H,BD交OC于点E,如图5. 因为S■+S■=S■+S■,又S■=S■=2,所以S■=S■. 由条件设Cc,■,则3=■·■+2·(c-2),解得c=4或c=-1(舍去). 同理,当点C在直线OB的左边时,可求得c=1. 综上可知,满足条件的点C的横坐标为1或4.
(4)构造三角形法
当点C在直线OB的右边时,如图6,过点C作CD⊥x轴,与x轴交于点D,与直线OB交于点H,则S■=S■-S■. 容易求得B(2,2),令Cc,■,则H(c,c),HC=c-■. 所以3=■·c-■c-■·c-■(c-2)=c-■,解得c=4或c=-1(舍去). 同理,当点C在直线OB的左边时,可求得c=1. 综上可知,满足条件的点C的横坐标为1或4.
2. 函数解析法
当点C在直线OB的右边时,如图7. 过点C作直线CD∥OB交x轴于点D,过点B作BE⊥x轴,垂足为E,过点D作DH⊥OB,垂足为H,过点C作CN⊥OB,垂足为N. 因为B是直线OB与双曲线的交点,所以B(2,2). 所以OB=2■. 由S■=■OB·CN得3=■×2■×CN,所以CN=■. 所以DH=■. 在Rt△DOH中,因为∠DOH=45°,所以OH=DH=■,OD=3. 所以点D的坐标为(3,0). 因为CD∥OB,所以可设直线CD的解析式为y=x+b,将(3,0)代入后可解得b=-3,所以直线CD的解析式为y=x-3. 联立y=■,y=x-3, 可解得x=4或x=-1(舍去). 所以此时满足条件的点C的横坐标为4.
当点C在直线OB的左边时,如图8,过点C作直线CD∥OB交y轴于点D,分别过点C和点D作直线OB的垂线段. 同上述解法,可求得点D的坐标为(0,3),于是直线CD的解析式为y=x+3. 联立y=■,y=x+3, 解得x=1或x=-4(舍去). 所以此时满足条件的点C的横坐标为1.
综合可知,满足条件的点C的横坐标为1或4.
教学建议
1. 强化对反比例函数中k的几何意义的理解,熟悉基本图形,熟悉基本技能的应用. 例如,如图9,A是反比例函数y=■(x>0)图像上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C. 若四边形OBAC的面积为3,则k的值为______.
2. 函数图像上的点的表示尤为重要. 在教学中,应引导学生将点的坐标转化成相关线段的长,再用几何知识解题.
3. 教学中应渗透试题的变式训练. 学生能自己命题是复习的最高境界.
4. 教学中应加强学生知识综合能力的提升,强化数形结合思想方法.
5. 注重一题多解和多题一解相结合,前者注重挖掘题型的功能——多角度、全方位地理解试题,强调思维的多向性;后者注重训练学生的归纳能力.

