考虑延时效应的供应链质量决策

周熙登，徐 兵，江玮璠，胡启帆

(1.南昌大学 管理学院管理科学与工程博士后流动站，江西 南昌 330031；2.南昌大学 管理学院，江西 南昌 330031；3.南昌工程学院 工商管理学院，江西 南昌 330099)

1 问题的提出

如今的市场竞争越来越激烈，制造商和零售商均积极采取不同质量策略，以获得更大的市场生存空间。制造商可以通过设计、制造等环节来提高产品质量，零售商可以通过提供良好的售前咨询服务、体验式购物环境以及完善的售后服务等方式来提高服务质量。另外，企业竞争不是单一企业之间的竞争，而是供应链之间的竞争，因此制造商和零售商在质量上的合作对双方获得更大的竞争力显得尤为重要。

近年来，关于产品质量的报道并不鲜见，这也引起了学术界对供应链质量问题的关注。Boyaci等[1]考虑两条竞争的供应链，而且两条供应链均由一个供应商和一个零售商组成，研究了供应链间的3种竞争情形，得到每种情形下的质量均衡策略；Zhu等[2]考虑贴牌生产的供应链，卖买双方共同承担与质量相关的商誉成本、售后服务成本和市场份额损失成本，探讨了提高产品质量的决策问题；Gurnani等[3]构建了产品质量和营销努力的需求函数，比较了3种不同的供应链契约形式；Chenavaz[4]和He等[5]研究了消费者具有参考质量行为的企业动态质量决策。

但斌等[6]针对二级供应链构建了基于质量的需求函数，研究了不同决策情形下的质量决策问题；朱立龙等[7]针对制造商为主导的三级供应链结构模型，研究了不同激励机制下制造商的质量决策问题；肖迪等[8]研究了供应链4种决策情形(集中决策、供应商合作、供应商不合作、混合情景)下的质量和价格均衡策略解，以及质量竞争程度对不同情形下供应链策略解的影响；唐润等[9]考虑保鲜努力水平对生鲜食品质量的影响，研究了生鲜食品供应链双渠道下的协调机制。另外，也有学者从非理性的角度进行研究，刘云志等[10]考虑下游零售商具有损失规避偏好，研究了集中和分散情形下的供应链质量决策。上述研究考虑了供应链上游制造商或供应商通过设计产品质量影响顾客需求，没有考虑零售端通过提高服务质量水平促进销售的问题。

针对零售商服务质量水平问题的研究也得到了众多学者的关注。Tsay等[11]研究了有容量限制的价格和服务竞争的动态模型；Ren等[12]和Dan等[13]均在网络渠道和实体渠道供应链中考虑了服务竞争问题。另外，还有Shi等[14]、Ali等[15]学者将服务和供应链成员结合起来，探讨了服务质量水平问题。国内也有不少学者对供应链服务质量水平进行研究。张振政[16]在双渠道供应链模型中探讨了服务竞争策略问题；秦星红等[17]研究了网络零售商和第三方物流企业供应链的服务质量协调问题；周维浪等[18]考虑消费者的购买行为，分析了集中化、分散化制造商主导和零售商主导型3种决策下，新产品与再制造产品的定价和服务水平决策及协调问题；张学龙等[19]探讨了同时拥有网络和实体的零售商，研究了扰动情形下的服务决策问题。

提高产品质量是企业的生存之道与发展的基础，如何将产品有效地传递给用户，在一定程度上也需要高质量的服务水平，高质量的产品和服务对企业提高绩效、增强竞争力非常重要。本文将产品质量和服务质量作为决策变量放在同一框架下进行研究，探寻产品质量和服务质量的均衡策略，具有现实意义。本文通过分析已有文献发现，虽然供应链的产品质量策略问题和服务质量策略问题已经引起众多学者的关注，但是从供应链的视角将产品质量—服务质量策略结合起来研究的文献较少，黄甫等[20]分析了供应链产品质量和服务质量的均衡策略问题，然而其研究仅处于静态框架下。

关于延迟效应的研究文献较少，陈东彦等[21]假设产品品牌信誉受广告延时效应影响，研究了集中和分散决策下供应链的广告最优均衡策略问题。本文基于质量对商誉的延时效应，研究供应链产品质量水平和服务质量水平决策问题。质量对商誉的延时效用指产品质量和服务质量的变化对商誉的影响不是立竿见影，而是经过一段时间才能体现。因为消费者购买、体验完产品后才可能对商品进行评价和宣传，所以质量提高的商誉效应有一段时间的滞后期。表1总结了近期相关研究最新文献的主要特征，并与本文进行了比较。

表1 最近相关文献特征对比

续表1

鉴于此，本文考虑产品质量水平和服务质量水平对商誉影响的延迟效应，研究基于延迟效应的动态产品质量水平和服务质量水平决策问题。首先，基于Nerlove-Arrow模型建立产品质量和服务质量对商誉影响的延迟微分方程，利用极大值原理构造制造商和零售商Hamilton函数，求解不同决策下的最优产品质量水平和服务质量水平，以及分散式决策下的制造商最优服务质量成本分担率，并提供采用哪种决策类型的判断条件，最后采用数值分析来分析延迟时间对供应链利润、产品商誉、产品质量水平、服务质量水平等的影响。

2 基本假设及符号说明

本文研究的对象是二级供应链，由一个制造商和一个零售商构成。制造商为供应链上的核心企业，并通过研发、运用新技术、改造制造工艺流程等方式提高产品质量；零售商通过提供良好的售前服务咨询、体验式购物环境、售后退换货服务等方式提高产品的服务质量水平。制造商为了激励下游零售商提高服务质量水平，愿意承担其部分或者全部服务成本。假设φ(t)(0≤φF(t)≤1)为t时刻制造商承担零售商服务质量成本的比例。

假设1制造商产品质量水平和零售商服务质量水平共同正向影响产品商誉，基于Nerlove-Arrow[22]模型，构建质量水平影响产品商誉的延迟微分方程

(1)

G(0)=G0。

假设2零售商服务质量水平和制造商产品质量水平直接影响市场需求，同时服务质量水平和产品质量水平通过作用于商誉间接影响市场需求，构建产品市场需求函数

D(t)=a+bG(t)+θZ(t)+μS(t)。

(2)

(3)

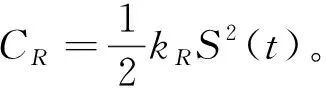
(4)

相关符号及说明如表2所示。

表2 相关符号及说明

本文还假设供应链成员是以无限时区内各自利润最优进行决策。综上所述，可以得到制造商、零售商及整个供应链的净贴现利润函数分别为：

(5)

(6)

(7)

本文相关变量之间的关系如图1所示。

3 分散式决策

作为独立的个体，制造商和零售商以自己利益最优为原则，分别对产品质量水平和服务质量水平进行决策。同时，为了扩大市场规模，制造商鼓励零售商提高服务水平，承诺会分担零售商一定比例的服务质量改进成本。

命题1在分散式决策情形下，制造商最优产品质量水平和零售商最优服务质量水平分别为：

产品的最优商誉为

制造商分担零售商服务质量成本的最优比例为

证明首先，假设制造商分担零售商服务质量成本比例为一既定值φ，以此求解制造商和零售商的最优质量水平。

利用极大值原理，构造Hamilton函数

HM=e-λt{pM[a+bG(t)+θZ(t)+μS(t)]-

dz(t))+βS(t-ds(t))-δG(t)]。

(8)

令

(9)

(10)

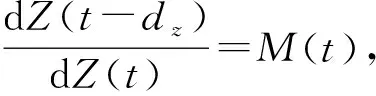
(11)

(12)

根据文献[21]，M(t)=φ(t-dz,t)=eδdz，因此

(13)

由式(13)可以判断c=0，重新整理，得到制造商最优质量水平为

(14)

利用极大值原理，构造Hamilton函数

HS=e-λt{pR[a+bG(t)+θZ(t)+μS(t)]-

βS(t-ds(t))-δG(t)]。

(15)

类似地，求得零售商的最优服务质量水平为

(16)

将式(14)和式(16)代入式(1)，得到

(17)

其次，制造商设计服务质量成本的最优分担比例。将式(14)、式(16)和式(17)代入式(5)，化简得

[pMa+pMθZ+pMμS]。

将JM对φ求最大值，得到制造商的最优服务质量改进分担比例

由命题1可知，当存在服务合作时，制造商和零售商的最优利润分别为：

(18)

(19)

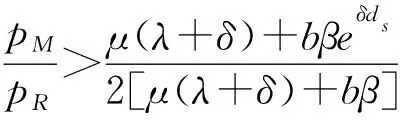
推论1说明边际利润的大小对企业进行质量投入决策的影响很大，边际利润越大，企业提高质量水平的积极性越高。制造商的边际利润越大，支持零售商提高服务质量水平的积极性越高；边际利润越小，服务质量水平的支持力度越低。制造商承担了部分服务质量投入成本，在一定程度上降低了下游零售商的经济负担，能够促使其提高服务质量。零售商提升服务质量影响商誉的延迟时间越长，产生的投入成本越多，带来的经济回报越滞后，会在一定程度上降低制造商承担服务质量投入的积极性。

推论3分散式决策下，延迟时间越长，相应的制造商最优产品质量水平和零售商最优服务质量水平越高；制造商最优利润函数随产品质量水平延迟时间的增加而减少，随服务质量水平延迟时间的增加而增加；零售商的最优利润函数随服务质量水平延迟时间的增加而减少，随产品质量水平延迟时间的增加而增加。

推论3说明产品质量水平影响商誉的延迟时间越长，制造商在产品研发、技术引进等的投入就越多，从而增加了企业的成本，虽然市场需求有所提高，但是所获得的利润降低，同时产品质量水平影响市场需求，提高产品质量有助于增加零售商的销售收入，使其利润增加。另一方面，服务质量水平影响商誉的延迟时间较长虽然能够提高服务质量水平，但是增加了成本负担，降低了零售商的利润。由于延迟效应的影响，制造商降低零售商服务质量改进成本分担比例(命题1)，以减轻成本压力，另外改进服务质量水平能够在一定程度扩大产品的市场规模(式(2))，从而增加制造商的利润。综上所述，服务质量改进影响商誉的延迟时间越长，越有利于制造商，越不利于零售商。

4 集中式决策

在集中式决策下，制造商和零售商被看做是一个企业里面的两个部门，通过设计最优的产品质量Z(t)和服务质量S(t)来实现供应链利润的最大化。

命题2在集中式决策下，制造商最优产品质量水平和零售商最优服务质量水平分别为：

产品的最优商誉为

结合式(1)，利用极大值原理构造Hamilton函数

HMR=e-λt{(pM+pR)[a+bG(t)+θZ(t)+

κc(t)[γZ(t-dz(t))+βS(t-ds(t))-δG(t)]。

(20)

令

(21)

(22)

HMR关于Z(t)和S(t)的Hessian矩阵为

因为一阶顺序主子式小于0，二阶顺序主子式大于0，所以T(HMR)矩阵是负定的，(Z**(t)，S**(t))为JMR的唯一最优解，即为制造商和零售商的最优质量水平。类似于命题1的求解过程，得到：

(23)

(24)

将式(23)和式(24)代入式(1)，得到

(25)

由命题2进一步求得整个供应链的最优利润为

(26)

命题3集中决策下的制造商最优产品质量水平、零售商最优服务质量水平、产品最优商誉和市场需求分别大于分散决策，即Z**(t)>Z*(t)，S**(t)>S*(t)，G**(t)>G*(t)和D**(t)>D*(t)。

证明由

(27)

得到Z**(t)>Z*(t)，由

(28)

得到S**(t)>S*(t)。

将分散决策和集中决策下的商誉进行比较：

[γ(Z**-Z*)+β(S**-S*)]。

(29)

由式(27)和式(28)得到G**(t)>G*(t)，由式(26)～式(28)得到集中决策下的产品市场需求大于分散决策情形，即D**(t)>D*(t)。

命题3说明，供应链采用集中式决策模式可以激励制造商和零售商提高质量水平，进而促进产品销售和品牌商誉的积累。

命题4

(1)当延迟时间满足ds∈RS1且dz∈RZ1，或者ds∈RS2且dz∈RZ3时，集中式决策下供应链的整体利润不小于分散式决策，集中决策是供应链的最优决策模式。

(2)当延迟时间满足ds∈RS1且dz∈RZ2，或者ds∈RS2且dz∈RZ4时，分散式决策下供应链的整体利润大于集中式决策，供应链应采取分散决策模式。

(3)当延迟时间满足ds∈RS3时，分散式决策下供应链的整体利润不小于集中式决策，分散决策是供应链的最优决策模式。

即

证明

(30)

整理式(30)得到

J(dz,ds)=JMR-JM-JR=A1f1(dz)-

A3f1(dz)2+A2f2(ds)-A4f2(ds)2。

(31)

同时，令y1=A1f1(dz)-A3f1(dz)2，y2=A2f2(ds)-A4f2(ds)2。

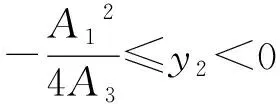
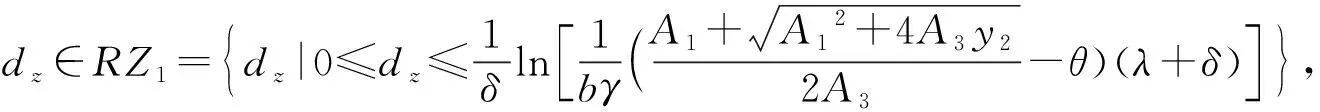
命题4说明延迟时间给供应链成员选择决策方式提供了依据。根据产品质量水平对商誉影响的延迟时间和服务质量水平对商誉影响的延迟时间的取值范围，采用不同的决策方式。当供应链成员双方采取集中决策时，若制造商和零售商能够签订利润合理分配协议，则会使制造商和零售商的最优利润得到Pareto改善。

5 数值分析

本章通过数值实验，分析供应链利润、产品商誉和质量水平3方面在分散式决策和集中式决策两种情形下的差异，以验证前文理论。

假设模型中各参数的取值分别为：贴现率λ=0.1，衰减δ=0.01，边际利润PM=10和PR=4，影响因子b=1.2，θ=3，μ=2，γ=2，β=1，kM=1，kR=1，品牌信誉初值G(0)=2，市场潜在销售量a=2。

首先，根据基准参数，取dz=1，ds=1，t∈[0,200]，绘制集中决策和分散决策下产品商誉的最优轨迹，如图2所示。

由图2可见，随着时间的推移，集中决策下的产品商誉高于分散式决策，两种情形下商誉值之间的差距越来越大且趋于稳定。

其次，根据基准参数绘制分散式和集中式决策下延迟时间分别对制造商产品质量水平和零售商服务质量水平的影响，如图3和图4所示，图中横坐标分别为产品质量影响商誉的延迟时间和服务质量影响商誉的延迟时间。

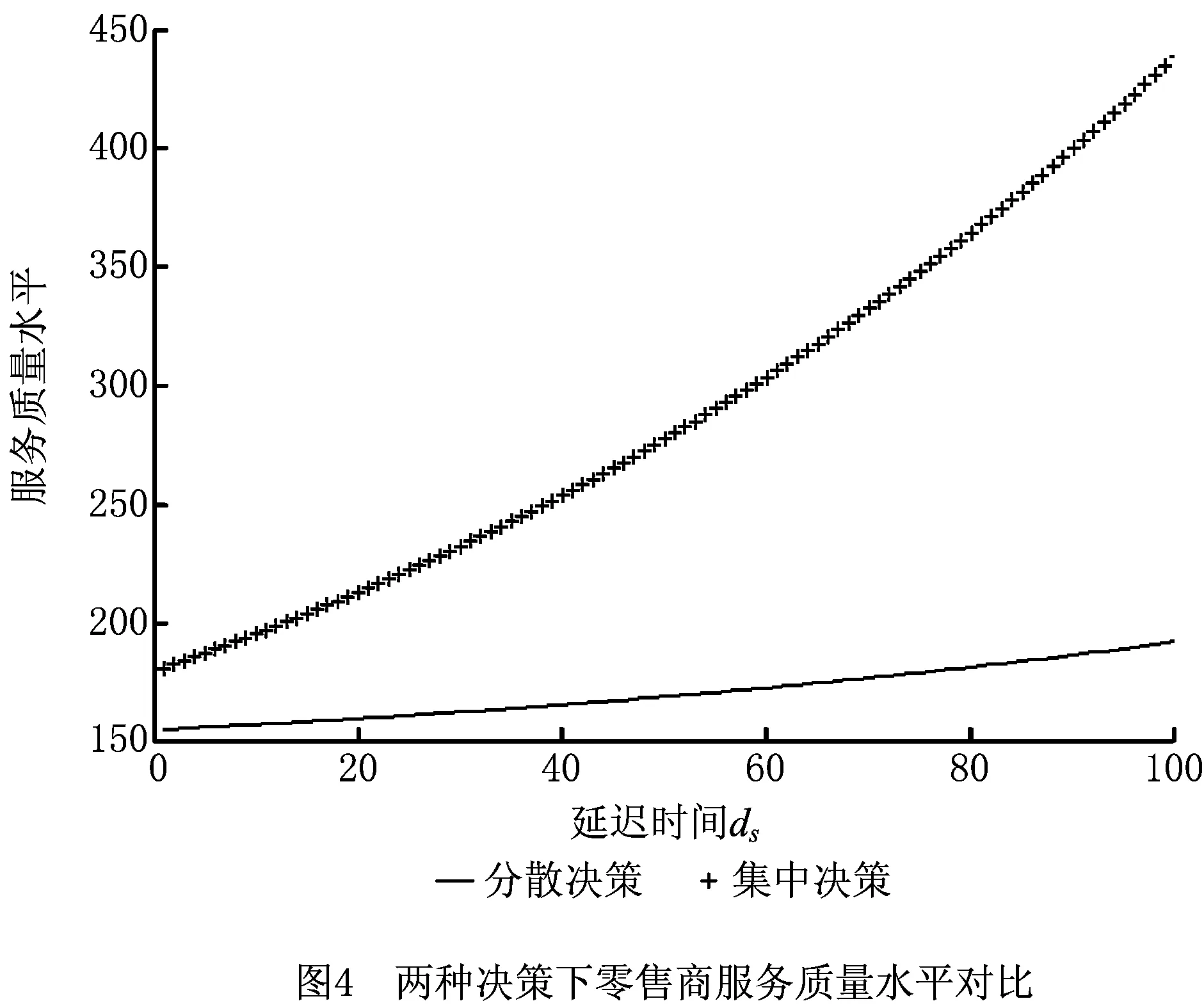
由图3和图4可知，集中式决策下制造商的产品质量水平和零售商的服务质量水平均高于分散式决策。两种决策下制造商的产品质量对商誉影响的延迟时间越长，制造商的投入程度越高，说明延迟时间能激励制造商进行更多的产品质量改进，从而提高产品质量水平；同样，服务质量影响商誉的延迟时间越长，越能激励零售商进行服务质量改进，从而提高服务质量水平。

在分散决策下绘制制造商和零售商利润随延迟时间dz变化的情况(ds=1，dz∈[0,100]，如图5a)，以及制造商和零售商利润随延迟时间ds变化的情况(dz=1，ds∈[0,100]，如图5b)。

由图5可知，分散决策下制造商利润随产品质量延迟时间的增加而减少，零售商利润随产品质量延迟时间的增加而增加，因此产品质量延迟效应对零售商有利而对制造商不利；分散决策下制造商利润随服务质量延迟时间的增加而增加，零售商利润随服务质量延迟时间的增加而减少，因此服务质量延迟效应对零售商不利而对制造商有利。

最后，取ds=1，dz∈[0,80]，绘制两种决策下供应链利润随产品质量延迟时间变化的情况(如图6a)；取dz=1，ds∈[0,100]，绘制两种决策下供应链利润随服务质量延迟时间变化的情况(如图6b)。

由图6a得知，与分散决策相比，当产品质量延迟时间比较短时，集中式决策下制造商的产品质量改进得越多，整个供应链获得的利润越多，此时制造商和零售商更倾向于集中式决策；当产品质量延迟时间较长时，在集中决策下将会促进制造商改进产品质量，提高产品质量水平，但会增加制造商成本，降低整个供应链的利润。因此，当产品质量延迟时间超过一定范围时，分散式决策所获得的利润大于集中决策。

从图6b可见，当服务质量延迟时间在一定范围内时，集中式决策下零售商服务质量改进得越多，供应链利润越大，若制造商制定合适的利润分配比例，零售商则会接受集中式决策；当服务质量延迟时间超过该范围时，增加延迟时间意味着集中决策下服务质量改进得更多，导致集中决策下的制造商和零售商成本增加。因此，当服务质量延迟时间比较长时，供应链成员将采用分散式决策。

6 结束语

本文在现有文献基础上，考虑产品质量和服务质量对商誉的影响存在一定延迟时间，构建了基于延迟效应的微分博弈模型，比较了分散和集中两种决策模式下的最优产品质量水平、最优服务质量水平、产品商誉和供应链整体利润，研究了延迟时间对供应链成员利润和质量水平的影响，得到以下结论：

(1)对于产品商誉、产品质量水平和服务质量水平而言，集中式决策获得的最优值高于分散式决策，但是不同于以往研究的结论，集中式决策下的供应链整体利润并非总是优于分散式决策，两种情形下整体利润的大小与产品质量延迟时间和服务质量延迟时间有关。

(2)当产品质量延迟时间增加时，制造商最优利润减少，零售商最优利润增加；当服务质量延迟时间增加时，制造商最优利润增加，零售商最优利润减少，即产品质量延迟时间与制造商最优利润负相关，与零售商最优利润正相关，服务质量延迟时间与制造商最优利润正相关，与制造商最优利润负相关。

(3)产品质量延迟时间与质量改进正相关，随着延迟时间的增加，制造商会提高产品质量水平，服务质量延迟时间能够有效刺激零售商改进服务质量，提高服务水平。然而，在一定范围内，随着服务质量延迟时间的增加，制造商参与零售商改进服务质量的意愿降低。

(4)两种决策下，产品商誉随时间递增，并趋于稳定值，集中决策下的商誉值大于分散决策下的商誉值。

因此，作为供应链主导者的制造商应该根据延迟时间的取值范围，选择不同的合作模式，并考虑在合作情形下如何设计利益机制来实现供应链成员双赢。未来可以对零售商服务竞争情形下的供应链决策、制造商质量竞争情形下的供应链决策，以及延迟效应对供应链决策的影响进行研究。