基于BP神经网络与非参数核密度估计的短期风电功率概率区间预测

熊 鸣

(北京信息科技大学 自动化学院，北京 100192)

0 引言

近几年，随着大规模风电并网，风力发电的随机性和波动性对电力系统稳定运行的影响越来越大。提前预测风电场发电量，为电网调度提供发电规律，有助于减轻风电对电网造成的威胁。短期风电功率预测是预测未来72 h的发电量，其结果可用于制定日前发电计划、合理调度电网资源、优化冷热备用等工作[1]。因此研究短期风电功率预测具有重要意义。

目前短期风电功率预测主要有物理方法、统计方法和学习方法[2]。这些方法在短期风电功率预测中各有优缺点，在预测过程中一般根据风电场历史数据的特点进行方法的选取。文献[3]指出，目前的短期风电功率预测均方根误差大约为10%～15%。

这些方法的预测都是确定性预测，其预测结果只是给出了未来该风电场可能出现的确切功率值，无法估计出该确切值出现的概率以及风电功率可能出现的波动范围。文献[4]指出，确定性预测不能全面描述出风电场发电规律，其预测结果不能准确支持电力部门制定发电计划和调度等工作，因此有必要对未来风电功率波动范围进行预测研究。

目前一些学者已经开展了一些功率区间预测研究。例如文献[4]中总结了一些已经在风电概率预测中出现的方法，有高斯分布、β分布、t分布、α-稳定分布等。这些方法实现简单，但缺点是当预测误差不满足某一特定分布时，预测结果将出现较大偏差。另外，分位点回归法也被应用于风电概率预测中，文献[5-7]都应用了该方法，该方法的优点是不用提前假设分布，但缺点是对数据质量要求较高。此外在文献[8]中，作者利用极限学习机算法不通过点预测结果直接得出了风电功率预测区间；文献[9]、文献[10]、文献[11]分别采用稀疏贝叶斯、小波神经网络算法、Bootstrap法成功进行了风电概率预测。

非参数核密度估计是一种以实际误差概率分布为基础构建的方法，优点是可以对一些特定条件进行统计分析，且在分析过程中只对数据本身分布的特征进行研究，不会对数据分布添加任何假设，具有良好的预测效果。该方法已成功应用于负荷概率预测中[12]，考虑到风电功率概率预测也适用，故本文在点预测的基础上采用非参数核密度估计对风电功率进行概率区间预测。在给定置信度情况下，预测出风电功率波动上下限，并以我国依兰风电场为实例进行分析、验证。

1 风电功率点预测

1.1 NWP风速修正

数值天气预报(numerical weather prediction，NWP)数据作为短期风电功率预测模型必要输入量，其数据准确性直接关系到预测功率的精度。其中，NWP风速是影响风电功率预测准确性的主要因素。功率P与风速v具有3次方的正比关系：

(1)

式中:Cp为风能利用系数；A为风轮扫过面积；ρ为空气密度。

图1为依兰风电场某日的NWP风速和实际风速对比曲线。从图中可以看出，NWP风速范围为0～5.5 m/s，实际风速范围为0～11 m/s。NWP数据中的预测风速与实际风速之间的误差较大，最大差值可达6.86 m/s。如果直接将NWP风速作为点预测模型的输入量，势必会产生较大的误差。为提高点预测精度，在构造风电功率点预测模型前，需对依兰风电场的NWP风速进行修正。

本文采用拟合修正法和BP神经网络法进行修正。

拟合修正法是根据训练样本数据，拟合出归一化NWP风速v与修正风速f(v)的关系表达式，然后根据该表达式计算出测试样本的修正风速。

BP神经网络修正法是将v作为BP模型的输入量，归一化的实际风速值vt作为模型期望输出量；隐含层设置为单隐含层，神经元数目根据经验公式(2)确定取值范围；经不断学习，利用训练好的模型，预测出修正风速。

(2)

式中：m为隐含层神经元数目；a为调节系数，在1～10之间；n和l分别为输入层和输出层的神经元数目，由于输入量和输出量数目为1，故n、l取1。

修正结果精度采用归一化绝对平均误差(normalized mean absolute errror，NMAE)和归一化均方根误差(normalized root mean square error，NRMSE)指标进行评定。

绝对平均误差为

(3)

归一化均方根误差为

(4)

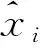
1.2 点预测模型

点预测模型结构如图2所示。将已修正的NWP风速结合NWP风向组成样本数据集，划分出训练样本和测试样本。预测模型输入量为归一化的NWP修正风速值、NWP风向正弦值和NWP风向余弦值，输出量为归一化的实际功率值，隐含层层数为单层。输入层神经元数目为3，输出层神经元数目为1，根据式(2)确定隐含层神经元个数。

构造好BP神经网络模型后进行训练，从而求得风电功率点预测值。预测结果精度同样采用NMAE和NRMSE指标进行评定。

2 风电功率概率区间预测

2.1 概率密度函数

非参数核密度估计(kernel density estimation，KDE)是一种无需事先假设分布，直接从数据本身得到分布特征的方法，其估计精度高，灵活性强，可应用于不同风电场。利用KDE求得的概率密度函数为

(5)

式中:N为样本数量；h为窗宽；K(u)为核函数，u=h-1(e-ei)；ei为功率预测误差的第i个样本值。核函数K(·)主要有高斯核、均匀核、三角核和Epanechnikov函数[13]。

窗宽h是影响KDE光滑度的主要参数，当h选择过大时，数据会过渡均值化，从而影响KDE无法很好地估计数据特征，当h选择过小时，随机性会增加，从而使估计密度函数出现不规则的形状。因此本文利用式(6)先确定一个合适的初值h，然后根据置信区间的结果进行调整。

(6)

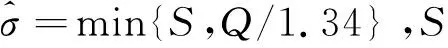
2.2 基于核密度估计的概率区间预测方法

基于前面的方法介绍，本文提出的基于非参数核密度估计的短期风电功率概率预测模型结构如图2所示。求取风电功率区间预测的步骤如图3所示。

①风电功率点预测。根据前文所述预测方法进行风电功率短期预测，得到点预测值。

②风电功率数据区段划分。根据功率大小进行区间划分。若某个功率区间段出现样本数据不足的情况，则将其与之相邻的功率区间进行整合。

③各区段相对误差统计。求出各区段风电功率预测值和实际值之间的相对误差e为

(7)

式中：Pt为风电功率实际值；Pp为风电功率预测值；Pmax为风电功率最大值。

④确定核函数K(·)和最优窗宽h的数值。

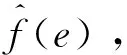
⑥计算预测区间。任意给定α(0<α<1)，在置信度1-α下，该预测区间以1-α的概率包含实际发电功率，则预测区间为

(8)

2.3 评价指标

概率预测的精度一般从可靠性和敏锐度两方面进行评估。可靠性选用预测区间覆盖率指标来评定，敏锐度选用预测区间宽度进行评定[4]。

预测区间覆盖率(prediction interval coverage probability，PICP)即表示预测区间对实际功率值的覆盖情况，覆盖率越高，证明包含实际风电功率值越多，其效果越好。区间覆盖率为

(9)

式中:N为预测样本数；Ki(a)为布尔量，若预测目标值落入预测区间值为1，否则为0[11,14]。

预测区间平均宽度(prediction interval normalized average width，PINAW)为

(10)

式中:Uxi为预测区间上限;Lxi为预测区间下限。

PICP 一定时，PINAW 越小表明区间范围越窄，预测精度越高。但PICP和PINAW这两个指标相互矛盾，两者在不能完全评价预测结果时，一般引入综合得分指标(Score)进行评估[4]。其计算方法如式(11)至式(13)所示。综合得分的绝对值越小，代表概率预测结果越好。Score值为

(11)

式中：

(12)

Ixi=Uxi-Lxi

(13)

3 实例分析

选用我国依兰风电场2012年1月1日至2月4日共35天的NWP数据和历史数据进行点预测与概率区间预测。数据采样频率为每15 min一次，一天(24 h)共有96个数据。

3.1 NWP风速的修正

选取1月3日、1月5日、1月18日、1月25日和2月2日，共5天的数据作为训练样本，未来29天数据作为预测样本，对未来29天的NWP风速进行修正。根据拟合修正原理，利用Matlab仿真平台，拟合出的修正风速曲线为

f(v)=1.119v+0.024 2

(14)

拟合修正法和BP神经网络修正法的具体NMAE和NRMSE评定结果如表1所示，修正风速对比如图4所示。从表1的评定结果和图4的风速对比可以看出，经过修正后的风速与实际风速更接近，两种修正方法的精度值相近。

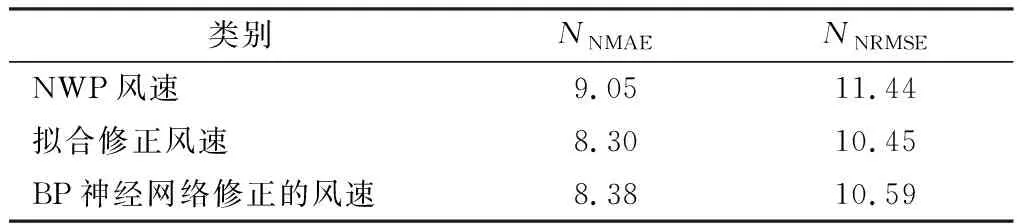
表1 风速修正评定结果 %

3.2 点预测

从29天预测样本的NWP风速、拟合修正风速和BP修正风速中选取最优风速值，结合NWP风向数据组成训练数据集，因此选取了1月10日、1月11日、1月14日、1月26日和2月4日数据作为训练样本，剩下的24天的数据为预测样本。将归一化的最优风速值、风向正弦、风向余弦作为BP神经网络的输入，实际风电功率作为模型期望输出，基于Matlab仿真软件，3种预测数据搭建的点预测模型结果如表2所示。从表2可以看出，利用修正风速样本建立的模型精度均高于原始的NWP风速样本，其中BP神经网络修正的风速样本精度最高，NMAE和NRMSE仅为15.35%和19.96%。

3.3 基于非参数核密度估计的概率区间预测

利用点预测模型，基于BP神经网络风速修正的功率测试样本进行概率预测。根据历史实际功率以及相应的预测功率，获取风电场预测误差的统计特征。1月12日、1月15日、1月17日、1月20日、1月24日、1月27日、1月30日和2月1日为训练日数据，对未来3天(72 h)的风电功率波动范围进行预测。对训练集划分功率区段，区间跨度为5 MW，共计8个区段。训练集各段内的预测误差点数如表3所示。

表2 功率预测评定结果 %

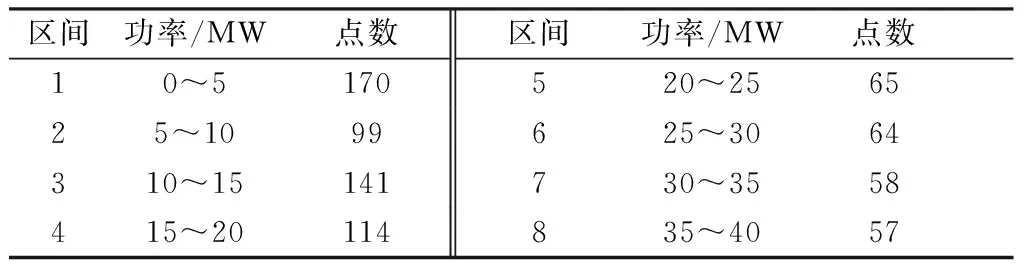
表3 各段内的预测误差点数

利用Matlab的Distribution Fitting 工具箱，对8个功率区间分别做参数法和非参数法的概率密度函数估计。图5是功率区间8的概率密度函数，对应的方法依次为：基于高斯函数、基于Logistic函数的参数法，以高斯函数、均匀函数、三角函数、Epanechnikov函数为核函数的非参数法。相应的分布函数如图6所示。

参数方法和非参数方法的具体预测结果如表4所示。其结果表明，选用4种核函数的非参数方法，效果均好于采用2种分布函数的参数方法。4种不同核函数的结果相近，差别很小。其中，以三角函数为核函数的核密度估计法的预测结果最好。在置信度为90%的情况下，PICP为98.61%，符合PICP数值应大于等于置信度的要求，PINAW为42.28%，符合在短期预测中数值应在30%～50%的要求。Score数值为-8.54%。具体区间概率预测如图7所示。

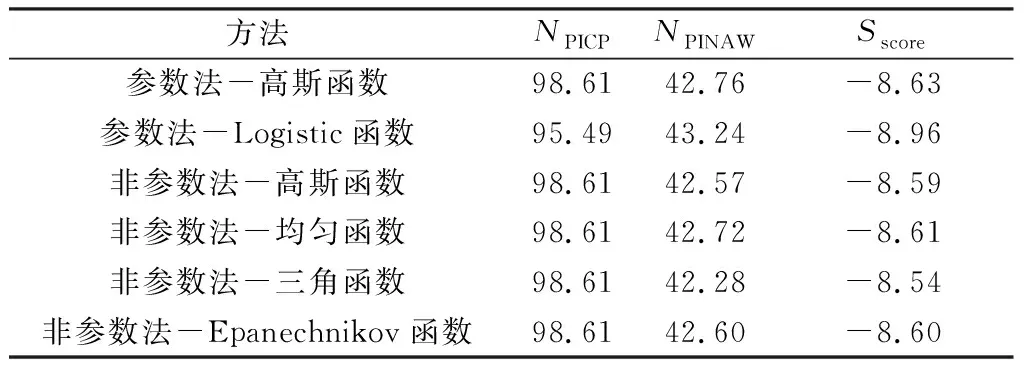
表4 置信度为90%的概率预测结果 %

4 结束语

为了能更全面地给电力调度部门提供发电依据，本文提出了一种基于点预测与非参数核密度估计的短期风电功率概率区间预测方法。与参数法概率区间预测方法相比，基于KDE的仿真结果更好，其中最好的是以三角函数为核函数的核密度估计法，在置信度为90%的情况下，该方法的PICP为98.61%，PINAW为42.28%，Score为-8.54%。说明本文提出的概率区间预测方法预测效果更准确，且在实际应用中可行。

本文的概率预测是基于点预测的结果构建的。考虑到点预测模型的精度会直接影响概率预测结果，今后将尝试省略掉点预测步骤，直接进行概率预测，以提高预测准确度。