考虑横向拉伸的压电材料层合板的自由振动研究
陈 静,郝育新
(北京信息科技大学 机电工程学院, 北京 100192)
0 引言
纤维增强复合材料具有强度高、刚度大、抗疲劳和耐腐蚀等优点,目前在航空航天、机械制造、汽车轮船和货车高铁等工程领域应用广泛,一直以来是国内外科研人员的关注热点。由于压电材料可以作为驱动器来控制复合材料薄壁结构的振动,含压电材料层的智能结构的动力学问题越来越受到人们的重视。Hyer等[1]基于Kirchhoff假设,研究了非对称正交铺设层合板的线性振动特性。Sharma等[2]利用里兹方法和样条函数技术研究了不同边界条件下反对称正交铺设层合板的自由振动。Abedi等[3]以多项式的形式展开为位移展开形式,研究了任意边界条件下复合材料层合板的自由振动。Tseng[4]等应用多维波数字滤波网络计算了正交对称铺设层合板的自由振动和弯曲。Fallah等[5]提出了一种新的无网格有限元法,用于预测复合材料层合板的频率。Quintana等[6]在里兹变分方法的基础上分析了对称铺设层合板的自由振动。Bouazza等[7]和Singh等[8]利用高阶剪切板理论研究了层合板的自由振动。Khandelwal等[9]考虑到层合板的界面问题,采用高阶zigzag理论对夹芯板和层合板的强迫振动和自由振动进行了分析。Zhao等[10]采用分段剪切变形理论,给出了层合板的振动特性。Ferreira等[11]利用Reissner混合变分定理研究了正交铺设层合板的弯曲和自由振动。
压电材料作为一种智能材料,可以用来控制与粘结或嵌入压电材料的复合层合结构的振动,因此越来越多地应用于形状控制、振动控制和健康监测等技术领域。目前常用的压电材料有压电陶瓷(PZT)和压电聚合物(PVDF)两种。由压电陶瓷纤维、电极层和外壳保护层组成的压电宏纤维复合材料(macro-fiber composite,MFC)是美国宇航局首次开发的,根据极化方向的不同可将其分为d31型和d33型两大类。在d31型MFC中,外加电场垂直于极化方向,而在MFC型d33中,外加电场与极化方向相互平行。由于具有较强的柔性、耐用性、易与层合薄壁结构集成等优点,MFC比单片压电陶瓷(PZT)具有更高的驱动性能,在智能执行器和传感器应用方面有广阔前景。
到目前为止,关于含MFC智能材料层的复合材料层合板固有振动影响的研究还很少。本文采用一种新的位移场,利用最小势能原理建立系统的动力学模型,利用瑞利-里兹法和切比雪夫多项式,得到了含有两种宏观纤维智能压电材料(MFC-d33和MFC-d31)的悬臂复合材料层合板的固有频率,研究粘贴有MFC智能层的悬臂正交铺设复合材料层合板的自由振动。
1 动力学方程
1.1 复合材料层合板和位移场
复合材料层合板的力学模型和坐标关系如图1所示,选取长为L、宽为b、厚度为h的复合材料层合板(0/90/90/0、0/0/90/90、90/0/0/90、0/90/0/90)和长为L1、宽为b1、厚度为h1的MFC层为研究对象,其中MFC层粘贴在悬臂板的上部,并在MFC层上施加不同的外部电压。
本文在Reddy高阶剪切变形位移场的基础上,考虑了横向拉伸的影响,所得位移场如下:
(1)
式中:u0(x,y,t)、v0(x,y,t)、w0(x,y,t)为参考中面上某点在3个方向上的位移分量;φx、φy分别表示该点绕y轴和x轴的旋转量;c1=(-4)/3h2;c2=f(h/2);f(z)=msec2(mz);m=1/5h。
复合材料层合板的应变与位移关系为:
(2)
1.2 复合材料层合板的本构关系
在新位移场的材料坐标系下,复合材料层合板第k层线性弹性本构关系为
(3)
由于复合材料层合板纤维铺层角度的存在,式(3)本构方程需要进行坐标变换,变换后的具体结果详见文献[12]。
压电材料MFC是将压电陶瓷纤维嵌入树脂并与组合电极复合在一起的夹层结构复合材料,包括MFC-d31和MFC-d33两种类型。其中MFC-31的极化方向沿厚度方向并垂直于压电纤维方向,MFC-d33型的极化方向与厚度方向垂直,平行于纤维方向。根据文献[13],可以得到d31型MFC层和d33型MFC层的本构方程,限于文章篇幅,在本文中不作详细展开。
1.3 能量关系表达式
复合材料层合板和MFC层的应变能分别为:
σxyεxy+σyzεyz+σxzεxz)dxdydz
(4a)
(4b)
复合材料层合板和MFC的动能分别为:
(5a)
(5b)
式中:ρ为复合材料层合板密度;ρe为MFC智能层的密度。
MFC层的电势能为
(6)
式中下标n为1时表示MFC-d33的x方向,n为3时表示MFC-d31的z方向。
系统的总势能和动能分别为:
U=Up+UMFC+Ue
(7a)
T=Tp+TMFC
(7b)
2 固有频率与振型求解
采用切比雪夫多项式和瑞利-里兹法求解含有智能压电层的复合材料层合板的自由振动。根据文献[14],系统的位移和转角假设为如下形式:
(8)
式中:ω为满足悬臂边界条件的频率;空间函数U0、V0、W0、Φx、Φy、W1可由切比雪夫多项式展开,详细推导过程见文献[14]。
根据瑞利-里兹法,可以得到含有MFC层的复合材料层合板的线性代数方程:
(9)
式(9)可以整理成以下形式:
(K-ω2M)P=0
(10)
式中:K为刚度矩阵;M为质量矩阵;P为待定参数向量。通过求解式(10),可以得到系统的振型和固有频率。
3 数值分析
3.1 方法可靠性与收敛性验证
为了验证本文理论和数值结果的准确性,采用本文中提出的方法所得到的简支边界条件下的矩形复合材料层合板的无量纲固有频率与三维弹性理论[15]和Reddy三阶剪切变形理论[16]给出的无量纲固有频率进行了对比分析,具体数值如表1和表2中所示,其中复合材料层合板参数为:a/h=5,μ12=μ13=μ23=0.25,E2=E3,G12=G13=0.6E2,G23=0.5E2,E1与E2的比值为任意值。从表1和表2中可以看出,采用本文提出的方法求解出的结果与文献数值结果较好地吻合,这说明本文提出的方法可以用来求解复合材料层合板自由振动的固有频率。
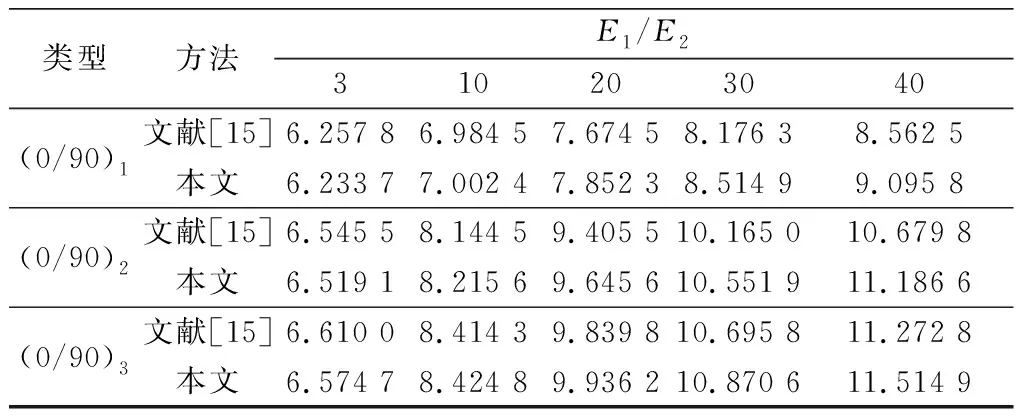
表1 两种方法下简支反对称层合板的无量纲基频比较值
表3是在简支边界条件下,容许函数分别取5×5、6×6、7×7时,求解出的 0/90 纤维铺层顺序的复合材料层合板前五阶固有频率,其中材料参数:μ12=μ13=μ23=0.25,E1=3 GPa,E2=E3=1 GPa,G12=G13=0.6E2,G23=0.5E2,从表中可以看出,当容许函数分别取5×5、6×6、7×7时,系统的前三阶固有频率相同,四阶、五阶固有频率略有不同,但差异较小。同时经过对比发现,在满足求解精度的情况下,再增加阶数,数值结果的精度虽然会更高,但是计算时间反而会增长。因此,经过综合考虑后,容许函数选择6×6进行下面的研究。

表2 两种方法下简支反对称正交铺设方形层合板的无量纲基频比较值
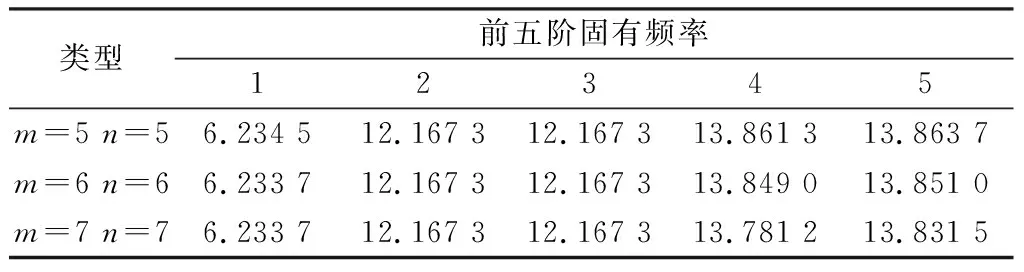
表3 (0/90)铺层方式下方形层合板前五阶无量纲频率的收敛性(a/h=5,E1/E2=3)
3.2 MFC的类型与通电电压对自由振动的影响
本文用于分析的MFC-d31(M8528-P3)、MFC-d33 (M8557-P1)和复合材料层合板的材料特性见参考文献[17]。其中MFC-d31施加电压的范围为0 V~+360 V(电极间距为0.18 mm),MFC-d33贴片的电压范围为-500 V~+1500 V(电极间距为0.5 mm)。MFC-d31、MFC-d33和复合材料层合板的尺寸分别为85 mm×57 mm×0.3 mm、85 mm×28 mm×0.3 mm和300 mm×75 mm×2 mm。MFC粘贴在复合材料层合板的上表面,与悬臂端保持一定距离,如图1所示。通过利用本文提出的方法,分别求出表面粘贴MFC-d31和MFC-d33两种类型的4种铺层方式(90/0/0/90,0/0/90/90,0/90/0/90,0/90/90/0)在不同电压下的复合材料层合板的固有频率,将所得到的数值结果进行研究分析,讨论MFC的类型不同和通电电压对系统自由振动的影响。
图2为计算得到的4种不同纤维铺层方式下复合材料层合板的前5种振型。从图中可以看出,对于90/0/0/90和0/0/90/90铺层方式下的复合材料层合板,弯曲振动发生在一阶、二阶和四阶,其余为扭转振动;对于0/90/0/90和0/90/90/0层合板,图2四层正交铺设复合材料层合板的振型通过数值计算可以得到上表面粘贴MFC-d31贴片的不同纤维铺层方式的复合材料层合板在多种外部电压作用下的最低弯曲和扭转频率参数,具体结果如图3所示。从图3中可以看出,在相同的外部电压作用下,不同的铺层方式的复合材料层合板的弯曲和扭转固有频率有较大的不同。这是由于纤维铺层方式和外部电压共同作用导致的。在某一外部电压作用下,纤维铺层方式对系统的影响是板的弯曲和扭转情况下固有频率的主导影响因素;在另一外部电压作用下,外部电压对系统的影响则为系统固有频率的主导影响因素。因此在MFC实际工程应用中,需要综合考虑铺层方式和外部电压对复合材料层合板振动特性的影响。此外通过观察发现,对于粘贴有MFC-d31型的复合材料层合板,增加电压有利于系统整体固有频率的增加,这是由于MFC-d31的压电应变常数d31和d32均为负,使得其刚度随外加电压的增大而增大,从而引起系统整体刚度的增加,因此结构整体的固有频率也会随着增加。
一阶、三阶和五阶为弯曲振动,其余为扭转振动。该研究结果表明,纤维铺层方式的不同对板的弯曲和扭转情况下的固有频率有较大的影响。这是因为纤维铺层方式不同,复合材料层合板的刚度会不同,所显现出来的振动形式也就会不同。
图4和图5为数值计算得到的外加电压为正电压和负电压两种情况下,粘贴MFC-d33型智能压电片的不同纤维铺层顺序的复合材料层合板最低弯曲和扭转频率的结果。通过将图4和图5中的数据结果与图3的数据结果进行比较,发现粘贴d33型MFC的复合材料层合板的频率更为复杂。其中,粘贴d33型MFC的层合板前两个弯曲频率随外加电压的增大而显著减小,另外两个低扭转频率随外加电压的增大而增大。这种现象出现的原因在于MFC-d31和MFC-d33的压电常数不同。与压电常数均为负的MFC-d31型相比,MFC-d33型的压电常数d33为正,而d32为负。在正向电压作用下,使得粘贴d33型MFC的层合板的x轴刚度减小,y轴刚度增大。因此,系统所有的弯曲频率下降,扭转频率增加,而当施加外部电压为负电压时,情况正好相反。
4 结束语
本文在Reddy三阶剪切变形理论的基础上,考虑横向拉伸的影响,利用瑞利—里兹法和切比雪夫多项式,求出含有两种类型压电宏观纤维智能材料层(MFC-d33和MFC-d31)的碳纤维增强复合材料层合悬臂板自由振动的固有频率和模态,并对比了MFC-d33和MFC-d31两种类型压电材料在通电情况下的驱动性能,讨论了粘贴不同类型的MFC与施加不同的外电压对复合材料层合板振动特性的影响。
结果表明,考虑横向拉伸影响的位移场理论可以用于复合材料层合板自由振动的研究;复合材料层合板的振动特性可以通过选择不同类型的MFC智能层与控制输入的电压来改变。此研究内容为进一步研究MFC 智能层对复合材料层合板振动特性的影响以及MFC未来在实际工程上的应用提供一定的理论参考。

