利用改进DBSCAN聚类实现多步式网络入侵类别检测
罗文华,许彩滇
(中国刑事警察学院 网络犯罪侦查系, 沈阳 110035)E-mail:luowenhua770404@126.com
1 引 言
随着存储空间及计算能力的迅速进步,对搜集、存储、管理及处理数据的能力大幅度提升,在网络入侵检测中应用机器学习技术,已成为近年来安全领域的研究热点[1].常用于网络入侵检测的算法有Kmeans、DBSCAN、PCA、K-NN、SVM、贝叶斯分类等算法.但这些算法的检测率较低或者误检率高,通过进一步改进提高了检测能力[2].Wei-Chao Lin等[3]将Kmeans算法和Knn算法结合使用后形成新的入侵检测算法CANN,并基于KDDCUP 99数据集对该算法进行了较有效的验证.戴敏[4]构建一种并行化的量子粒子群优化(QPSO)算法,对KDDCUP 99数据集进行特征选择,实现一种并行化的朴素贝叶斯分类器用于网络入侵检测.郭慧等[5]通过云模型对KDDCUP 99数据集连续属性进行离散化,引入加权选择概率函数,使得决策树算法能检测出全部类别攻击.然而,上述网络入侵检测算法多为单步式检测的形式,具有一定的缺点.
单步式网络入侵检测算法在检测非平衡(各类数据分布严重不均)数据集时,往往难以准确高效地检测所有类别的数据.例如,对于罕见攻击U2R类数据,由于其占比很低,被检测的成功率往往不高[6].Solane Duque等[7]利用基于签名的K-means算法构建一个自动识别数据类群的入侵检测算法,一次性对NSL-KDD数据集划分,虽降低了误报率,但整体类别的数据的检测率较低.相比单步式检测,多步式检测通过逐步划分减少数据量的方式将非平衡数据往均衡状态方向发展,提升罕见入侵行为数据的被检测率.不仅能适应平衡数据集,也能良好地适应非平衡据集,具有更强的应用性.因此,考虑将基于聚类算法的多步检测思路应用到网络入侵类别检测中.
K-means算法作为一种常用的入侵检测聚类算法,其应用广泛、实现简单.但是,K-means聚类算法的初始聚类中心是随机选取的,聚类中心数需要人为设定,导致聚类结果不稳定[8];并且K-means聚类算法基于距离划分数据,结果簇趋向于球形[9],对非球形分布数据的适用性较差.DBSCAN聚类算法则是一种基于密度划分数据的方法,不需要事先设定聚类中心的数量[10].由于基于密度划分,DBSCAN算法能够根据数据在空间分布的密度情况自行划分簇数,而且数据密度分布是稳定的,使得聚类结果具有稳定性.但是,DBSCAN算法需要人为设定最小包含点数(MinPts)和扫描半径(Eps)参数,依赖多次经验才能合理地选择参数,否则难有准确的聚类结果.为使入侵检测输出准确稳定的聚类结果,提升检测方法对球形与非球形数据的适用性,提出一种基于密度自适应计算参数的改进DBSCAN聚类算法.
基于多步检测思路及改进DBSCAN聚类算法,提出一种基于改进DBSCAN聚类的多步式网络入侵类别检测算法.该算法可以实现网络行为数据的自动聚类以及优化,并对于如何依据数据自身分布确定DBSCAN聚类参数进行了深入研究.本文按如下结构进行组织,除“引言”部分外,第2节着重于描述NSL-KDD数据集以及对其数据的特征处理过程;第3节重点基于入侵检测视角说明如何对DBSCAN聚类算法进行改进,阐述自适应计算聚类参数的方法与依据;第4节说明基于改进DBSCAN聚类的多步式网络入侵类别检测过程;第5节展示入侵检测效果,并与其他入侵检测方法进行比较说明;第6节对本文的主要工作进行总结,指出了不足并说明未来研究的方向.
2 数据集确定及特征处理
NSL-KDD训练集[11]有125973条数据,测试集有22544条数据.这些数据有42维,其中前41维为特征值,第42维为属性标识.NSL-KDD数据集包含Normal、Dos、Probe、U2R和R2L五大类行为数据,且各类数据的占比类似于现实中各类行为出现的频率,故NSL-KDD数据集适合作为入侵类别检测算法的验证数据集.随着NSL-KDD数据集越来越广泛应用于网络入侵检测领域,NSL-KDD数据集验证网络入侵检测算法的有效性得到普遍认同,具有权威代表性.
NSL-KDD数据集可以通过提取代表性维度进行降维,提高效率并找出有用的特征子集.Sang-Hyun Choi和Hee-Su Chae[12]基于NSL-KDD数据集将一种有效的分类决策树算法应用于评估维度约简方法选取代表性维度.刘白璐、杨雅等[13]以遗传算法和SOM神经网络作为评价模型,将39维早期特征减少为29维.ZHANG Xue-qin等[14]利用Fisher评分方法对每个维度进行评分,依据维度评分的大小选取具有代表性维度.相对于分类决策树约简维度的方法,以及基于神经网络选择特征的方法,以Fisher评分作为维度评分方法,能够在不同划分情形下自动判断出代表性维度,达到数据降维的目的,实现在低维度空间按照划分顺序划分数据.同时,代表性维度可以按其Fisher评分在所有维度评分总分的占比,重新被赋予权重,使各维度在检测过程中的权重符合其划分能力.
2.1 转化文字型特征值
NSL-KDD数据集中Protocol_type(2)、Service(3)、Flag(4)维度的特征值为文字型,如Tcp、ftp_data和SF,无法直接参与到Fisher评分和聚类中的样本间距离计算.若直接排除这3个维度的特征值,可能影响到维度评分和聚类的结果.因此,保留这3个维度的特征值,并用文字型特征值在数据集中出现的次数替换对应的数值型特征值.在同一维度中,文字型特征值替换它们自身出现的次数后,能够反映出与其他特征值的差异.转化后,Protocol_type(2)、Service(3)、Flag(4)维度的特征值与其他维度的特征值共同参与维度评分和聚类.
2.2 基于改进Fisher评分进行维度评分
NSL-KDD数据集的每一个样本是41维的特征向量及属性标识,在入侵检测需要进行降维操作,以此减少大数据量聚类需要的算力要求,实现高效准确的入侵检测.在多维度中选取一部分具有代表性的特征维度,是一种常见有效的降维方法.Fisher评分具体实施时,在多维度中挑选一个维度的特征向量作为分类依据,利用SVM向量机分类出训练集中的正常簇和异常簇,然后计算此维度的特征向量对应的Fisher评分,循环上述过程,直到多个维度的Fisher评分计算完成.在分类正常簇和Dos簇、正常簇和Probe簇、正常簇和U2R簇、正常簇和R2L簇时,也可以使用上述Fisher评分方法.Fisher评分的定义为:
(1)
其中,Sb为两个簇间的距离,Sw为簇内距离.
(2)

(3)
(4)
(5)
其中,x∈+1和x∈-1的+1、-1分别表示正常簇、异常簇,x表示节点特征值.而Sw的定义为:
Sw=S1+S2
(6)
(7)
(8)
其中,N1是正常簇中的节点数,N2是异常簇中的节点数;σ1、σ2分别为正常簇、异常簇内距离方差.
但是,上述方法中基于SVM向量机进行分类具有一定的缺陷.由于SVM向量机很难确保核函数完全让数据集线性可分,这导致分离面难以准确介于两个不同类之间.所以,为缓解这个问题,SVM向量机允许分离面处于软间隔状态,一些介于ε间隔带(位于分离面两侧,宽度为ε)样本会被分错.
针对此缺陷,结合SVM向量机和KNN算法的SVM-KNN算法[15],能对处于ε间隔带的样本进一步确定属性.首先用SVM向量机分类数据集,然后基于KNN算法对落入ε间隔带的样本点重新分类,改善分类效果.将Fisher评分方法中的SVM向量机改进为SVM-KNN分类算法,提升评分的准确度.
2.3 代表性维度按比例赋予权重
由于每个维度的特征值的最大值不同,在用多维度数据计算样本点间距离时,特征值总体偏大的维度数据对计算结果影响更大,而特征值总体偏小的维度对计算结果影响会变小,造成维度间的地位偏离Fisher评分结果.例如:计算样本点1(100,0.01)与样本点2(50,1)间的距离,其中维度2的Fisher评分高于维度1.可知,这种情况下,即使维度2比维度1更具有划分能力(Fisher评分),但由于维度1的特征值总体上大于维度2,造成距离的计算结果绝大程度上受维度1影响.
因此,在数据预处理阶段增加维度按比例加减权这一步骤.让具有代表性的维度按照各自Fisher评分占总分的比例,对其赋予相应的权重.维度按比例赋予权重的过程如下:
(9)
说明:xi为某维度中的特征值,xmax为维度中最大的特征值,Fi为维度i的Fisher评分,Fsum为各维度的Fisher评分之和,100为总权重,Xi为xi更新后的值.
3 DBSCAN聚类算法的改进
通过改进DBSCAN聚类算法,实现其能够自动且较准确地划分网络行为数据.在改进DBSCAN聚类应用于多步式网络入侵类别检测时,该聚类算法能自动且较准确地划分出不同网络入侵类别的数据,实现较好的检测效果.
3.1 改进基本思路
由于数据在多维空间中的分布体现出相似性和相异性,相似的数据相互靠得近,而相异的数据互相离得远.所以,相似数据所在的区域呈现凝聚态,样本点的分布密度较高,而相异数据间的区域为簇间分隔区域,样本点分布密度较低.在高密度数据集合之间存在着低密度区域,且低密度区域存在着一定的宽度.所以,在样本点密度参数不低于临界点(其恰好能分辨出两个簇间的空间,指明这个空间是簇间分隔区域)的情况下,随着密度参数的逐渐降低,聚类结果的簇数会呈现收敛状态,并在一定密度值区间内保持稳定.同时,密度值越小,则噪声率越低,而且聚类结果越准确[16].这是因为随着密度参数的降低,越多的低密度样本点被划分进簇,因此噪声率变低.综上所述,在一定密度值区间内,密度参数越小,则聚类效果越好.因此,临界点密度是最理想的DBSCAN算法参数,其对应的样本点数及拐点半径即为最小包含点数(MinPts)和扫描半径(Eps)参数.
3.2 聚类参数的计算
基于最小二乘法曲线拟合和样本点密度分布情况,自适应计算聚类参数.实验发现用曲线拟合计算拐点半径的思路计算每个点到其他点的距离后,统计距离与样本点数的关系,可以发现在某个距离区间内存在密集的点,这个密集的区域到中心点的半径可作为DBSCAN聚类的扫描半径(Eps),即拐点半径ri.
拐点半径ri计算方法为:首先计算样本点xi与其他样本点xj的欧氏距离dij,将距离集{j=1,…,n(j≠i)|dij}从大到小排序,得到新的距离集{1≤m≤(n-1)|dm};然后以距离集{1≤m≤(n-1)|dm}作“m-dm”曲线图(横坐标为dm对应的序号m,纵坐标为距离dm);最后基于最小二乘法曲线拟合原理,利用三次方程拟合“m-dm”二维曲线;并利用二阶求导计算出曲线拐点对应的纵坐标y值,y即为拐点半径ri,如图1.

图1 基于距离集计算拐点半径
通过三次方程曲线拟合和二阶求导,可大致计算出这个半径ri和在此区域内的样本点数ni.遍历数据集,计算每个点对应的拐点半径ri,及以ri为半径的空间区域内的样本点数ni,并求出相应的样本点密度,形成密度集densitydata.
在选择最小包含点数(MinPts)和扫描半径(Eps)参数时,由于这两个参数在聚类中全局使用,所以它们应该尽可能多地区分出簇间分隔区域.密度集densitydata有每个点对应的点分布密度,将其按大小顺序排列,绘制分布曲线,呈现出一段密度曲线平缓稳定的区间range,见图2.当聚类参数的密度在区间range左边时,密度对应的参数值低于大部分样本点周围的密度,容易将簇间分隔区域错误识别为簇内区域;当聚类参数的密度在区间range右边时,密度对应的参数值高于大部分样本点周围的密度,容易将簇内区域错误识别为簇间分隔区域.密度区间range中的最小密度值最接近于临界点密度,其对应的拐点半径ri及样本点数ni作为DBSCAN聚类算法的MinPts 和 Eps 参数.
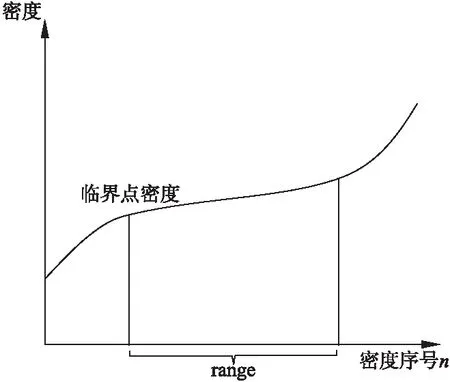
图2 密度曲线的稳定区间range
3.3 具体聚类步骤
Step 1.计算样本点xi与其他样本点xj的欧氏距离,距离集{j=1,…,n(j≠i)|dij}从大到小排序,得到新的距离集{1≤m≤(n-1)|dm};
Step 2.用新的距离集{1≤m≤(n-1)|dm}基于最小二乘法曲线拟合,产生三次方程,通过对此三次方程二阶求导计算样本点xi的拐点半径ri及样本点数ni,然后计算样本点对应的密度ρ;
Step 3.循环Step 1-Step 2,遍历数据集的每一个样本点,计算出每个样本点对应的密度ρ,形成密度集densitydata;
Step 4.密度集densitydata有每个样本点的密度ρ,将其按大小顺序排列,基于最小二乘法曲线拟合,产生三次方程,通过对此三次方程一阶求导计算出曲线的凸点D;
Step 5.用凸点D对应的半径和样本点数作为DBSCAN聚类中的MinPts 和 Eps 参数;
Step 6.检查数据集中尚未检查过的样本点xi,如果其未被处理(即被标为噪声点或被划分到某个簇),则检查其邻域(扫描半径Eps内的区域),若包含的对象数大于或等于最小包含点数MinPts,则建立新的簇Ci,将其中所有的样本点xi划分到候选集N,否则将xi标记为噪点;
Step 7.对候选集N中所有尚未被处理的样本点xi,检查样本点xi的邻域,若至少包含MinPts个样本点,则将这些样本加入候选集N中;
Step 8.如果样本点xi未归入任何一个簇,则将样本点xi划分到Ci中;
Step 9.重复Step 7-Step 8,继续检查候选集N中未处理的对象,直到候选集N为空集;
Step 10.重复Step 6-Step 9,直到全部样本都被划分到某个簇中或被标为噪声.
4 多步式网络入侵类别检测
4.1 基于Fisher评分确定多步检测顺序
采用多步检测的目的是通过对网络行为数据集的逐步划分减少大类数据量,将非平衡数据往均衡状态方向发展,并且既要保证大类网络行为数据的检测率,又要提升罕见入侵行为数据的检测率.由于多步检测顺序要能够整体上准确划分好各类数据,故每一步划分情形的特征维度划分效果影响着整体的检测结果.多步检测顺序的确定,应以网络行为数据集的具体特征为基础,评价特征维度在不同划分顺序的每一步划分情形下的价值,并以此价值的总和为考量确定多步检测顺序.改进的Fisher评分是一种评价特征维度价值的方法,可应用于多步检测顺序的确定
不同的划分顺序,其Fisher评分的总体分数不同.由于维度的Fisher评分越大,其在划分数据时的效果越好.因此,为了提高聚类算法的划分效果,应该选择总体上Fisher评分较高的划分顺序.
选用顺序1和顺序2[17]进行比较,顺序1为实验假设,结果如表1所示.

表1 不同划分顺序的Fisher评分情况
由表1可知,划分顺序2的总体Fisher评分更高,故入侵类别检测的多步顺序为:
Step 1.将NSL-KDD数据集划分为2类,大类为Normal、U2R、R2L类,小类为Dos、Probe类;
Step 2.将Step 1中的Dos、Probe类划分为2类,大类为Dos类,小类为Probe类;
Step 3.将Step 1中的Normal、U2R、R2L类划分为2类,大类为Normal、U2R类,小类为R2L类;
Step 4.将Step 3中的Normal、U2R类划分为2类,大类为Normal类,小类为U2R类.
4.2 多步式网络入侵类别检测流程
在确定多步检测顺序后,结合数据特征处理,基于改进DBSCAN聚类算法进行多步式网络入侵类别检测,具体流程见图3.

图3 检测流程
图3中,1) 转化文字型特征值:以各特征值的出现频次替代 NSL-KDD数据的Protocol_type、Service、Flag维度的文字型特征值;2) 各维度重新分配权重:数据降维后,参与下一步聚类的维度按各自Fisher评分在总分的占比,重新被分配权重;3) Dos、Probe、Normal、U2R和R2L表示不同类别的网络行为数据集群;4) 检测结果:收集划分好的各类网络行为数据,并标识及输出.
5 实验结果分析
实验平台为64位的Windows 10系统,内存为8GB,CPU为英特尔酷睿i7-7700HQ.算法实现的过程使用编程语言Python 3.7.实验过程见图4.

图4 检测的实验过程
实验中,训练集的作用仅为Fisher评分,而数据降维及其后面的各阶段只有测试集参与.
多步聚类按第3节确定的顺序进行.在每一步聚类前,依据具体的划分情形选取Fisher评分结果,然后对测试集进行数据降维,以及将代表性维度按比例赋予权重.更新后的测试集被输入到聚类算法中,基于自适应设参的DBSCAN聚类算法对其进行划分.
5.1 评估指标
将聚类的数据集按其真实类别与聚类算法预测类别的组合分为真正例(TP)、假正例(FP)、真反例(TN)、假反例(FN),它们存在关系:TP+FP+TN+FN=数据集样本数.
真正例(TP):预测类别为正例,且真实类别也为正例的数据.
假正例(FP):预测类别为正例,但真实类别为反例的数据.
真反例(TN):预测类别为反例,且真实类别也为反例的数据.
假反例(FN):预测类别为反例,但真实类别为正例的数据.
准确度:正确检测出的正例和反例样本数除以测试集的全部样本个数的百分比RI.
(10)
查准率:测试集中正例(或反例)的样本被检测为正例(或反例)的样本数TP(TN)除以检测出的正例(或反例)样本数的百分比P.

(11)
查全率:测试集中正例(或反例)的样本被检测为正例(或反例)的样本数TP(TN)除以真实的正例(或反例)样本数的百分比R.

(12)
误检率:测试集中正例(或反例)的样本被检测为反例(或正例)样本的个数FN(FP)除以测试集中所有正常样本个数的百分比f.
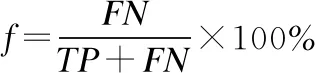
(13)
5.2 Fisher评分筛选的代表性维度
多步聚类中,每一步聚类对应一种划分情形,并依据表2中对应划分情形的代表性维度进行聚类.

表2 各划分情形的代表性维度
5.3 聚类结果及分析
从表3可以看出,多步聚类过程中,自适应设参的改进DBSCAN聚类算法保持稳定的聚类簇数,达到每一步聚类的划分目的.由于样本数据划分依据二分类的高Fisher评分维度,聚类中的样本数据在空间呈现类二分态.改进的DBSCAN算法基于空间密度分布,判断出样本数据的类二分态分布,进而自适应设定出较准确的聚类参数,使得聚类簇数基本满足划分需求.虽然Step 2中的簇数为3,但大簇是Dos类,两小簇主要是Probe类.同时,由于最小包含点数(MinPts)和扫描半径(Eps)参数得到较准确的设置,改进的DBSCAN算法稳定保持低的噪声率和较高的准确度,表现出良好的聚类性能.

表3 聚类算法的性能
表4是统计混淆矩阵,显示测试集在分布聚类后的详细检测结果.表中样本数总和为22435,不计入噪点数109,故与测试集样本总数22544不同.由表4可知,U2R被误检为Normal的情况较多,且在划分后的U2R中,非U2R样本的Normal占比高.由于U2R与Normal类样本的特征值较相似,导致在空间分布中较接近,提高了准确检测的难度.

表4 聚类的划分结果
由表5数据可知,聚类结果中各类数据的查准率和查全率较均衡地处于90%左右,划分效果较为均衡,保证检测各类数据的较好性能,这是多步聚类相较于单步聚类(或分类)的优点.同时,划分5个类别数据的误检率较低,其中的Normal类最低,说明算法能较好地避免正常网络行为被误判.

表5 聚类结果整体度量
从表6可知,对于检测罕见攻击U2R类,多步检测方法的查准率和查全率均比单步检测方法高,检测结果的更准确.而单步检测方法的检测效果较一般,这是单步检测的普遍现象.由于训练集和测试集中U2R的样本量少,且U2R样本和Normal样本在空间分布上较接近,单步检测很难做到既检测好Normal、Dos、PROB、R2L类,又检测好U2R类.而在多步检测中,可以通过先检测出其他类的数据样本,进而提高U2R类在待检数据中的比例;还能在个别步骤中仅选取能够良好划分U2R类和Normal类的维度,使两者在聚类空间中尽量分离.因此,多步检测的检测效果更好.

表6 检测NSL-KDD数据集中U2R类的效果比较
6 结 语
在不同的网络行为数据集中,多步检测顺序的确定,以整体检测效果好坏作为判断标准.其中,整体检测效果的评价需要可量化的计算方法.改进Fisher评分是一种可量化的计算方法,其对维度评分的大小等于维度划分能力的大小,而维度划分能力的大小与检测效果成正比.通过计算并统计不同划分顺序的维度划分能力总分,即可以总分高的划分顺序作为多步检测顺序.因此,基于改进Fisher评分确定多步检测顺序的方法,在不同的网络行为数据集中都能被应用.
在改进Fisher评分自动确定代表性特征和确定多步聚类检测顺序的基础上,将基于最小二乘法拟合原理和曲线拟合的拐点半径计算,应用于DBSCAN聚类中感知判断网络行为数据的空间分布态,以判断结果实现自适应设置聚类参数,实现网络行为数据的自动合理地聚类,提高入侵类别检测算法的自动化程度和智能性.同时,该检测算法较有效地解决非平衡网络行为数据中全类别检验难的问题.该检测算法能在保证良好检测效果的情况下,适应复杂的网络行为数据变化,减少算法使用难度,具有较高的应用价值.
在维度的Fisher评分实验中,仅对两种划分顺序进行比较,未能够明确得出最合理的划分顺序.同时,在改进DBSCAN聚类算法的自适应设参阶段中,数据量越大,曲线拟合的时间越长,影响检测速度.因此,如何判断最合理的划分顺序以及提升曲线拟合效率是下一步研究的重点方向.

