面向机载光电平台的串联球面机构运动学建模与验模

王玫羽,田大鹏*，郭立红

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049；3.中国科学院 航空光学成像与测量重点实验室，吉林 长春 130033)

1 引 言

机载光电平台是一种光机电一体化设备，由机械伺服框架内承载光学成像系统，适用于侦察、搜救、定位等多种军民应用。随着使用需求的发展，机载光电平台内需要集成更多高性能的光电传感器。减小光电平台自身的体积、质量，增加光电平台内部可安装载荷的空间以提高载荷比对提升机载光电平台的功能和性能都有重要的意义[1]。

传统的机载光电平台以二轴二框架、三轴三框架、二轴四框架这三种结构为主[2]。二轴二框架平台是一种最为成熟的平台结构，它对于小负载、高动态的应用十分有效；缺点是大角度失稳无法实现垂直对地跟踪，过顶时导致图像产生像旋。三轴三框架和二轴四框架光电平台解决了二轴二框架的结构问题，但平台自身体积、质量较大，负载装配空间有限[3]。传统的框架结构将轴系组件安装在一个球体内部，占据了球体内可用于安装光电载荷的空间，限制了光电平台载荷比的提高。

采用串联球面机构可解决这一问题。球面机构是一种介于平面机构和空间机构之间的特殊机构，转动副的轴线交于空间内一点，并且转动副均在同心球面上运动[4]。通过将轴系组件布置在球面上，可以在球形空间内排布更多的光电载荷。目前，对于空间球面机构的研究主要集中于多支链的并联球面机构。但并联机构自身的耦合特性限制了球面并联机构的控制精度[5-6]。空间开链串联球面机构结构简单、不易发生干涉、便于控制。现阶段针对空间开链球面机构的研究结果较少，主要集中于微创手术器械方面的应用[7-8]。实际上，得益于三轴轴线非垂直相交的特殊关节位置关系，利用该机构构建的非封闭负载空间也能够提升光电平台的载荷比。三自由度串联球面机构机载光电平台较传统框架结构更容易实现对小角度、高精度光电平台的精确控制。

该机构的应用前提是其运动学模型的建立。文献[9]提出了只有转动副，且转动副轴线交于空间内一点的3-3R三自由度球面并联机构，并逐渐发展出该机构的多种变型。文献[10]中提出了基于3-3R机构的转动副轴线共面的球面机构。文献[11]提出了一种基于三自由度并联机构的太阳追踪装置，并对机构进行了运动学分析与仿真验证。文献[12]介绍了一种远中心运动的球面机构，能够避免机构工作过程中与环境中物体的碰撞，文中分析了该机构的运动学和工作空间。随着球面并联机构研究的深入，混联球面机构的应用也得到了发展，文献[13-14]介绍了一种灵活度高，结构紧凑的混联球面机构，通过对静力学和弹性力分析，验证了机构的可靠性，并对机构的工作空间进行了讨论。文献[15]阐述了球面混合机构手术机械的运动学、动力学以及控制策略。在串联球面机构方面，文献[7-8]设计了手术机器人串联开链球面机构，并对球面机构进行了运动学、灵敏度与工作空间分析，由于其机构设计具有特殊性，并非面向机载光电平台，无法直接应用。Lewis等针对光电平台负载框内部空间有限、不能很好地适应各种光电载荷安装的弊端，提出了一种质量轻、体积小、载荷比大的光电平台内框架结构。采用三个三轴万向节连接负载和基座并采用与串联球面机构相似的轴系布置[16]。文献[17]对采用三轴万向节的光电平台正运动学进行了研究，但缺少逆运动学且未对模型进行验证。文献[18]设计了一种基于球面机构的光电平台内框架，降低了框架的体积质量，提高了带负载能力，但缺少运动学模型。

机载光电平台的串联球面机构要实现实际工程应用必须首先获得精确、易于解算的运动学模型。然而，现有的研究中仍然缺少能够满足机载光电平台实际应用的完整、准确的运动学模型，限制了机构的实际应用。本文基于机器人领域的D-H参数法建立了一种串联球面机构正、逆运动学模型；通过多体动力学软件联合仿真以及实际实验对模型进行了验证，为后续开展实际应用奠定了基础。

2 串联球面机构的建模

本文首先建立了一种面向机载光电平台的串联球面机构的坐标系，在此基础上基于机器人机构学领域的D-H参数法进行了正、逆运动学建模。

2.1 串联球面机构的坐标系建立

如图1所示，串联球面机构光电平台采用斜交关节机构，通过三个转动副连接光电平台基座与负载。不同于正交机构转动副两两垂直的结构特性，该机构采用转动关节相互斜交的紧凑结构，三个转动副轴线延长线于空间内交于一点O，转动副A，B，C在以O为球心的球面上运动，即可实现光电平台负载横滚、俯仰和方位的运动。

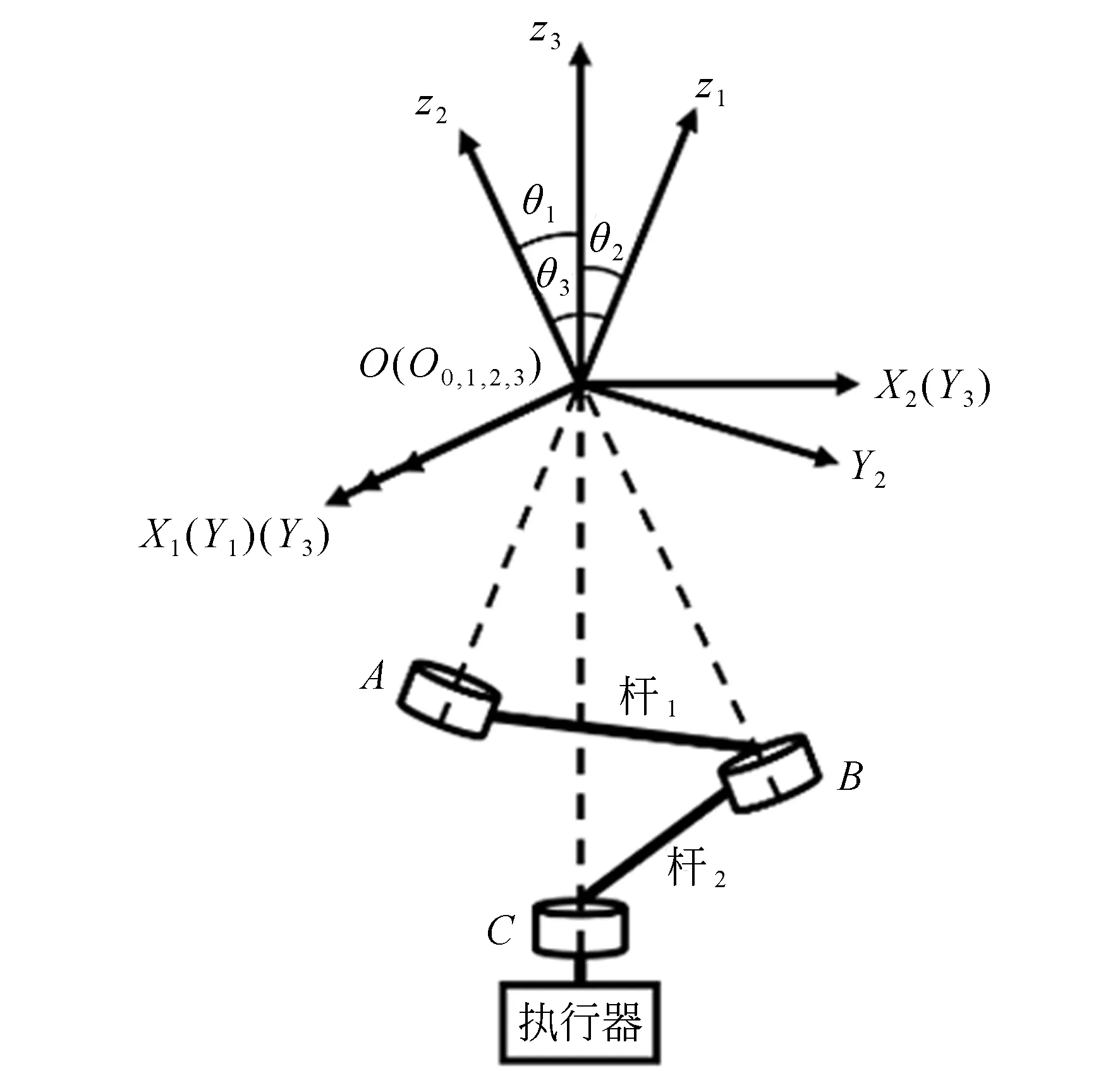
图1 串联球面机构坐标系示意图Fig.1 Coordinate system diagram of series spherical mechanism

本文基于机器人领域的D-H参数法建立串联球面机构坐标系[19]。选取串联球面机构转动副的轴线方向为坐标系的z轴方向，机构连杆与转动副轴线所在平面的公垂线方向为x轴所在方向，y轴方向由右手定则确定。据此建立串联球面机构坐标系，如图1所示。图中，O-XYZ为全局坐标系；O0-XYZ为光电平台的基座局部坐标系，与全局坐标系重合；O1,2,3-XYZ为转动副A，B，C的局部坐标系；θi为zi-1轴与zi轴所成夹角，即转动副轴线夹角；βi+1为yi轴与yi+1轴所成夹角，本文中βi+1=0；αi+1为xi轴与xi+1轴所成夹角，即驱动副的转动角度。

由于串联球面机构采用三轴相交结构，在使用D-H参数法建立运动学模型时，可以省去位置信息参数，将典型的4×4位姿D-H矩阵简化为3×3的姿态矩阵。根据D-H参数法可建立D-H参数，如表1所示。

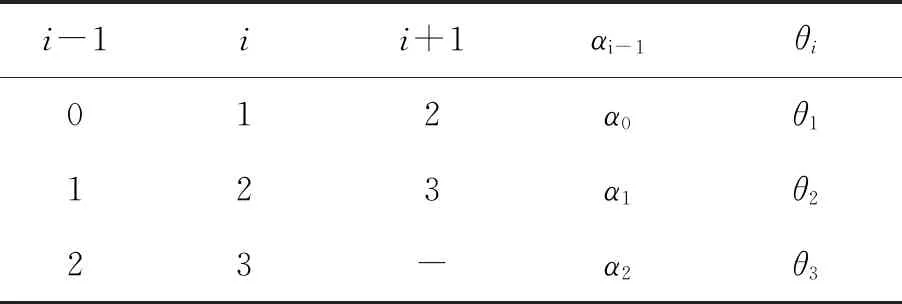
表1 D-H参数表

2.2 串联球面机构的运动学建模

串联球面机构的运动学正解是在已知三个驱动副输入角度(α0,α1,α2)的前提下，利用坐标系变换关系，求解光电平台负载姿态角度(R,P,Y)的过程。其中，R为负载滚转角；P为负载俯仰角；Y为负载方位角。

参照表1，机构参数(αi-1,θi)表示光电平台负载在运动学坐标系i中的位姿，依据D-H参数法，定义广义旋转矩阵为：

(1)

其中：

t11=cosαi-1cosβi-1，

t12=-sinαi-1cosβi-1，

t13=sinβi-1，

t21=cosθisinαi-1+cosαi-1sinβi-1sinθi，

t22=cosθicosαi-1-sinαi-1sinβi-1sinθi，

t23=-cosβi-1sinθi，

t31=sinαi-1sinθi-cosαi-1sinβi-1cosθi，

t32=sinθicosαi-1+sinαi-1sinβi-1cosθi，

t33=cosβi-1cosθi.

故由负载坐标系O3-XYZ至全局坐标系O-XYZ的旋转矩阵为：

(2)

(3)

运动学逆解是指已知末端负载在全局坐标系O-XYZ中的位姿(R,P,Y)，通过逆运动学求解负载在运动学坐标系i中的位姿参数(αi-1,θi)，使负载实现该位姿。光电平台负载位姿通常采用惯性测量元件获取。依据D-H参数法和惯性测量元件特性，定义广义旋转矩阵为：

(4)

其中：

q11=cosαi-1cosβi-1，

q12=-cosθisinαi-1+cosαi-1sinβi-1sinθi，

q13=sinαi-1sinθi+cosαi-1sinβi-1cosθi，

q21=sinαi-1cosβi-1，

q22=cosθicosαi-1+sinαi-1sinβi-1sinθi，

q23=-sinθicosαi-1+sinαi-1sinβi-1cosθi，

q31=-sinβi-1，

q32=cosβi-1sinθi，

q33=cosβi-1cosθi.

tij=qij,(i=1,2,3;j=1,2,3).

(5)

求解方程(5)，可得关节角α0,α1,α2，即逆运动学模型：

(6)

其中：

a3=sinα1sinθ2，

b3=cosα1sinθ2cosθ3+sinθ3cosθ2，

c3=q31cosθ2-q21sinθ2，

a1=q11，

b1=q21cosθ2+q31sinθ2，

c1=cosα1cosα2-sinα1cosθ3sinα2，

3 基于ADAMS的仿真验证

利用多体动力学分析软件与MATLAB联合仿真，比对软件求解和模型解析出的结果之间的差异对模型进行验证。

使用ADAMS/View虚拟样机开发系统软件互式图形环境和零件库、约束库、力库，创建串联球面机构完全参数化的机械系统几何模型，将模型导入MATLAB软件中进行联合仿真，见图2。

给定串联球面机构光电平台的驱动副一组幅值为6°，周期为0.4 s的正弦输入信号，得到负载的姿态变化曲线如图3所示。

图3 负载姿态角度的变化曲线Fig.3 Attitude angle change curves of load camera

ADAMS几何模型负载姿态位置与运动学建模的误差如图4所示。经验证，串联球面机构正运动学模型正确。

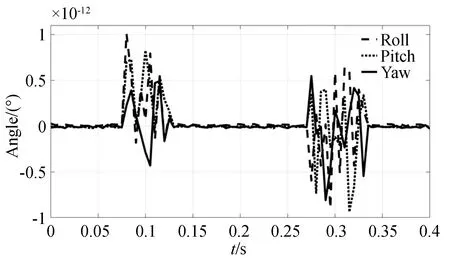
图4 姿态角输出误差Fig.4 Output error of attitude angles

在MATLAB中搭建串联球面机构光电平台逆运动学系统仿真框图，如图5所示。

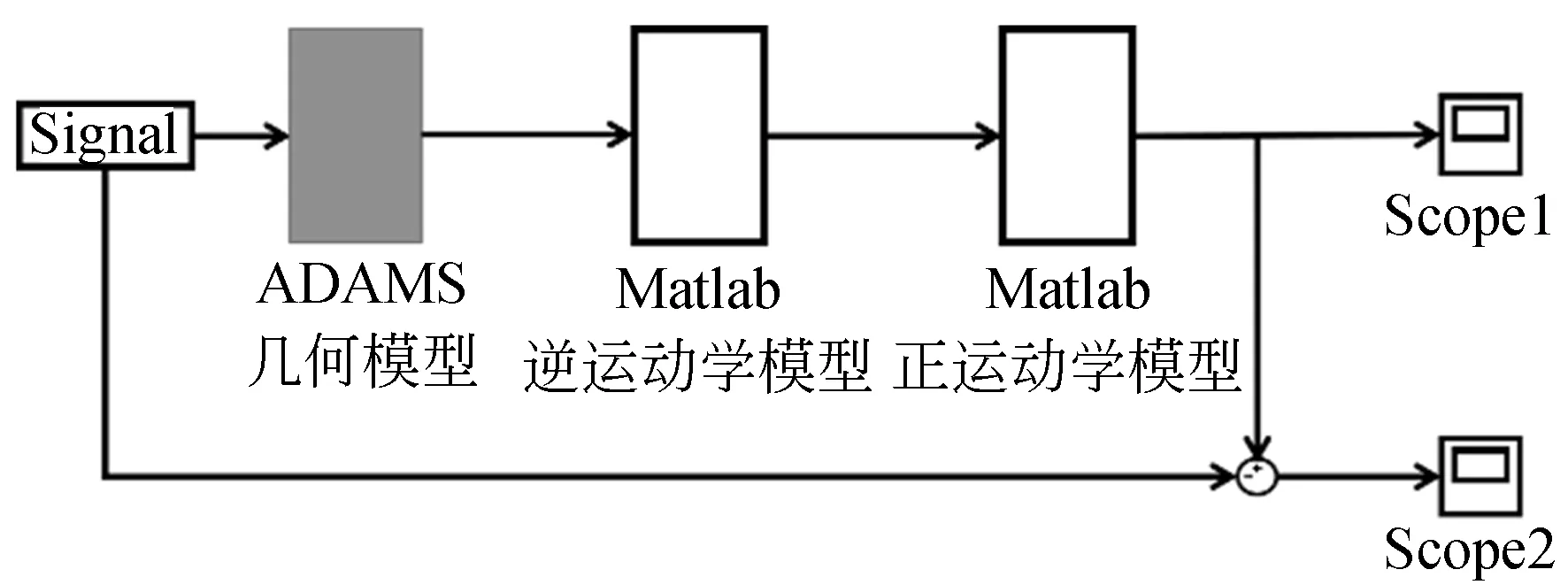
图5 逆运动学仿真系统Fig.5 Inverse kinematics simulation system

给定光电平台内框架系统负载的姿态角度(R,P,Y)，能够得到系统转动副的转动角度(α0,α1,α2)。借助上文已经验证的正运动学模型，对逆运动学模型进行验证，得到的误差曲线如图6所示。由仿真结果可知，串联球面机构逆运动学模型正确。

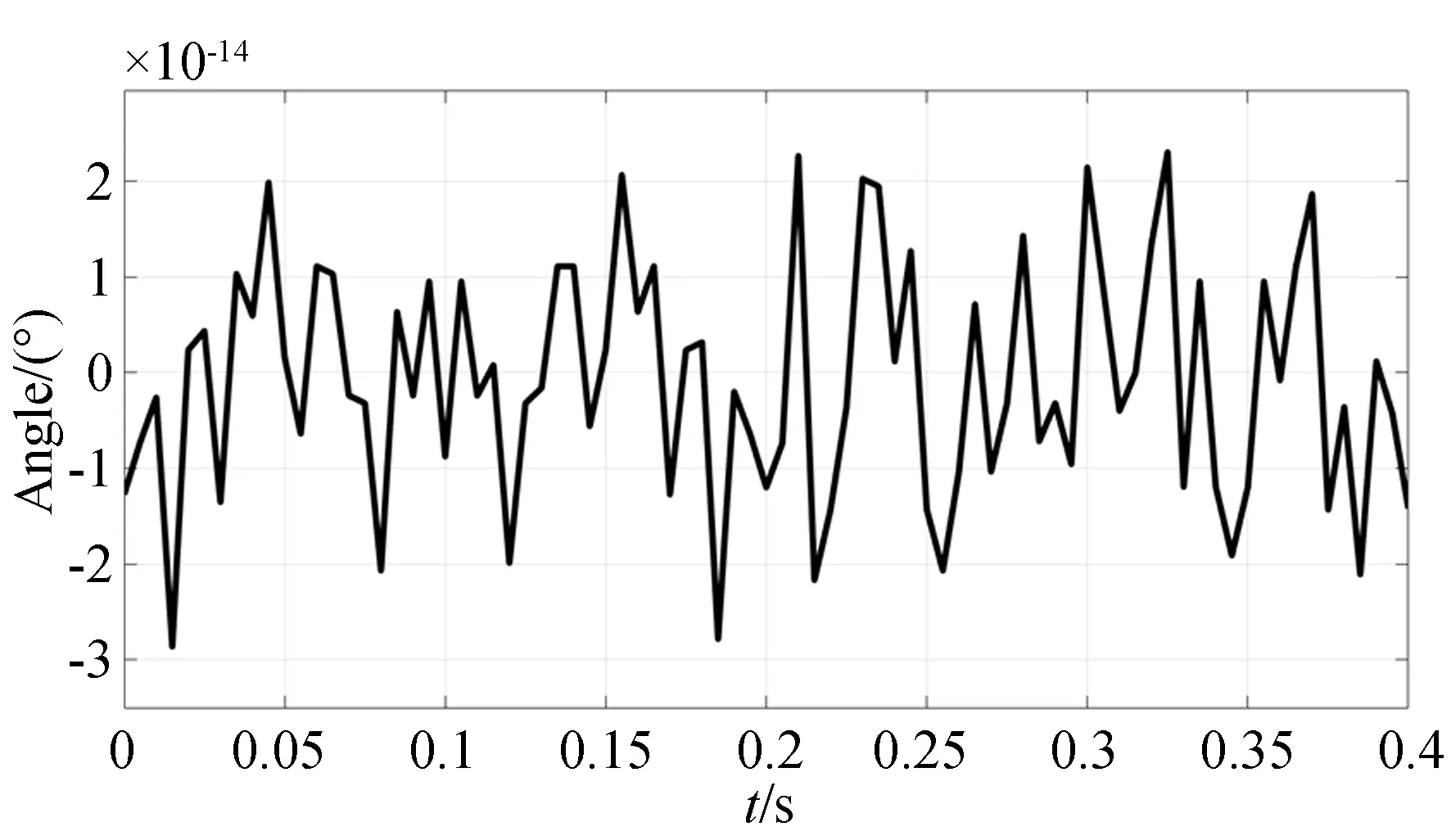
图6 逆动力学输出误差Fig.6 Inverse kinematics output errors

由于ADAMS与MATALB两款软件的数值精度不同，仿真结果存在一些误差，如图4和图6所示，但误差极小，可以忽略。通过多体动力学软件与MATLAB按照正逆运动学模型的计算结果进行比对可知，模型准确描述了机构的运动特征，解算准确。

4 实 验

本文对面向机载光电平台的串联球面机构进行了运动学模型验证，实验装置实物图如图7所示。

图7 串联球面机构运动学验证装置Fig.7 Series spherical kinematics verification device

实验装置利用带有轴承的驱动电机作为转动副。在每个转动副上安装了角度编码器测量转动副的相对转动角度；在负载框架底部安装了惯性测量单元(Inertial Measurement Unit, IMU)用于测量光电平台负载框的位姿。通过采集编码器和IMU的数据，经过前文建立的运动学模型的解算和对比，对机构运动学模型进行实验验证。

4.1 正运动学模型验证

给定串联球面机构电机幅值为6°的正弦指令控制3个转动副旋转；同时，比较IMU采集得到负载姿态实测数据与利用编码器角度和正运动学模型计算数据，结果如图8～图10所示，误差曲线如图11所示。

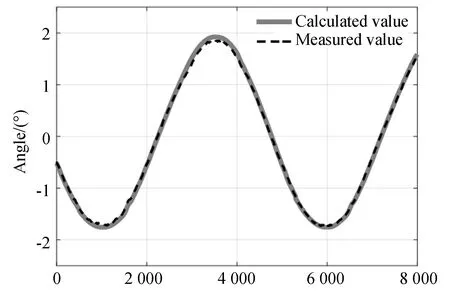
图8 负载的滚转角度Fig.8 Roll angle of load

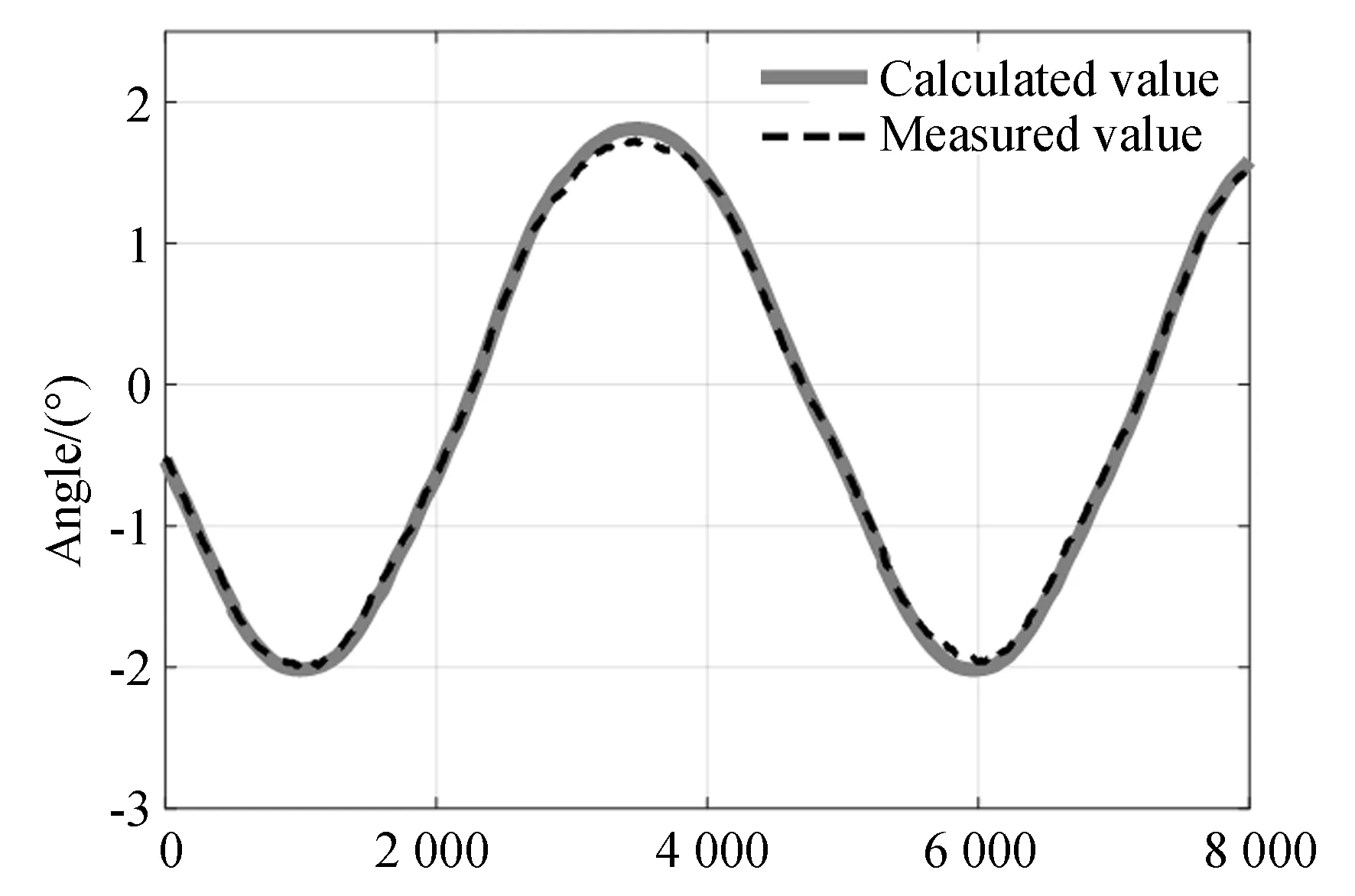
图9 负载的俯仰角度Fig.9 Pitch angle of load

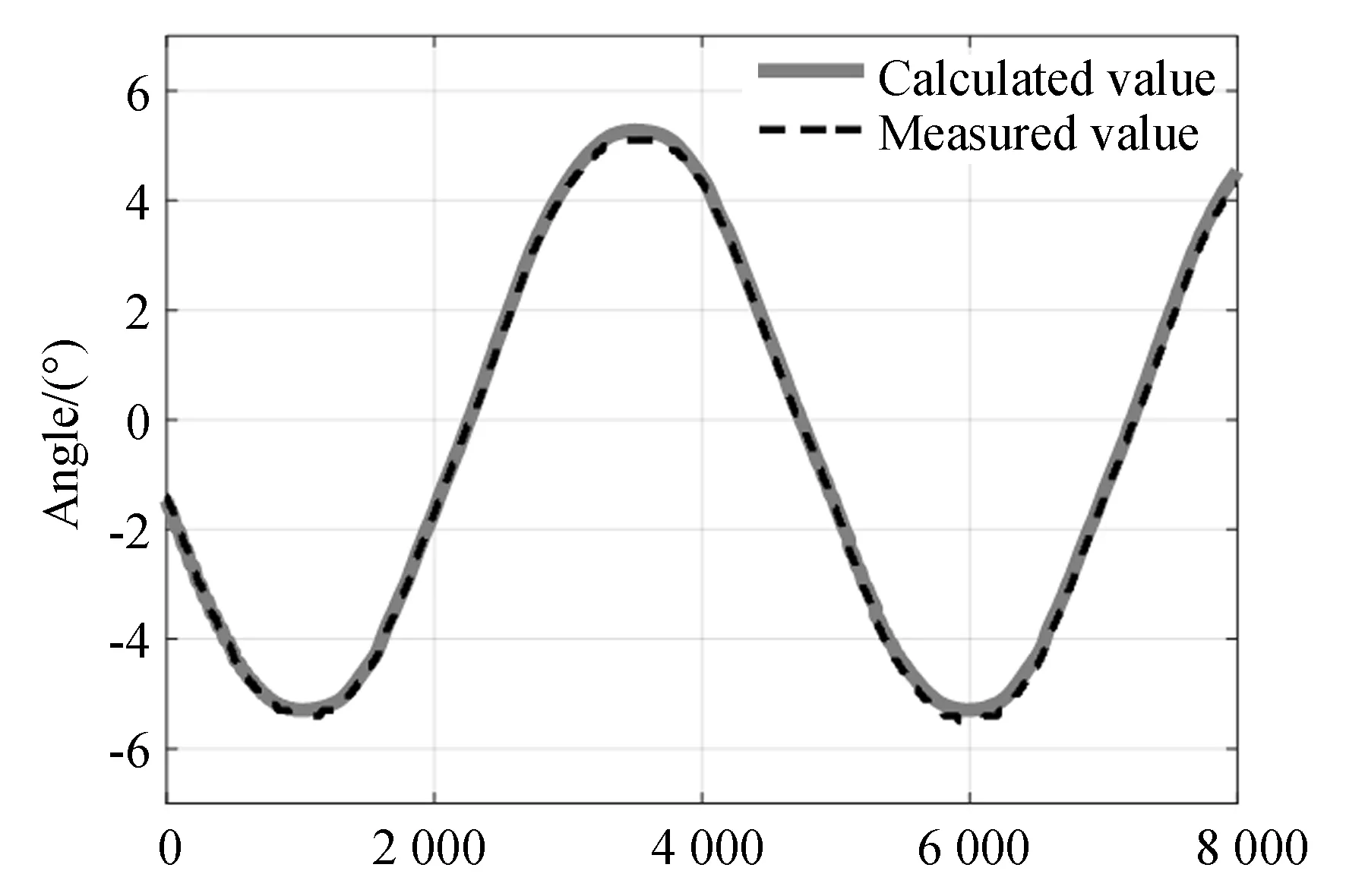
图10 负载的方位角度Fig.10 Yaw angle of load

图11 负载角度误差Fig.11 Load angle errors

经对比，正运动学模型的计算结果与实验装置实际测量值之间的误差在5%以内，误差幅值小于0.25°。这是由于所采用的测量原件自身精度有限(编码器动态精度为0.1°、微机电IMU动态姿态测量精度为0.2°)，实验装置加工和装配精度有限等造成的。

4.2 逆运动学模型验证

采集负载滚转、俯仰和方位角度信息，利用逆运动学模型计算转动副的转动角度，与编码器实际测量值进行对比，对比结果如图12～14所示，误差曲线如图15所示。

图12 转动副A的角度Fig.12 Angle of revolute joint A

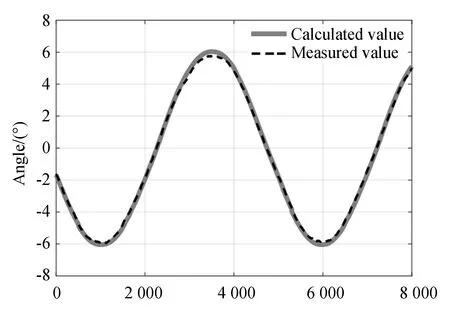
图13 转动副B的角度Fig.13 Angle of revolute joint B

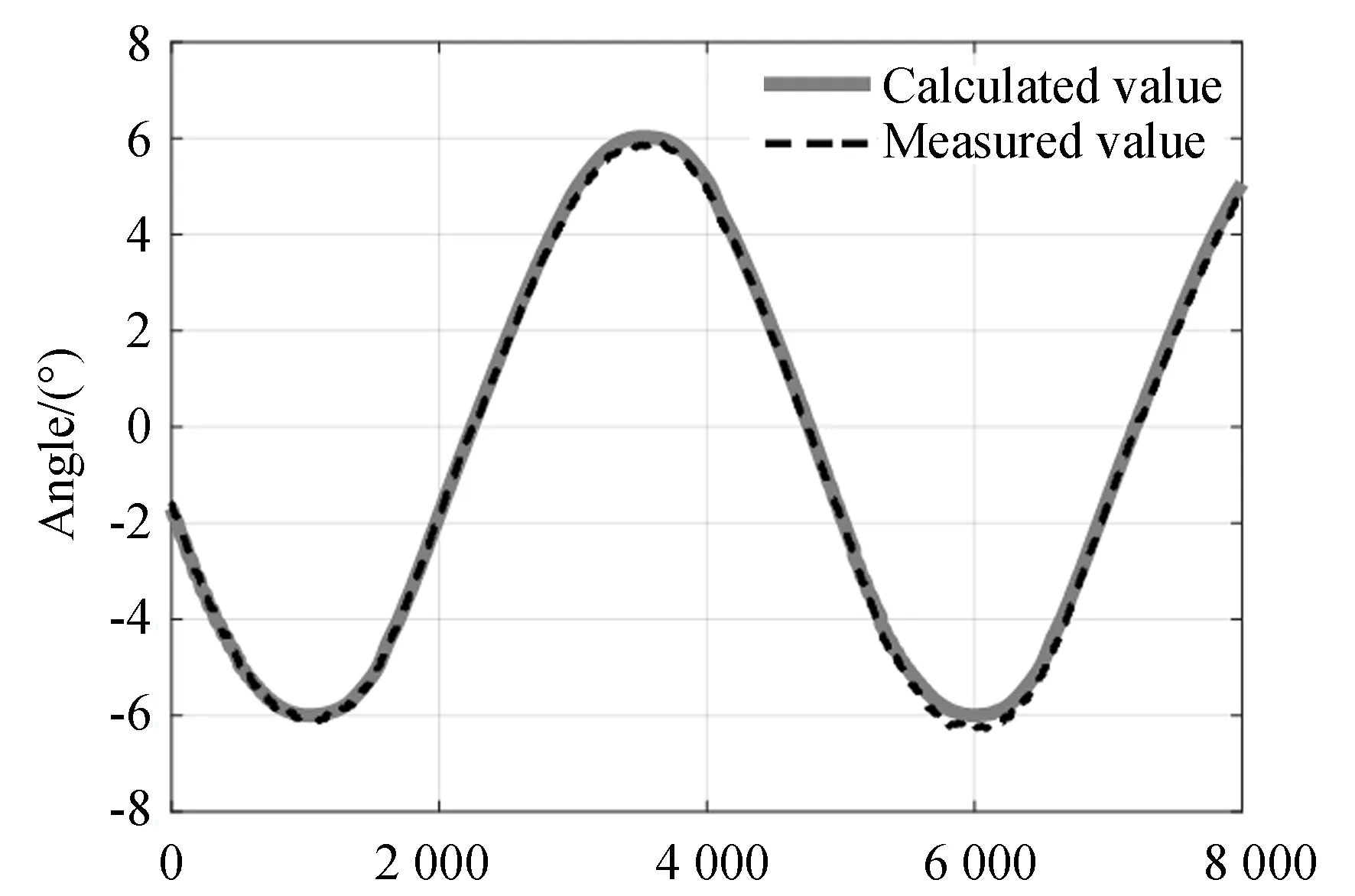
图14 转动副C的角度Fig.14 Angle of revolute joint C

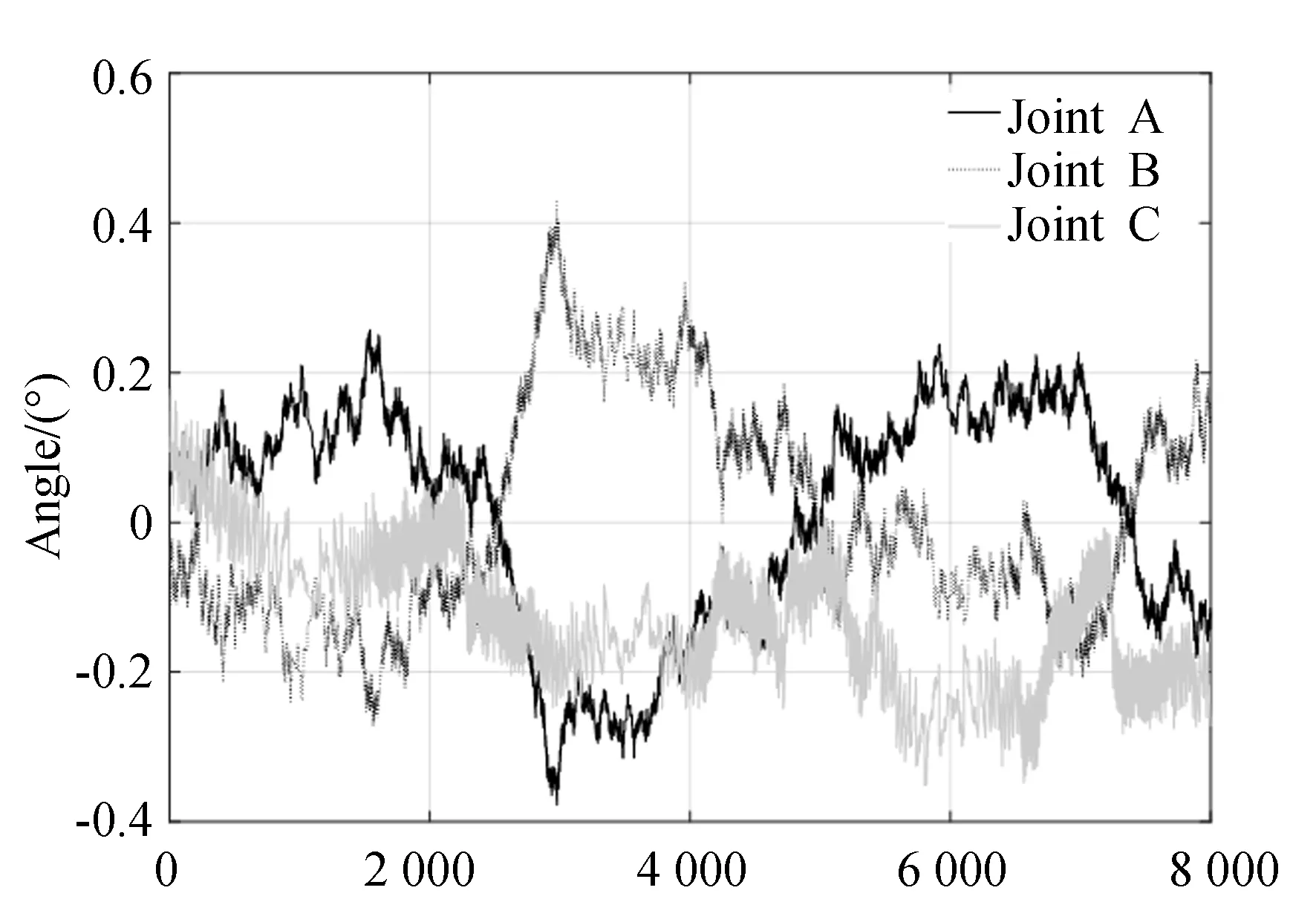
图15 转动副的角度误差Fig.15 Angle errors in revolute joints

经对比，逆运动学模型与实际模型误差也在5%以内。在实际机载光电平台设计中，要采用更高精度的编码器，并进行机械设计和工艺约束。

综合ADAMS仿真与在搭建的实验装置上采集的实测数据可知，本文基于D-H参数法建立的正、逆运动学模型是正确的，能够满足基于串联球面机构的机载光电平台视轴指向控制等实际应用需求。

5 结 论

为弥补面向机载光电平台的串联球面机构在运动学方面研究不足，借助机器人学领域的D-H参数法建立了简单、准确且易于解算的正、逆运动学模型，并通过ADAMS与MATLAB的联合仿真和实际实验验证了模型的正确性。

本文采用空间单链球面机构连接光电平台的基座和负载，有效节省光电平台内部的空间，有助于提升光电平台的载荷比。同时，串联连接方式较并联方式更易控制。该串联球面机构运动学模型为今后对串联机构动力学和控制学的研究以及进一步的工程应用奠定了基础。