厚度测量中对射激光束共线性视觉检测
李加福,朱小平,杜 华*,唐文彦
(1. 中国计量科学研究院,北京 100029;2. 哈尔滨工业大学 电气及自动化学院,黑龙江 哈尔滨 150001)
1 引 言
基于激光三角法的厚度测量方式,需要利用两个激光位移传感器测量工件的内外两侧,并由传感器间距减去两个示值计算出对应的厚度值[1-3]。为了使测量结果符合厚度定义,并且保证传感器间距标定结果的准确性,两个传感器的虚轴在测量前必须重合。但在实际中,如果不经过任何的调校措施,传感器的安装很难满足上述约束条件。因此,双激光束共线性的检测成为一个不容忽视的问题。
目前,激光束位姿检测方法已经取得了一定的进展。根据传感器的数量,检测方法可以分为单测头和双测头两种方式。其中,单测头激光束空间矢量的标定方法包括平面标定法[4]、球步距标定法[5-6]、等值球点标定法[7]以及在机视觉标定法[8]。它们的核心是由三维导轨带动传感器对某已知几何量进行测量,通过对该几何量的拟合计算反推激光束位姿。作为一种在机标定方式,它可以实现激光传感器坐标系与三坐标或机床坐标系的统一,但检测结果与运动轴精度有关。同时,该类方法对基准件、传感器方位旋转的要求,或者对激光束长度的约束,校准过程比较繁琐,不太适用于双传感器激光束共线性/相对位姿的校准。
对于双侧头测量轴线位姿的检测,依据传感器的安装方式,可以分为反向激光束或者对射激光束测量方法。在反向激光束的位姿检测方面,Yang[9]利用标准内圆对两激光束间的夹角进行了标定。刘新波[10]提出了基于阶梯状调校板的反向激光束共线性视觉测量方法,用于解决内径、平行平面间距的激光测量问题。其测量原理为沿基准方向平移摄像头,依据获取的光斑位置和平移距离计算出两个传感器光轴的相对位置关系。该方法需对两个光轴分别进行检测,并且,当使用两个对射安装的激光位移传感器进行厚度测量时,传感器间的有限工作距离也使得上述方法不再适用。
在对射激光束的位姿检测方面,周富强等[11]提出了基于未知运动平面靶的双传感器线激光视觉测量系统参数标定方法,其原理是利用平面靶标中的正方形顶点对传感器进行分别标定,该方法可不依赖于专门的空间坐标测量设备。为了实现基于双激光的植物叶片厚度检测,Lee等[12]提出了基于针孔的双激光束对准方法。将带有针孔的标准件放置在两个传感器之间的不同位置,保证激光束都能够穿过针孔,可以实现两个传感器光轴在测量装置中的对准。显然,这种装配、检测分离的工作方式,不利于激光传感器的安装调整,并且存在精度低,无法数字化、可视化的缺点。
本文在分析激光束共线性最大允差的基础之上,利用图像处理可量化光斑中心坐标的优势,并结合棱镜的分光作用,提出了一种基于分光棱镜的对射激光束共线视觉检测方法,旨在通过计算摄像机获取的激光光斑中心坐标来判断激光束之间的相对位置关系。
2 激光束不共线对厚度测量精度的影响
采用激光位移传感器进行回转壳段、平行平板厚度测量时,激光束不共线对应的4种测量误差模型如图1所示。其中,A和B对应为两个传感器的测量起始点,并且两点之间的距离AB已知,A1和B1为激光束与截面之间的交点(实际测量点),曲率截面圆心为O,两条激光束之间的夹角为α。
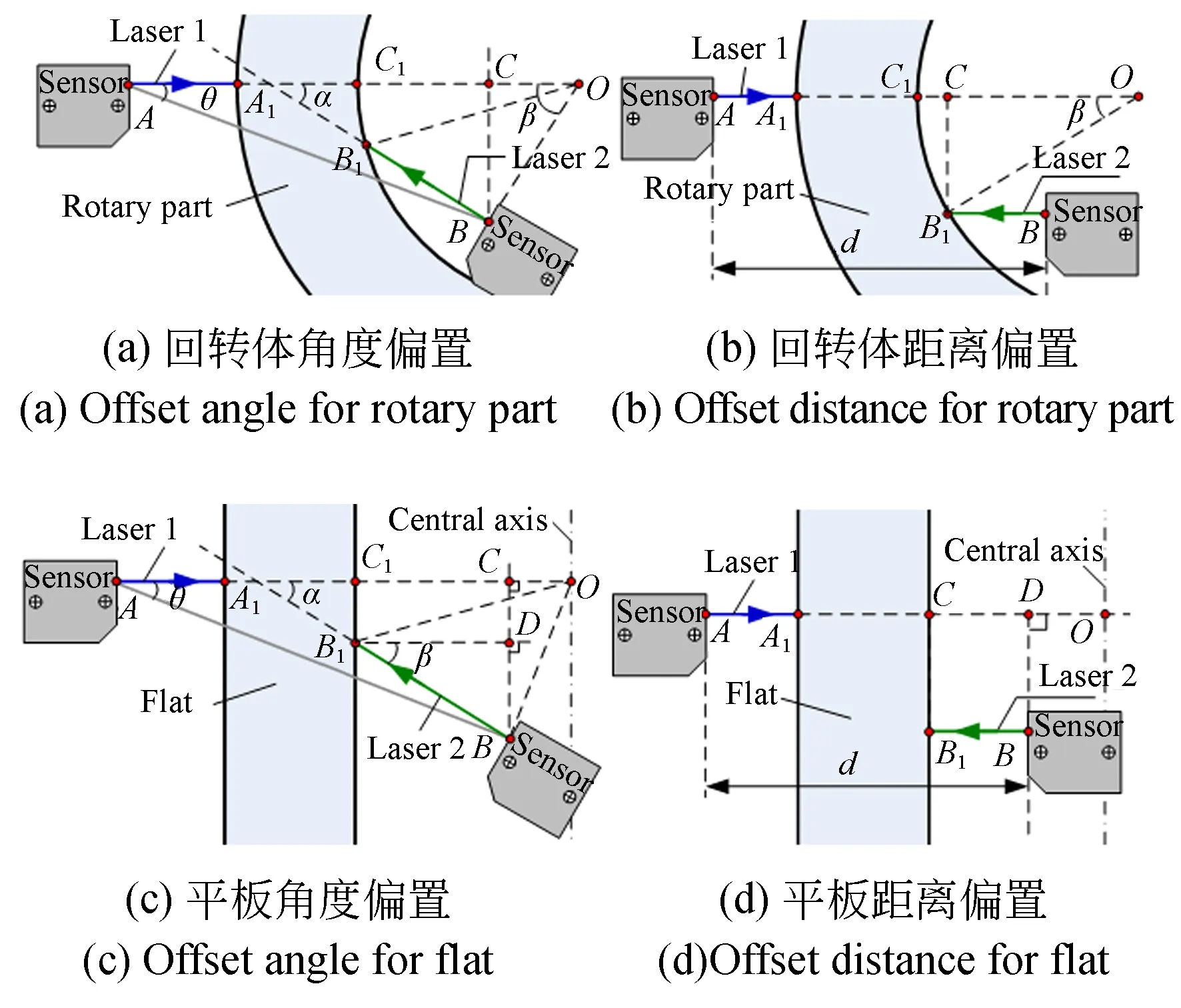
图1 激光束不共线时厚度测量示意图Fig.1 Thickness measurement with non-collinear laser beams
对于回转类壳段而言,其厚度测量误差为:
Δx=R-
AB×(cosθ-1)+BB1×(1-cosα).
(1)
当内径OC1的变化范围为100~1 100 mm,理论厚度A1C1的变化范围是2~22 mm时,激光束夹角引起的厚度测量误差如图2(a)所示。当传感器位置和圆筒状壳段内径不变时,被测件厚度越小、轴线夹角越大,测量误差就越大,且最大值不小于45 μm。当激光束测量线夹角不大于0.25°时,它引起的厚度测量误差在0.25 μm以内。当两条激光束间距的变化范围是0.5~3.0 mm时,不同激光束间距引起的厚度测量误差如图2(b)所示。壳段内径越小、平行激光束间距越大,测量误差就越大。当激光束测量线间距不大于0.22 mm时,它引起的厚度测量误差在0.25 μm以内。
对于平行平板而言,厚度测量误差等于Δx=AB(cosθ-1)+BB1(1-cosα)。假设AB=25 mm,θ=0.1°,两条激光束轴向夹角α的变化范围是0°~4°,理论厚度AC1的变化范围是2~22 mm,此时激光束不共线引起的厚度测量误差曲线如图2(c)所示。当其他参数不变时,被测件厚度越大、轴线夹角越大,测量误差也就越大,且误差不大于50 μm。同时,激光束测量线夹角不大于0.25°时,它引起的厚度测量误差小于0.25 μm。另外,激光束间平行不重合时,测量结果只与平板表面形貌有关。
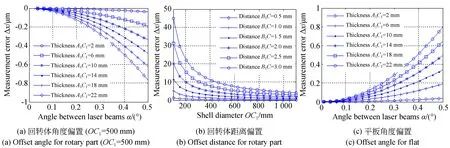
图2 激光束不共线时厚度测量误差曲线Fig.2 Thickness measurement errors caused by non-collinear laser beams
上述分析证明了调校激光光轴的必要性。同时,对于厚度大于2 mm的部件而言,为了保证厚度测量误差小于1 μm,两条激光光轴之间的夹角应小于0.25°,传感器测量线之间的距离应小于0.1 mm。这为厚度测量中激光束的共线调整提供了理论依据。
3 基于分光镜的激光束方向测量原理
3.1 基本原理
激光位移传感器激光束共线测量装置的结构及原理如图3所示。该测量装置主要由光学成像系统、支架、两个分光棱镜、反光镜和微动平台组成。其中,将微动平台的移动方向作为基准方向,并保证分光镜的激光入射面与该基准线垂直。另外,在共线性测量装置中,分光镜1、分光镜2、反光镜和接收屏幕都利用支架3固定在微动平台上。当微动平台移动时,能够在保证分光镜与接收屏位置关系固定的前提下,改变测量装置与激光器之间的相对位置,进而获取不同位置的激光束光斑中心。
借助于分光镜的半透半反功能,传感器1发出的激光束首先进入分光棱镜1,在经过棱镜1、棱镜2和反光镜之后,会在CCD接收屏上产生两个椭圆光斑A1,B1。根据激光在两个分光棱镜中的传播规律,可以将两个光斑中心的连线作为激光束在分光镜中的传播路线。同理,激光位移传感器2发出的激光首先射入分光棱镜2,光学成像系统也会采集到该光束对应的两个光斑A2,B2。利用计算机提取光斑中心坐标,便能计算出当前测量位置两条激光束之间相对位置关系。
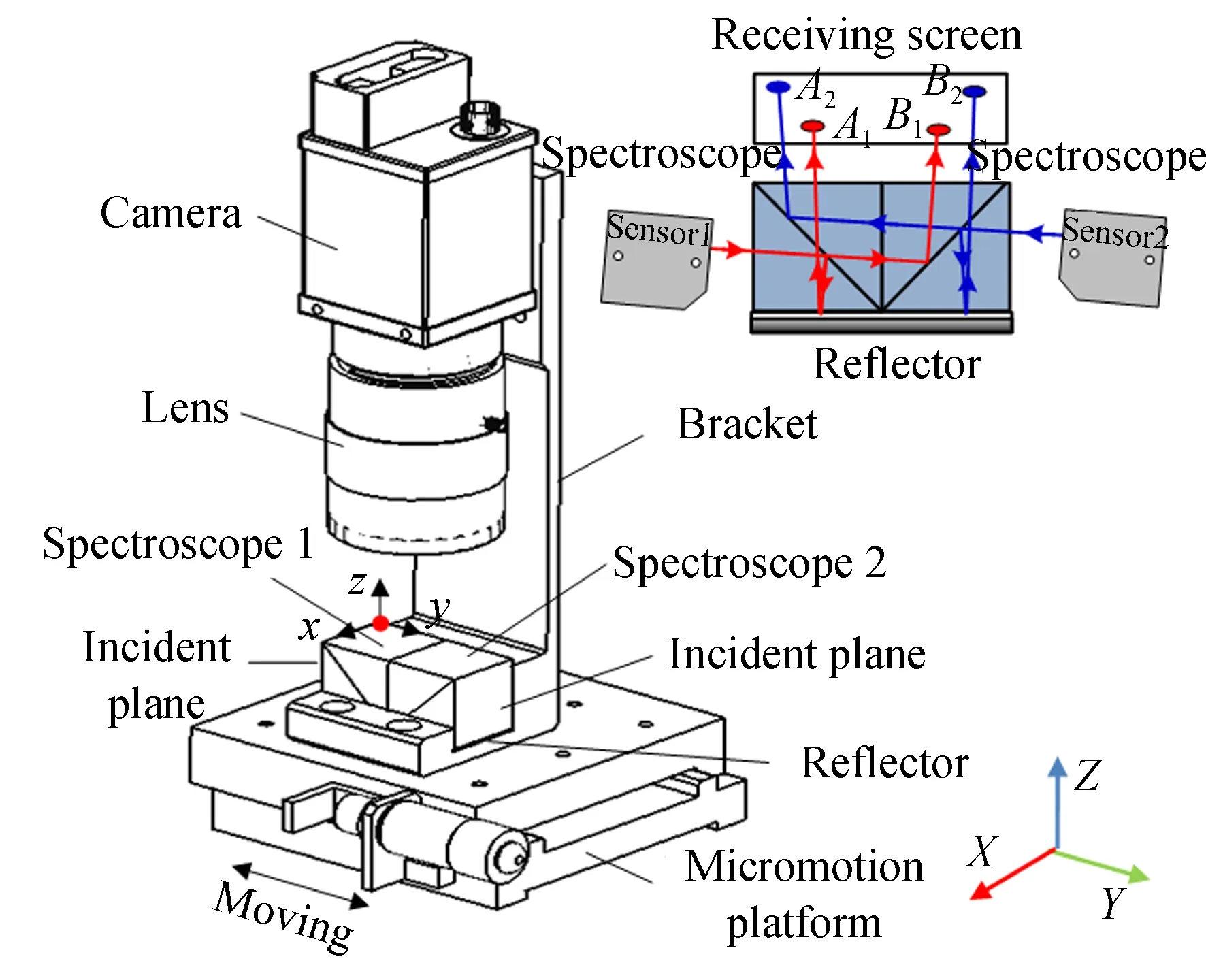
图3 激光束共线测量装置示意图Fig.3 Schematic diagram of laser collinear measuring devices
显然,为了确立光斑中心坐标与激光束空间位姿之间的关系式,需要对激光束在两个分光棱镜中的传播规律进行分析。根据分光镜1的顶点及其相邻的垂直边,建立了分光镜坐标系o-xyz。为简化分析过程,下一节对激光束在xoy,yoz两个平面内的传播规律分别进行讨论。
3.2 xoy平面内激光束传播规律
当激光束在xoy平面内的入射角为θxoy,在yoz平面内的入射角为90°,并且忽略两个分光镜间隙对光路的影响时,激光传感器1的传播路径如图4所示。其中,C1F1为理想状态下的激光束传播路线,C1D1是考虑分光镜折射率时的激光束传播路线。并且,传感器入射光线和出射光线相互平行,两光线之间的距离表达式为:
(1)
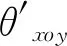
通常,分光镜的材料为K9,折射率为1.514,式(1)中的距离表达式可以简化为:
d=0.339 5L×sin 2θxoy.
(2)
因此,只要传感器2发射的激光束与激光器1的出射光线D1E1共线,便能保证两个传感器对应的光斑中心分别重合。这种光斑重合关系不会随着测量装置位置的改变而变化,即光斑重合是保证两条激光束共线的必要条件。
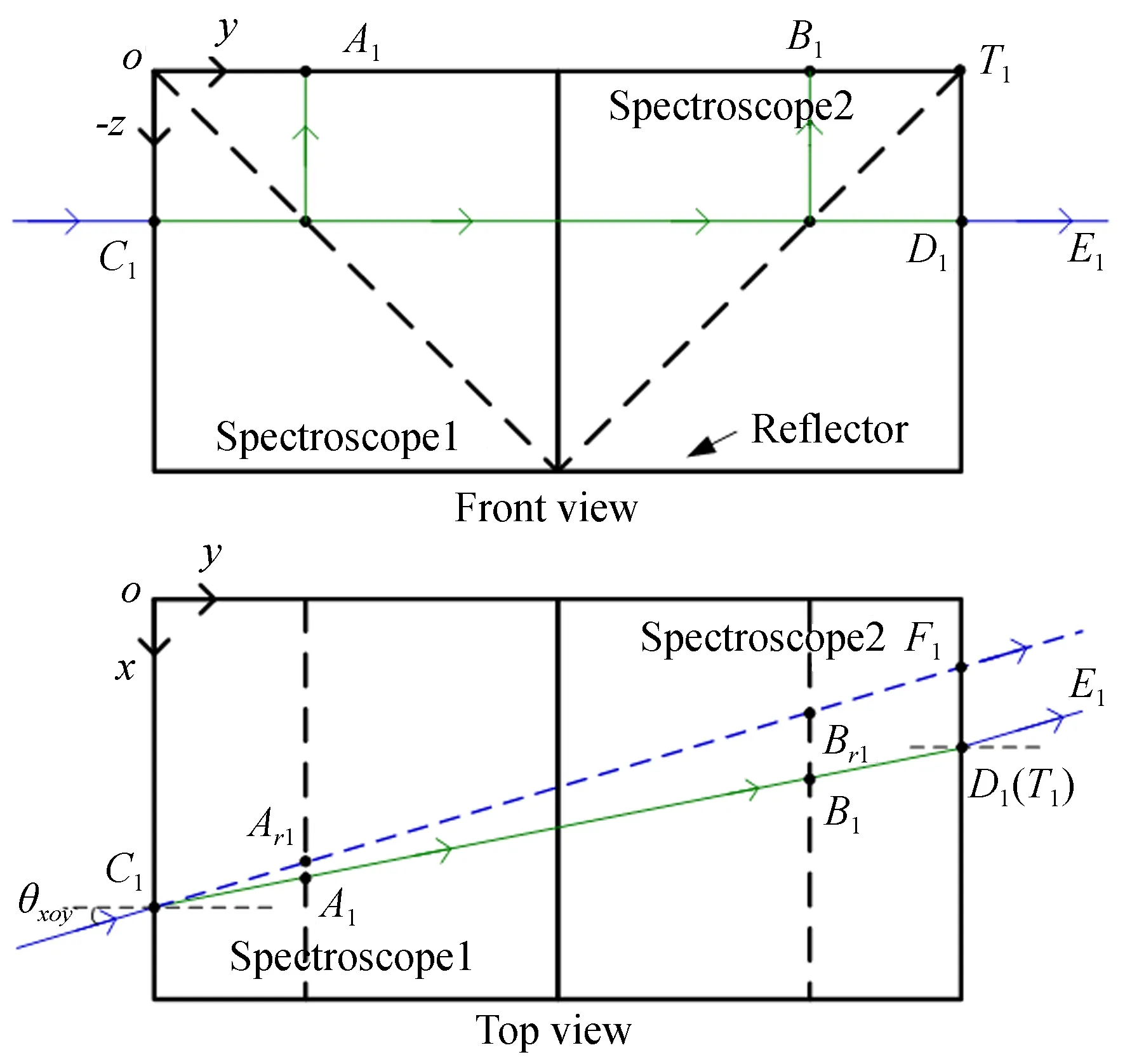
图4 激光在xoy平面内的传播路径Fig.4 Laser propagation path in plane xoy
另一方面,假设在o-xyz坐标系下激光入射点C1的坐标为(xc,yc,zc),光斑A1的中心点坐标(xa,ya,za)可表示为:
(3)
光斑B1的中心点坐标(xb,yb,zb)可表示为:
(4)
根据式(3)和式(4),推导出光斑间距|A1B1|的表达式为:
(5)
实际光斑A1,B1与理论光斑Ar1,Br1的距离为:
(6)
由式(3)~式(5)可知,当测量装置沿基准方向y移动距离l时,激光束入射角θxoy保持不变,点A1,B1,C1的x轴坐标发生变化,且大小等于tan(θxoy)×l,距离A1B1始终不变。因此,利用几何法对图4中激光束在xoy平面内的传播规律进行分析可以得出两个主要结论:(1)在进行激光束测量时,两个传感器对应的光斑中心分别重合是保证传感器光轴共线的必要条件;(2)当测量装置沿基准方向移动距离l时,光斑中心x轴坐标随之改变,且大小等于tan(θxoy)×l,而两个光斑的中心间距保持不变。
3.3 yoz平面内激光束传播规律
当激光束在xoy平面内的入射角为90°,在yoz平面内的入射角为θyoz时,激光传感器1的传播路径如图5所示。假设在o-xyz坐标系下激光入射点C1的坐标为(xc,yc,zc),光斑A1的中心点坐标(xa,ya,za)可表示为:
(7)
(8)
根据式(7)和式(8),光斑间距|A1B1|的表达式为:
(9)
因此,当测量装置沿基准方向y移动距离l时,激光束1的入射角θyoz保持不变,点A1,B1,C1的y轴坐标会发生改变,且大小等于tan(θyoz)×l,而距离A1B1也会随之增加tan(θyoz)×2l。由于图3中激光器1的传播路线并不是中心对称,当传感器2的光斑A2,B2与激光器1的A1,B1重合时,传感器2的激光束入射角一定不等于激光束1的入射角θyoz。这也意味着当测量装置沿基准直线移动距离l时,点A2,B2的y轴坐标变化量不能等于tan(θyoz)×l,即随着测量装置的改变,两个传感器的光斑位置和光斑间距都会发生变化。
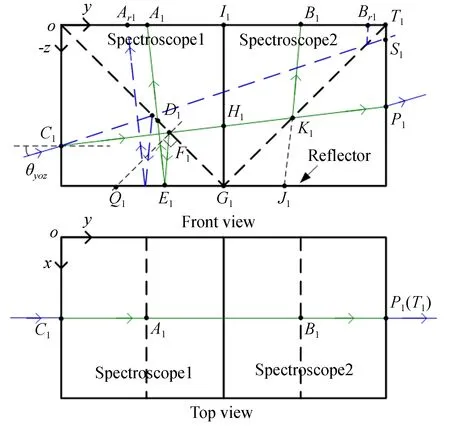
图5 激光在yoz平面内的传播路径Fig.5 Laser propagation path in plane yoz
另一方面,根据图5中的三角几何关系式,可推导出I1G1为激光在两个棱镜中形成的反射光线E1A1,K1B1的对称线。其证明过程如下:
∵∠E1F1G1=∠H1F1G1,∠E1G1F1=∠F1G1H1,F1G1=F1G1
∴ΔE1F1G1≌ΔH1F1G1。
∵∠H1G1K1=J1G1K1,∠H1K1G1=∠G1K1J1,G1K1=G1K1。
∴ΔH1G1K1≌ΔJ1G1K1,E1G1=H1G1=G1J1。
本研究经我院伦理委员会批准(批准文号:IRB-REV-2016005)。选择2014-09—2015-09因单个牙缺失在我院修复科拟行种植修复的患者109例,其中男59例,女50例,年龄19~72岁,平均(45.03±14.69)岁。
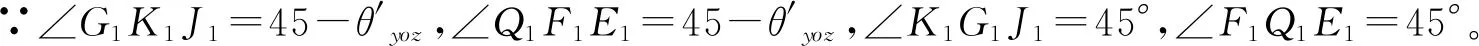
∵E1G1=G1J1,∠D1E1G1=∠G1J1K1,I1G1=I1G1。
∴I1A1=I1B1。
由于B1T1=T1P1,实际光斑B1与理论光斑Br1的距离为|B1Br1|,它与光斑A1以及入射角之间的关系为:
tan(θyoz).
(10)
即|B1Br1|可以表示为:
|B1Br1|=
(11)
同理,光斑A1与理论光斑Ar1的距离为:
|A1Ar1|=
(12)
利用几何法对图5中光束在yoz平面内的传播规律进行分析可以得出两个主要结论:(1)当测量装置沿基准方向移动距离l时,光斑中心的y轴坐标随之改变,且大小等于tan(θyoz)×l,两个光斑中心点距离增加tan(θyoz)×2l;(2)单条激光束在两个棱镜中对应的出射光线E1A1,K1B1关于边I1G1对称。
综上所述,双光轴共线判断的标准是:在xoy平面内保证两条光束共线的条件是两个传感器的光斑分别重合并且光斑中心坐标位置不会随着测量位置的变化而改变;在yoz平面内保证两条光束共线的条件是两个传感器的光斑距离在各个测量位置均相等。
4 图像坐标系下激光束位姿计算
前一节分析了激光束在分光镜三维坐标系o-xyz下的传播路线,但实际光斑中心的处理是在二维图像坐标系XOY下完成的。因此,需要计算图像坐标系下双激光光轴的相对位姿。

由于基准方向与分光镜坐标系o-xyz的y轴平行,故只需确定图像坐标系与分光镜坐标系之间的旋转角度ω。对式(3),式(4),式(7)和式(8)的分析可得,当测量装置移动时,在分光镜坐标系o-xyz下,单个激光束对应的两个光斑的基准方向坐标分量之和总是等于2L;在图像坐标系XOY下,该坐标分量之和是常数,即:
(13)
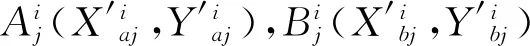
(14)
(15)
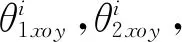
(16)
式中KCCD为图像采集系统的放大倍数。
根据公式(6),在不考虑折射率对光路的影响时,4个光斑中心的x轴坐标位置分别为:
(17)
根据式(17),在xoy平面内两光轴夹角αxoy的计算公式为:
(18)
根据式(18),在xoy平面内两光轴间距dxoy的计算公式为:
(19)
另一方面,根据激光在分光镜坐标系yoz平面内的传播规律可知,激光传感器1,2的折射角θi1yoz,θi2yoz分别为:
(20)
根据式(11)和式(12),在不考虑折射率对光路的影响时,4个光斑中心的y轴坐标分别为:
(21)
根据式(21),在yoz平面内两光轴夹角αyoz为:
(22)
根据式(22),在yoz平面内两光轴间距dyoz为:
(23)
5 实 验
5.1 共线性测量实验

图6 光轴共线性测量装置Fig.6 Measurement device of optical axis collinearity
激光束共线测量实验装置如图6所示,利用该装置对两个激光位移传感器之间的相对位姿进行了调节和测量。传感器型号为德国米铱ILD1700-10LL,测量范围为10 mm。摄像机的型号为MER-500-7UM/UC,通过USB将采集到的两条激光束对应光斑传输给计算机,经标定后光斑图像单个像素对应的实际尺寸为0.02 mm。在实验中,仅需要采集厚度测量范围内的激光光斑,即在微动平台示值为5,10,15,20处分别对光斑中心进行测量。在测量前,需要粗调激光位移传感器与测量装置之间的位置,使其中一个传感器的示值在-5 mm左右。整个测量过程进行了3次重复性测量。对光斑中心的提取采用多阈值加高斯拟合的方法[13-14],表1,表2分别为在不同测量位置获取的传感器1和传感器2对应光斑的中心坐标。
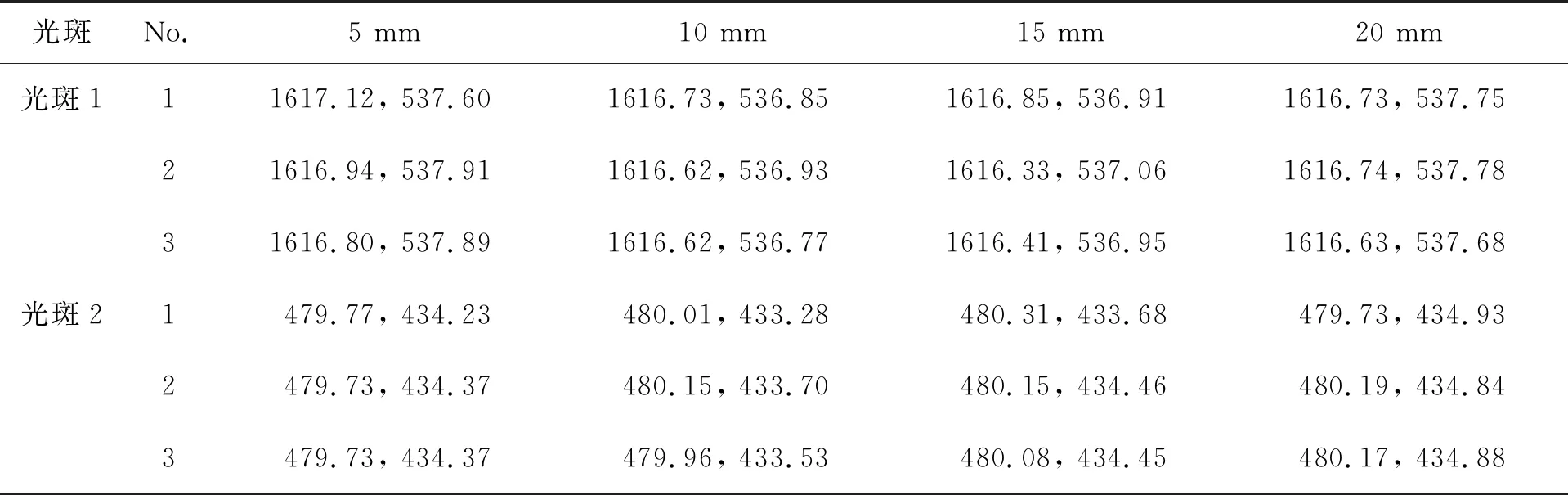
表1 图像坐标系XOY下激光束1光斑中心的测量结果
根据第4节双激光束位姿的计算方法,获取的两个传感器测量线之间的相对位姿关系如表3所示。从表3可知,两个传感器测量线之间的夹角最大为0.17°;在有效测量范围内,两条激光束之间的位置差最大为0.05 mm,满足激光束共线性最大允差的设计要求。从3组测量结果中可以发现,该测量方法具有较好的重复性。
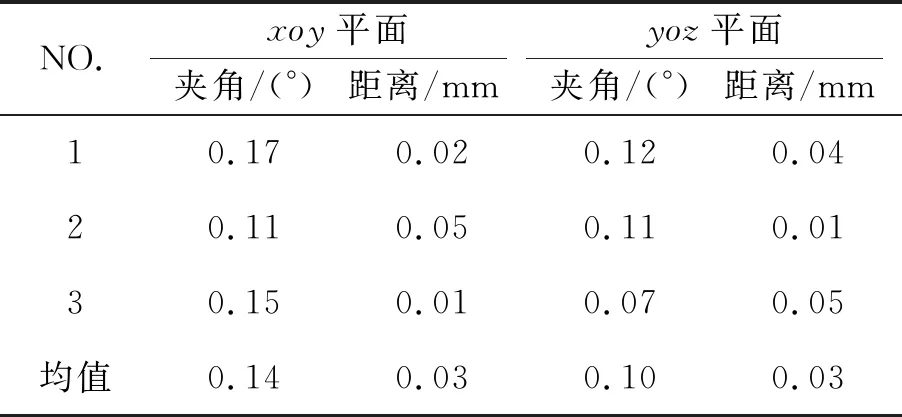
表3 棱镜坐标系o-xyz下激光束相对位姿测量结果
5.2 厚度测量实验
两传感器间的初始距离值是进行厚度测量的前提。因此,本文首先利用10,0.5 mm的标准0级量块(研合后标准距离值为10.5 mm)对传感器间距进行了标定,5次测量结果表明传感器间距为9.908 8 mm,标准差为0.001 1 mm。

图7 基于量块的厚度测量实验Fig.7 Thickness measurement based on gauge block
在此基础上,采用不同尺寸的量块对调节前后的厚度测量结果进行了对比实验,实验结果如表4所示。经过调校后,传感器组合对各种尺寸量块的测量误差明显减小,测量值和量块标称值间的差异小于4 μm。由于第2节中关于平板厚度测量理论的推导并未考虑传感器自身精度(测量重复性小于3 μm)、人为操作等因素的影响,此次实验数据大于理论分析的结果。
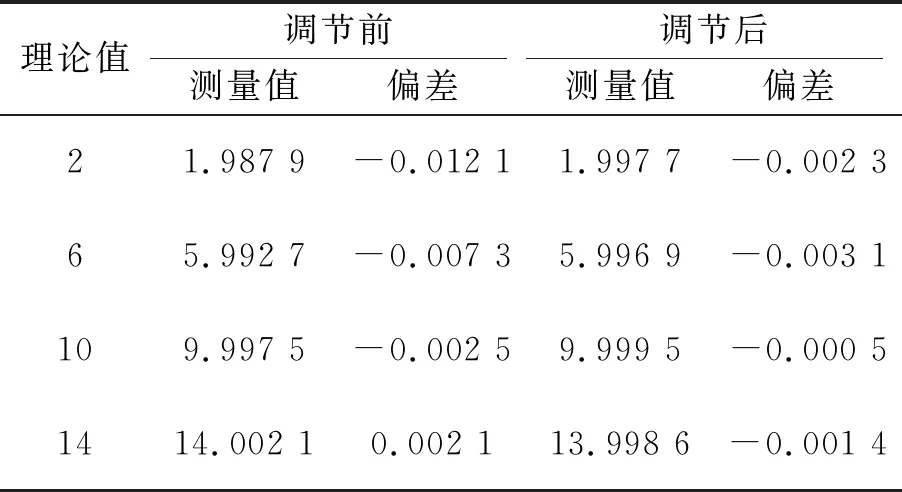
表4 调节前后厚度测量结果对比
6 结 论
本文针对对射激光束共线调节这一基于两个位移传感器厚度测量中的共性核心问题,提出了一种基于双分光棱镜的激光束空间视觉定位方法。本文重点分析了光线在两个分光镜上形成的平面光斑图像及其坐标分布规律,借助于图像坐标系与棱镜坐标系之间的转换关系,建立了4个光斑图像中心点坐标与两个传感器测量线相对姿态间的数学模型。对两个传感器共线性的测量实验表明,激光束之间的夹角不大于0.17°,距离不大于0.05 mm,满足厚度测量的要求。利用调节后的传感器对多种尺寸的标准量块进行了重复测量,厚度测量误差减小到4 μm,间接验证了共线调节方法的有效性。与现有对射激光束共线性测量方法相比,所提方法具有高精度、数字化、可视化可溯源的优势,并且可以辅助激光位移传感器的安装与调节。

