几何问题中的图形结构和数学运算
湖北省武汉市华中科技大学同济附中(430030) 王凯旋 严翠
我们知道数学核心素养包括:数学抽象,逻辑推理,数学建模,运算能力,直观想象,数据分析.六个核心与初中平面几何的图形研究:形状,位置,大小三要素的有机结合,可以提炼出:以“图形结构(数学抽象,数学建模,直观想象和图形的形状,位置的融合)—数学运算(逻辑推理,运算能力与几何图形大小的融合)”为思维模式的问题解决方法.具体方法为:首先,明确“已知结构”及包含的“已知运算”;其次,解决问题时,其路径为把“已知结构”转化为“目标结构”;“已知运算”转化为“目标运算”,从而达到问题的解决.
例1(2018年山东滨州中考第19 题) 如图1,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若求AF的长.

图1

图2
解在对试题条件和结论进行分析时,我们不应仅仅关注45◦角,还应该关注45◦角所在的几何图形形状.更需要关注几何图形的整体结构.这里和试题比较相近的一个图形结构就是:正方形ABCD中含有以点A为角顶点的45◦角(如图3,4).这是我们在正方形问题中研究比较多的一个几何图形结构,这个结构对应的数学运算有很多,其中一个基本运算:BP+DF=PF仅仅通过全等就可以得到.如果利用这个几何图形结构相对应的数学运算来解答此问题,应该算一种比较自然的解法,同时解答过程比较简单.
如图2,把矩形ABCD补成正方形AMND,延长AE交MN于点P,连接EP.得到基本结构:正方形AMND中含有以点A为顶点的45◦角; 从而有基本运算:MP+DF=PF,在正方形AMND中易得:∆ABE∆AMP,则又∵AB=2,AM=4,BE=1,∴MP=2,则MP=2,设DF=x,由基本运算得:PF=MP+DF=x+ 2,NF=4−x,在Rt∆PNF中,PN2+NF2=PF2即:22+(4−x)2=(x+2)2,解得:;在Rt∆ADF中,,
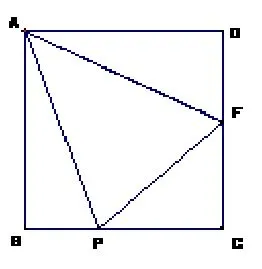
图3
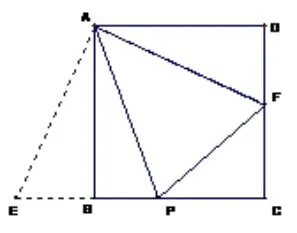
图4
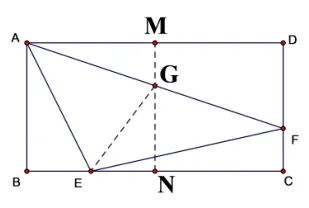
图5
如图5,分别取AD,BC的中点M,N,连结MN交AF于点G,连结EG,易知四边形ABNM是正方形,设MG=x,∴GN=2−x,∵BE=1,∴EN=BN−BE=1,在正方形ABNM中,∠EAF=45◦,由半角模型可知:EG=MG+BE=x+1,在Rt∆ENG中,(2−x)2+12=(x+1)2,解得,即∴∵MG//DC且M是AD中点,∴G是AF中点,∴.
例2如图6,若点M,N分别在正方形ABCD的边BC,DC的延长线上,且∠MAN=45◦,请探求S∆AMN,S∆ABM,S∆ADN之间的等量关系,并证明;
(2)如图7,在∆ABC中,∠MAN=45◦,且AD⊥BC于D,若BD=3,CD=10,求S∆ABC.
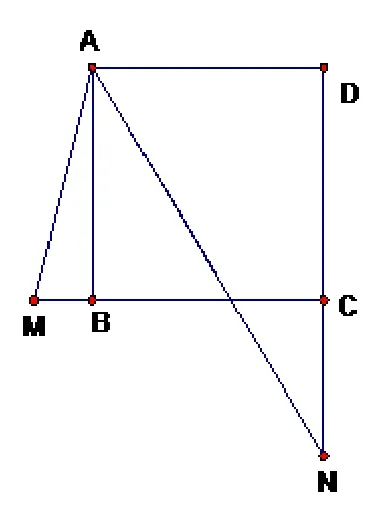
图6

图7
解如图8,在DC上截取DQ=BM,连接AQ,∵四边形ABCD正方形,∴AB=AD,∠ABM=∠ADQ,∴∆ABM∆ADQ,∴S∆ABM=S∆ADQ,AM=AQ.
设∠BAM=∠DAQ=x,∠BAN=y,则x+y=45◦,∴∠QAN=90◦−(∠BAN+∠DAQ)=90◦−(x+y)=45◦,∴∠MAN=∠QAN,又∵AN=AN,
∵∆AMN∆AQN,∴SANM=S∆ANQ,∴S∆AMN+S∆ABM=S∆ADN.
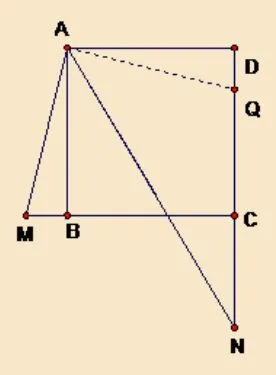
图8

图9
分析从第一问到第二问,从完整结构到残缺结构,第一问存在一个正方形的图形结构,而第二问只有一个三角形的图形结构,根据图形结构—数学运算的思维模式,保持第一问的相同图形结构和数学运算的方法,以AD为边,构造一个正方形试一试.
解如图9,以AD为边,在AD的右侧作正方形ADEF,在EF截取FQ=BD,连接AD,CQ,则AD=AF,∠ADB=∠AFQ,∴∆ABD∆AQF,则AQ=AB.
设∠BAD=∠FAQ=x,∠CAD=y,则x+y=45◦,
∴∠QAC=90◦−(∠DAC+∠FAQ)=90◦−(x+y)=45◦,
∴∠BAC=∠QAC,又∵AC=AC,∴∆ABC∆AQC,
∵BD=3,CD=10,∴QC=BC=13.
设CE=x,则EF=DE=10+x,FQ=BD=3,
∴QE=x+ 7,在Rt∆CEQ中,CE2+EQ2=CQ2,
即:x2+(7+x)2=132,解得:x=5,∴AD=DE=15,.
平时的训练时,就要注意总结几何图形的“图形结构”及其对应的“数学运算”.这样在解答问题时,才能抓住图形结构及数学运算顺利完成问题的解答.

