高中数学思维可视化对培养学生数学核心素养的案例研究
广东省湛江市教育局教育研究室(524000) 陈恒曦
1 思维可视化的内涵与外延
麦考尔米克等人于1987年在撰写一份报告时正式提出“Visualization”这一专门术语,“Visualization”的意思就是“可视化”.到了20 世纪90年代,作为一门欣欣向荣的新兴学科,可视化技术有了长足的进步,例如微软公司的操作系统.现在,教育教学领域前后出现了图示可视化、思维可视化等崭新概念,可视化技术得到了广泛应用.有专家通过分析近20年间有关研究思维导图的论文,归纳了我国有关思维导图的研究思路和现状,证明了思维导图在教育领域是有效可行的.
华东师范大学的刘耀源教授曾经说过,思维可视化能够把原本不可见的思维路径、思考规律通过图示、图像等有机组合后进行科学呈现,使思维过程得以一目了然.思考的方法主要有区分、推理(演绎、归纳、类比)、抽象、概括、分析、综合等,还包括聚合、递进、发散等思考模式.在思考过程中,思维路径反映了思维发展的脉络和线索.在日常教学中,教师可以通过利用概念定义图、思维导图、流程图等图示化工具来实现思维的“可视化”,从而辅助教学.思维可视化的图示信息技术就如同一座桥梁,实现了思维从抽象到具象的搭建和跨越.鱼骨图、思维导图、概念图、流程图、模型图等是现今非常多见的图示技术,随着信息技术的不断纵深发展,现代教室已普遍多媒体化,思维可视化技术日益成熟并迅猛发展,为思维可视化教学奠定了物理基础.思维可视化技术在现阶段主要有生成图示的软件技术和交互式图示呈现技术,呈现图示的交互式工具包括电脑、投影仪、电子白板、交互式触摸显示器等,均可呈现出丰富的思维可视化教学资源,以实现学生与信息资源的多向立体互动.在实际教学中,教师使用交互式工具呈现教学内容以辅助教学,可以促进学生对知识的深刻理解,使学生体会思考的过程,进而学会分析和解决问题.
2 基于核心素养的思维可视化教学策略
在课堂上,指任课教师充分利用图像、图形、动画等一系列辅助工具和信息技术,将符合学生认知能力、规律的相应教学内容通过灵活的教学活动内化为学生的认知结构,即为可视化教学.思维可视化教学策略是指把以教学重心放在发展学生的思维能力上,通过可视化技术,将思维训练与学科教学进行深度融合的高效教学策略.
思维可视化教学策的常用图示方法有解题过程鱼骨刺图、学科思维发展导图和策略模型导图.思维可视化教学策略有以下三个要求:首先,不能过分关注画图而忽视学生的思维发展,尝试让学生对图示进行评价和改进,科学灵活地展现图示的生成过程;其次,教学过程中必须注重培养和提升学生的思维发散和聚合能力、图示技术应用能力和知识建构能力;再次,思维可视化教学策略的使用必须要遵循心理规律、思维发展规律、学科规律和考试规律.
3 高中数学思维可视化的案例分析
案例1向量的综合问题的可视化解题分析
(2020年广东省佛山市第一次教学质量检测数学理科试题第14 题5 分) 已知向量a,b满足|a|=1,|b|=2,记向量a,b的夹角为θ,则sinθ=____.
可视化解题流程:


点评本题涉及两个向量的模和夹角,利用向量模的公式、两个向量的数量积的定义以及利用|a|2=a2转化是求解的关键.本例题借助“思维导图”将题意进一步阶梯式分解和剖析,逐步展示解题的思维流程,形象直观地反映了大脑自然思考问题的解决步骤.
案例2立体几何的综合问题的可视化解题分析
(2020年浙江省杭州市第一次教学质量检测数学理科试题第18 题12 分) 如下图所示,已知三棱锥P-ABC,∠ACB=90◦,CB=4,AB=20,D为AB的中点,且∆PDB是正三角形,PA ⊥PC.
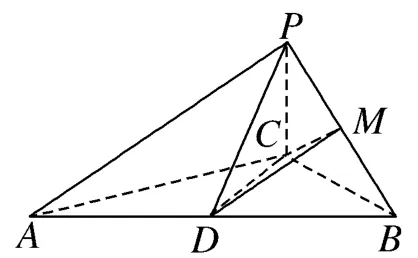
(1)求证:平面PAC⊥平面ABC;
(2)求二面角D-AP-C的正弦值;
(3)若M为PB的中点,求三棱锥M-BCD的体积.
可视化解题流程:


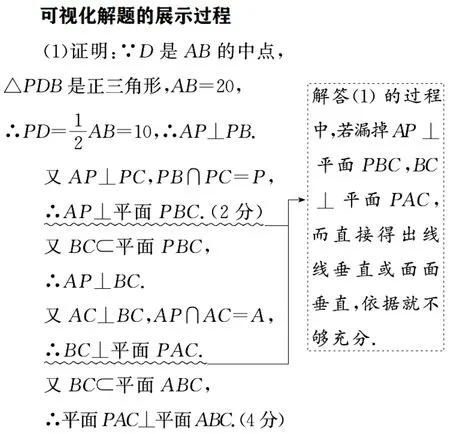


点评线面垂直肩负着承上启下的重任,是空间三种垂直关系的中枢,学生一旦形成“以线面垂直为中轴,寻找其它垂直”的思维导图,就可在垂直关系的证明、空间距离、几何体体积等问题上大展身手.“思维导图”是思维可视化的有效工具,能很好地指导数学教学:其一,利用“思维导图”将每个数学知识节点连接成网络,构建出完整的知识体系,方便学生去把握知识的脉络;其二,“思维导图”可以拓宽学生的思维界限,并应用于解答数学题目当中,令学生借助“思维导图”中的关键节点内容和桥梁来打开解题思路.借助“思维导图”,能够将题目的解答思路变得越发清晰,从而找出解决问题的最优化方案;其三,借助“思维导图”,有助于学生对解答思路进行总结与反思,“可视化”的作用显而易见.因此,教师若能在教学过程中,逐步培养学生形成解题前优先画出“思维导图”,将数学问题逐步分解剖析的思维模式,“思维导图”将能帮助学生更好地寻找出有效的解题思路与方法.
案例3解析几何的综合问题的可视化解题分析
(2020年福建省厦门市第一次教学质量检测数学理科试题第20 题12 分)已知动圆P过点A(2,0),且被y轴截得的线段长为4,记动圆圆心P的轨迹为曲线C.
(1)求曲线C的方程;
(2)若动圆P与y轴交于M,N两点,且|AM|<|AN|,求的最小值.
可视化解题流程:




点评利用方程的思想去研究曲线,利用曲线的性质去研究方程,是解析几何的核心要素.体现这一思想的重要表现形式包括有曲线轨迹问题、最值问题等等.在本题的分析过程中,正是充分运用了“思维导图”这一图形工具来将问题逐一展开,再深入分析和探求,将学生在思考过程中隐约模糊、难以言表的部分内容具象化、逻辑化、图形化、示意化,让学生的思考层层深入,拨开云雾,进而找到解决问题的关键节点,并顺着主、分枝干,上下求索,从而高效、便捷地破解难题.
4 结语
以笔者的理解,利用可视化教学策略是能够提升学生数学核心素养的.学科思维导图可以联系起零散的碎片化知识,逐步形成知识的系统结构,促进学生核心素养的发展.解题流程图主要用来分析复杂问题,将思考程序呈现出来,使得思路更加清晰可见;学科策略模型图可用于呈现数学学科的问题解决策略,引导学生“举一反三”、提升类比推理的思维能力.在不同发展阶段,学生的数学核心素养的层次水平自然不同,并且培养目标和方式也不一致.在中学阶段,学生的几何直观水平得到明显提高,开始逐步懂得表达复杂的数量关系,所以在此阶段最主要培养学生的是逻辑思维表达能力.学生数学核心素养的发展和获得必然是一个循序渐进的过程,随着学生的学习及自身发展需要而更新,并且不断深化,将伴随学生其一生的学习、工作和生活.

