一道三角形面积最值题的多角度思考

熊若凡

(江苏省前黄高级中学国际分校高三(6)班，213161)

数学解题不能只关心得到结果,而应该关注问题的求解过程.一个问题的多角度思考往往有助于拓展我们的思维,锻炼我们分析、解决问题能力.本文介绍一道最值题的求解与思考、体验的过程，供大家参考.

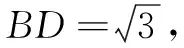
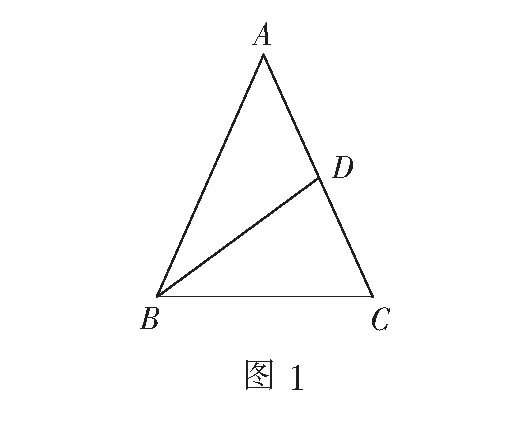
视角1关注余弦定理与三角函数

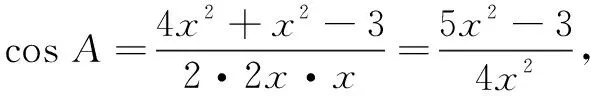
于是,由三角形面积公式，可得

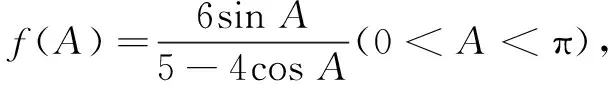
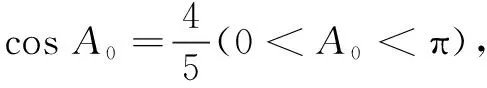
反思本解法利用导数判断函数单调性时,出现了零点不可求的情况,增加了问题求解难度.有没有更简单的方法?我们变换主元,可得如下简便解法.

视角2侧重余弦定理与二次函数

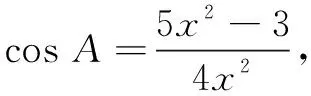
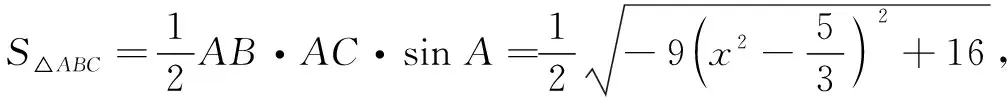
反思以上两种解法都是从代数的角度考虑问题,能否从几何的角度寻找解题思路?为此,我们又得到如下两种解法.

视角3利用三角形重心的性质

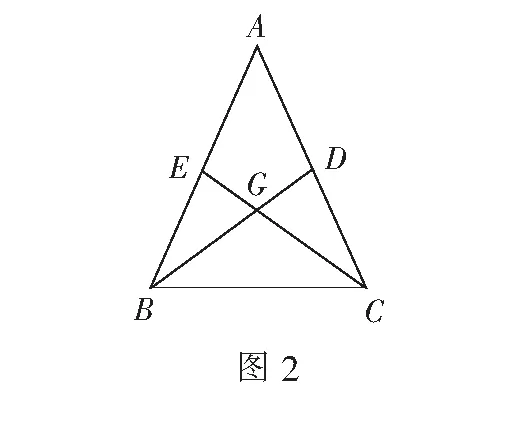
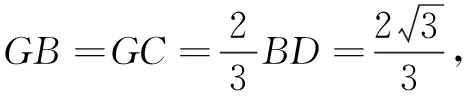
设∠BGC=θ,则

易见当sinθ=1时,S∆ABC取最大值2.

视角4借力阿波罗尼斯圆

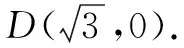
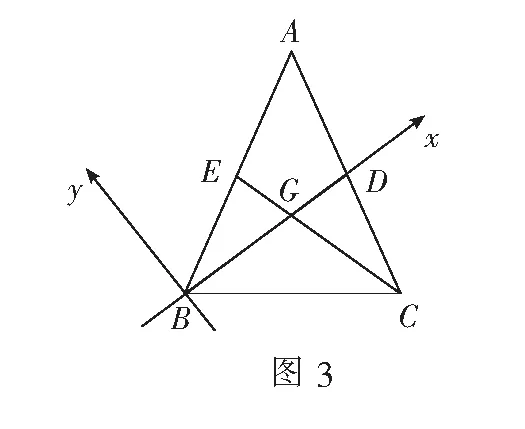
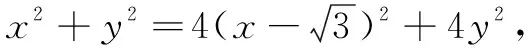
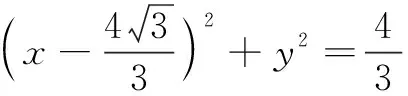
综上所述,在解题过程中只要我们勤于思考,适时转换观察问题的角度,就可以挖掘问题背后的隐含条件,化难为易,培养和发展我们综合处理问题的能力,在一题多解中择优处理,不断提升自身的数学核心素养.