用参数方程处理解析几何高考真题

周牛娃

(陕西省咸阳市乾县第一中学, 713300)

解析几何的综合问题,已知条件多,题干长,常涉及多个知识点,对学生的能力要求高,不少学生感到思路不清,难以入手.如果我们在解题中注重知识融合,有时会眼前一亮,解题思路会“柳暗花明”,起到事半功倍的作用.笔者研究近几年高考解析几何中的解答题,发现许多题都可用参数方程求解,并且大大减少运算量.

一、用直线的参数方程解题

例1(2018年全国高考题) 抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线l与C交于A，B两点,且|AB|=8.

(1)求直线l的方程;

(2)略.

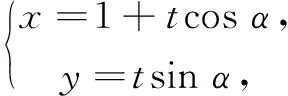
所以,直线l的斜率k=tanα=1,其方程为y=x-1.

反思通过例1可见,对于直线和圆锥曲线位置关系的综合问题,若直线过已知的定点,且其他的点、线段等都在过该定点的直线上,满足上述这两个条件时,可以考虑用直线的标准参数方程来解题.

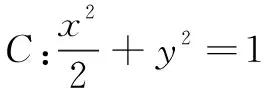
(1)当l与x轴垂直时,求直线AM的方程;

(2)设O为坐标原点,证明:∠OMA=∠OMB.

解(1)略.

=0,

即kMA=-kMB,所以∠OMA=∠OMB.

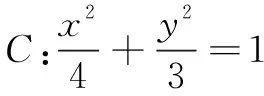
(2)略.

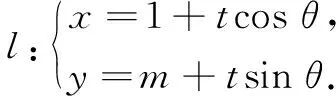
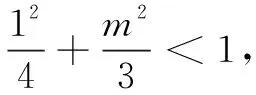
二、用圆锥曲线的参数方程解题

(1)若|AF|+|BF|=4,求l的方程;

解(1)12x-8y-7=0.(过程略)

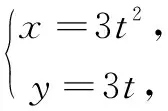
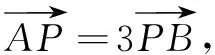
反思通过例4可以看出,对于直线和圆锥曲线位置关系的综合问题,如果直线没有经过定点,用直线的参数方程不方便解题时,我们可以另辟蹊径,采用圆锥曲线的参数方程解决问题.上述问题中用到了抛物线、椭圆的参数方程,再结合三角函数的有关知识,这些问题会迎刃而解.

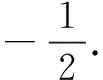
(1)求C的方程,并说明C是什么曲线；

(2)过坐标原点的直线交C于P，Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.

(i)证明:∆PQG是直角三角形;

(ii)求∆PQG面积的最大值.

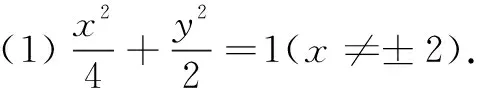
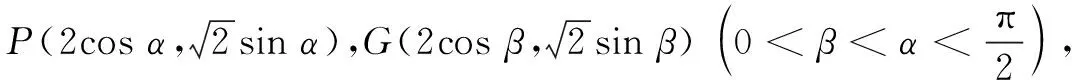
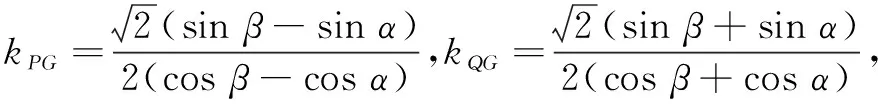
(ii)由(i)可知

S∆PQG=2S∆OPG

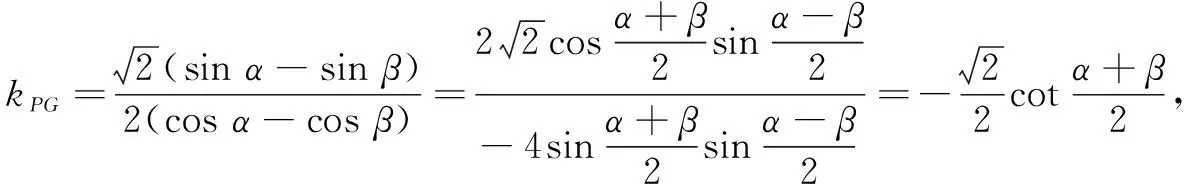
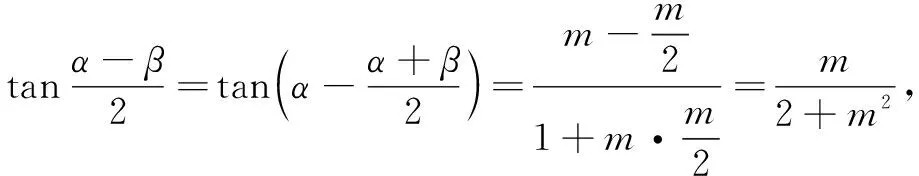
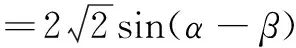
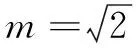
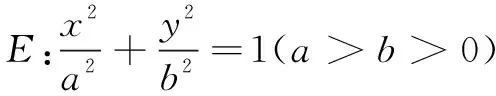
(1)求椭圆E的标准方程;

(2)若直线l1，l2的交点Q在椭圆E上,求点P的坐标.

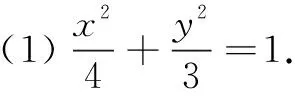
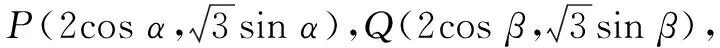
纵观连续三年的高考题,都涉及到直线与圆锥曲线位置关系的综合问题.笔者另辟蹊径,从两个方面应用参数方程巧解高考题,一是符合直线参数方程的条件时用直线的参数方程求解;二是不符合直线参数方程的条件时用圆锥曲线的参数方程求解.不管那种方法,都能简化解题过程,达到意想不到的效果.