运用向量的投影解题

李文东

(广东省中山市中山纪念中学，528454)

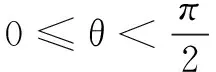
一、用投影求数量积

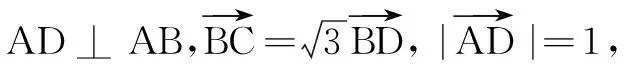
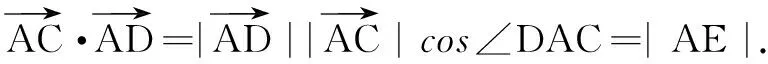
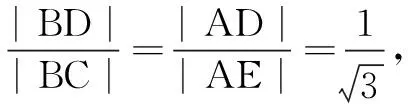
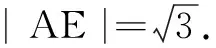
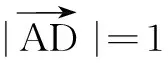
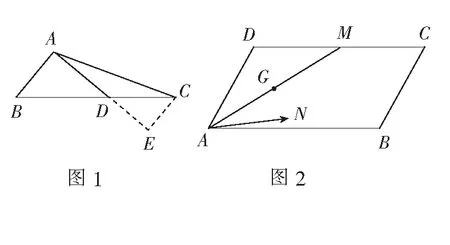
例2在ABCD中,点M为DC的中点,点N满足则______.

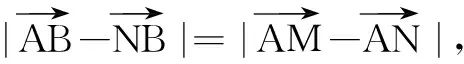
下面一例是这个重要结论的应用.

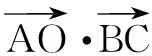
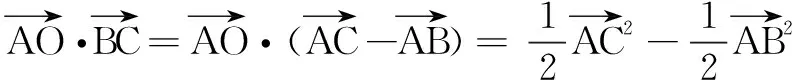
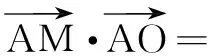
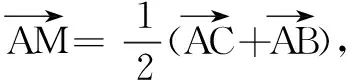
二、用投影求数量积的范围

例4已知正六边形P1P2P3P4P5P6(如图3),下列向量的数量积中最大的是( )

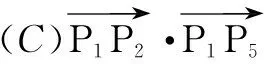
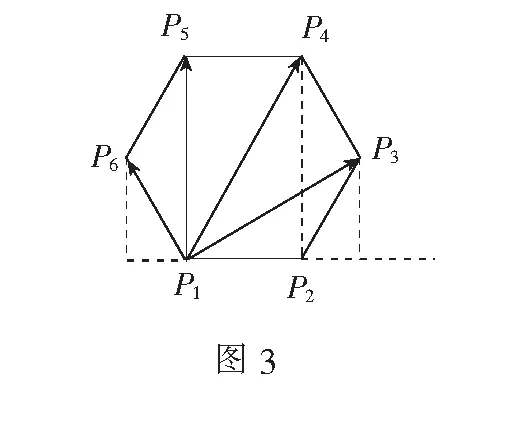
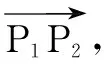
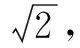
(A)[0,4] (B)[1,4]

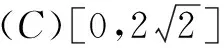
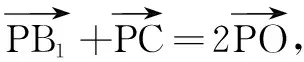
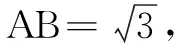
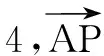
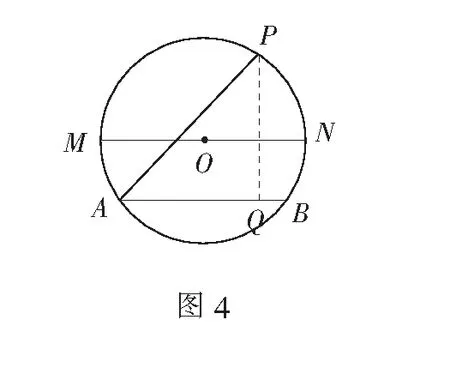
三、用投影求参数的值或取值范围

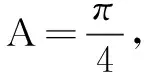
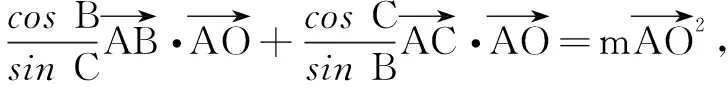
评注本题是一道难度极大的向量综合题,一般解法十分复杂.而借助于第一部分中的重要结论顺利求解,解法十分简洁漂亮!再如下面的例8.

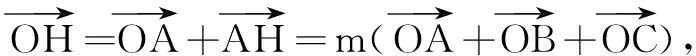
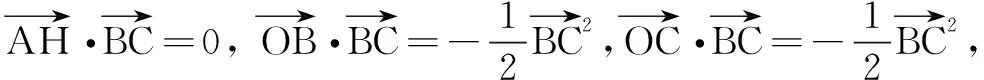
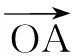
解由条件，可得

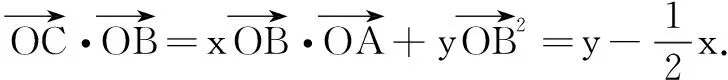
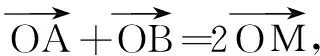
评注本题解法很多,这里借助投影求解,以形助数解法直观简捷.

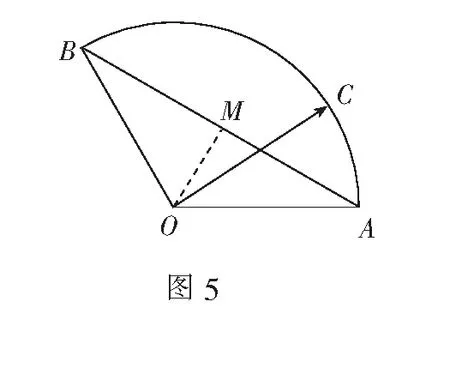
四、用投影求函数最值

例10已知x,y满足不等式组x+2y-1≥0，x-y+2≥0，2x+y-5≤0,求z=3x-2y的最大值.

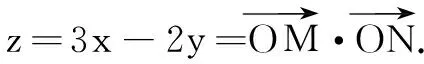
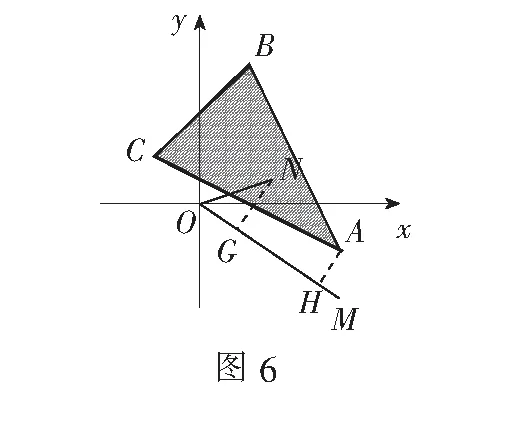
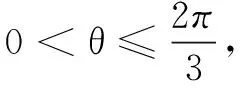
解设a=(cosθ,sinθ),b=(4,3),则f(θ)=a·b=5cos〈a，b〉，其中cos〈a·b〉表示a在b方向上的投影.

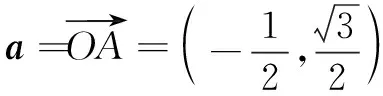
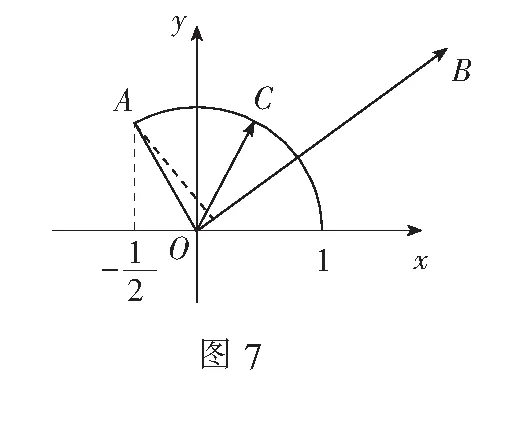
综上所述,在一些和向量数量积(或者能够转化为向量数量积)有关的问题中,如果我们能够从投影的角度去思考问题,有时会给我们带来意想不到的效果,这也是培养学生发散思维的一个很好的途径.